|
Surface Bundle Over The Circle
In mathematics, a surface bundle over the circle is a fiber bundle with base space a circle, and with fiber space a surface. Therefore the total space has dimension 2 + 1 = 3. In general, fiber bundles over the circle are a special case of mapping tori. Here is the construction: take the Cartesian product of a surface with the unit interval. Glue the two copies of the surface, on the boundary, by some homeomorphism. This homeomorphism is called the monodromy of the surface bundle. It is possible to show that the homeomorphism type of the bundle obtained depends only on the conjugacy class, in the mapping class group, of the gluing homeomorphism chosen. This construction is an important source of examples both in the field of low-dimensional topology as well as in geometric group theory. In the former we find that the geometry of the three-manifold is determined by the dynamics of the homeomorphism. This is the fibered part of William Thurston's geometrization theorem for Ha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
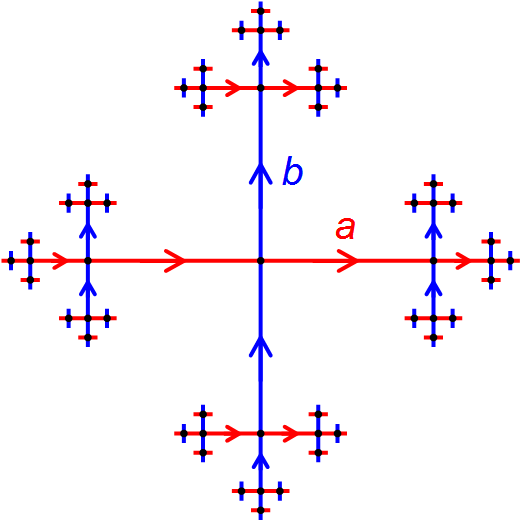
Geometric Group Theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such group (mathematics), groups and topology, topological and geometry, geometric properties of spaces on which these groups Group action (mathematics), act (that is, when the groups in question are realized as geometric symmetries or continuous transformations of some spaces). Another important idea in geometric group theory is to consider finitely generated groups themselves as geometric objects. This is usually done by studying the Cayley graphs of groups, which, in addition to the graph (discrete mathematics), graph structure, are endowed with the structure of a metric space, given by the so-called word metric. Geometric group theory, as a distinct area, is relatively new, and became a clearly identifiable branch of mathematics in the late 1980s and early 1990s. Geometric group theory closely interacts with low-dimens ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Virtually Fibered Conjecture
In the mathematical subfield of 3-manifolds, the virtually fibered conjecture, formulated by American mathematician William Thurston, states that every closed, irreducible, atoroidal 3-manifold with infinite fundamental group has a finite cover which is a surface bundle over the circle. A 3-manifold which has such a finite cover is said to virtually fiber. If ''M'' is a Seifert fiber space, then ''M'' virtually fibers if and only if the rational Euler number of the Seifert fibration or the (orbifold) Euler characteristic of the base space is zero. The hypotheses of the conjecture are satisfied by hyperbolic 3-manifolds. In fact, given that the geometrization conjecture is now settled, the only case needed to be proven for the virtually fibered conjecture is that of hyperbolic 3-manifolds. The original interest in the virtually fibered conjecture (as well as its weaker cousins, such as the virtually Haken conjecture) stemmed from the fact that any of these conjectures, combined w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torus Bundle
A torus bundle, in the sub-field of geometric topology in mathematics, is a kind of surface bundle over the circle, which in turn is a class of three-manifolds. Construction To obtain a torus bundle: let f be an orientation-preserving homeomorphism of the two-dimensional torus T to itself. Then the three-manifold M(f) is obtained by * taking the Cartesian product of T and the unit interval and * gluing one component of the boundary of the resulting manifold to the other boundary component via the map f. Then M(f) is the torus bundle with monodromy f. Examples For example, if f is the identity map (i.e., the map which fixes every point of the torus) then the resulting torus bundle M(f) is the three-torus: the Cartesian product of three circles. Seeing the possible kinds of torus bundles in more detail requires an understanding of William Thurston's geometrization program. Briefly, if f is finite order, then the manifold M(f) has Euclidean geometry. If f is a power of a De ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Henri Poincaré
Jules Henri Poincaré ( S: stress final syllable ; 29 April 1854 – 17 July 1912) was a French mathematician, theoretical physicist, engineer, and philosopher of science. He is often described as a polymath, and in mathematics as "The Last Universalist", since he excelled in all fields of the discipline as it existed during his lifetime. As a mathematician and physicist, he made many original fundamental contributions to pure and applied mathematics, mathematical physics, and celestial mechanics. In his research on the three-body problem, Poincaré became the first person to discover a chaotic deterministic system which laid the foundations of modern chaos theory. He is also considered to be one of the founders of the field of topology. Poincaré made clear the importance of paying attention to the invariance of laws of physics under different transformations, and was the first to present the Lorentz transformations in their modern symmetrical form. Poincaré discove ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
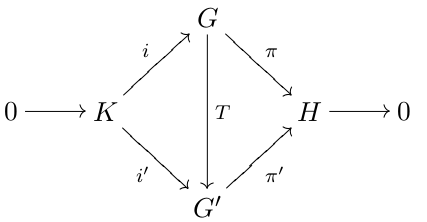
Group Extension
In mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence :1\to N\;\overset\;G\;\overset\;Q \to 1. If G is an extension of Q by N, then G is a group, \iota(N) is a normal subgroup of G and the quotient group G/\iota(N) is isomorphic to the group Q. Group extensions arise in the context of the extension problem, where the groups Q and N are known and the properties of G are to be determined. Note that the phrasing "G is an extension of N by Q" is also used by some. Since any finite group G possesses a maximal normal subgroup N with simple factor group G/N, all finite groups may be constructed as a series of extensions with finite simple groups. This fact was a motivation for completing the classification of finite simple groups. An extension is called a central extension if the subgroup N lies in the center o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
HNN-extension
In mathematics, the HNN extension is an important construction of combinatorial group theory. Introduced in a 1949 paper ''Embedding Theorems for Groups'' by Graham Higman, Bernhard Neumann, and Hanna Neumann, it embeds a given group ''G'' into another group ''G' '', in such a way that two given isomorphic subgroups of ''G'' are conjugate (through a given isomorphism) in ''G' ''. Construction Let ''G'' be a group with presentation G = \langle S \mid R\rangle , and let \alpha\colon H \to K be an isomorphism between two subgroups of ''G''. Let ''t'' be a new symbol not in ''S'', and define :G*_ = \left \langle S,t \mid R, tht^=\alpha(h), \forall h\in H \right \rangle. The group G*_ is called the ''HNN extension of'' ''G'' ''relative to'' α. The original group G is called the ''base group'' for the construction, while the subgroups ''H'' and ''K'' are the ''associated subgroups''. The new generator ''t'' is called the ''stable letter''. Key properties Since the presentation for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fundamental Group
In the mathematical field of algebraic topology, the fundamental group of a topological space is the group of the equivalence classes under homotopy of the loops contained in the space. It records information about the basic shape, or holes, of the topological space. The fundamental group is the first and simplest homotopy group. The fundamental group is a homotopy invariant—topological spaces that are homotopy equivalent (or the stronger case of homeomorphic) have isomorphic fundamental groups. The fundamental group of a topological space X is denoted by \pi_1(X). Intuition Start with a space (for example, a surface), and some point in it, and all the loops both starting and ending at this point— paths that start at this point, wander around and eventually return to the starting point. Two loops can be combined in an obvious way: travel along the first loop, then along the second. Two loops are considered equivalent if one can be deformed into the other without breakin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kleinian Group
In mathematics, a Kleinian group is a discrete subgroup of the group (mathematics), group of orientation-preserving Isometry, isometries of hyperbolic 3-space . The latter, identifiable with PSL(2,C), , is the quotient group of the 2 by 2 complex number, complex matrix (mathematics), matrices of determinant 1 by their center (group theory), center, which consists of the identity matrix and its product by . has a natural representation as orientation-preserving conformal transformations of the Riemann sphere, and as orientation-preserving conformal transformations of the open unit ball in . The group of Möbius transformation, Möbius transformations is also related as the non-orientation-preserving isometry group of , . So, a Kleinian group can be regarded as a discrete subgroup group action, acting on one of these spaces. History The theory of general Kleinian groups was founded by and , who named them after Felix Klein. The special case of Schottky groups had been studied a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nielsen–Thurston Classification
In mathematics, Thurston's classification theorem characterizes homeomorphisms of a compact orientable surface. William Thurston's theorem completes the work initiated by . Given a homeomorphism ''f'' : ''S'' → ''S'', there is a map ''g'' isotopic to ''f'' such that at least one of the following holds: * ''g'' is periodic, i.e. some power of ''g'' is the identity; * ''g'' preserves some finite union of disjoint simple closed curves on ''S'' (in this case, ''g'' is called ''reducible''); or * ''g'' is pseudo-Anosov. The case where ''S'' is a torus (i.e., a surface whose genus is one) is handled separately (see torus bundle) and was known before Thurston's work. If the genus of ''S'' is two or greater, then ''S'' is naturally hyperbolic, and the tools of Teichmüller theory become useful. In what follows, we assume ''S'' has genus at least two, as this is the case Thurston considered. (Note, however, that the cases where ''S'' has boundary or is not orienta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
William Thurston
William Paul Thurston (October 30, 1946August 21, 2012) was an American mathematician. He was a pioneer in the field of low-dimensional topology and was awarded the Fields Medal in 1982 for his contributions to the study of 3-manifolds. Thurston was a professor of mathematics at Princeton University, University of California, Davis, and Cornell University. He was also a director of the Mathematical Sciences Research Institute. Early life and education William Thurston was born in Washington, D.C. to Margaret Thurston (), a seamstress, and Paul Thurston, an aeronautical engineer. William Thurston suffered from congenital strabismus as a child, causing issues with depth perception. His mother worked with him as a toddler to reconstruct three-dimensional images from two-dimensional ones. He received his bachelor's degree from New College in 1967 as part of its inaugural class. For his undergraduate thesis, he developed an intuitionist foundation for topology. Following this, he r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geometries ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |