|
Stationary Random Measure
In probability theory, a random measure is a measure-valued random element. Random measures are for example used in the theory of random processes, where they form many important point processes such as Poisson point processes and Cox processes. Definition Random measures can be defined as transition kernels or as random elements. Both definitions are equivalent. For the definitions, let E be a separable complete metric space and let \mathcal E be its Borel \sigma -algebra. (The most common example of a separable complete metric space is \R^n ) As a transition kernel A random measure \zeta is a ( a.s.) locally finite transition kernel from a (abstract) probability space (\Omega, \mathcal A, P) to (E, \mathcal E) . Being a transition kernel means that *For any fixed B \in \mathcal \mathcal E , the mapping : \omega \mapsto \zeta(\omega,B) :is measurable from (\Omega, \mathcal A) to (E, \mathcal E) *For every fixed \omega \in \Omega , the mapping : B \mapsto \z ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Theory
Probability theory is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes (which provide mathematical abstractions of non-deterministic or uncertain processes or measured quantities that may either be single occurrences or evolve over time in a random fashion). Although it is not possible to perfectly predict random events, much can be said about their behavior. Two major results in probability ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Markov Kernel
In probability theory, a Markov kernel (also known as a stochastic kernel or probability kernel) is a map that in the general theory of Markov processes plays the role that the transition matrix does in the theory of Markov processes with a finite state space. Formal definition Let (X,\mathcal A) and (Y,\mathcal B) be measurable spaces. A ''Markov kernel'' with source (X,\mathcal A) and target (Y,\mathcal B) is a map \kappa : \mathcal B \times X \to ,1/math> with the following properties: # For every (fixed) B \in \mathcal B, the map x \mapsto \kappa(B, x) is \mathcal A-measurable # For every (fixed) x \in X, the map B \mapsto \kappa(B, x) is a probability measure on (Y, \mathcal B) In other words it associates to each point x \in X a probability measure \kappa(dy, x): B \mapsto \kappa(B, x) on (Y,\mathcal B) such that, for every measurable set B\in\mathcal B, the map x\mapsto \kappa(B, x) is measurable with respect to the \sigma-algebra \mathcal A. Examples Simple ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Measure
In mathematics, a vector measure is a function defined on a family of sets and taking vector values satisfying certain properties. It is a generalization of the concept of finite measure, which takes nonnegative real values only. Definitions and first consequences Given a field of sets (\Omega, \mathcal F) and a Banach space X, a finitely additive vector measure (or measure, for short) is a function \mu:\mathcal \to X such that for any two disjoint sets A and B in \mathcal one has \mu(A\cup B) =\mu(A) + \mu (B). A vector measure \mu is called countably additive if for any sequence (A_i)_^ of disjoint sets in \mathcal F such that their union is in \mathcal F it holds that \mu = \sum_^\mu(A_i) with the series on the right-hand side convergent in the norm of the Banach space X. It can be proved that an additive vector measure \mu is countably additive if and only if for any sequence (A_i)_^ as above one has where \, \cdot\, is the norm on X. Countably additive vector measur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poisson Random Measure
Let (E, \mathcal A, \mu) be some measure space with \sigma-finite measure \mu. The Poisson random measure with intensity measure \mu is a family of random variables \_ defined on some probability space (\Omega, \mathcal F, \mathrm) such that i) \forall A\in\mathcal,\quad N_A is a Poisson random variable with rate \mu(A). ii) If sets A_1,A_2,\ldots,A_n\in\mathcal don't intersect then the corresponding random variables from i) are mutually independent. iii) \forall\omega\in\Omega\;N_(\omega) is a measure on (E, \mathcal ) Existence If \mu\equiv 0 then N\equiv 0 satisfies the conditions i)–iii). Otherwise, in the case of finite measure \mu, given Z, a Poisson random variable with rate \mu(E), and X_, X_,\ldots, mutually independent random variables with distribution \frac, define N_(\omega) = \sum\limits_^ \delta_(\cdot) where \delta_(A) is a degenerate measure located in c. Then N will be a Poisson random measure. In the case \mu is not finite the measure N can be obtai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Particle Filter
Particle filters, or sequential Monte Carlo methods, are a set of Monte Carlo algorithms used to solve filtering problems arising in signal processing and Bayesian statistical inference. The filtering problem consists of estimating the internal states in dynamical systems when partial observations are made and random perturbations are present in the sensors as well as in the dynamical system. The objective is to compute the posterior distributions of the states of a Markov process, given the noisy and partial observations. The term "particle filters" was first coined in 1996 by Del Moral about mean-field interacting particle methods used in fluid mechanics since the beginning of the 1960s. The term "Sequential Monte Carlo" was coined by Liu and Chen in 1998. Particle filtering uses a set of particles (also called samples) to represent the posterior distribution of a stochastic process given the noisy and/or partial observations. The state-space model can be nonlinear and t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Quadrature
In analysis, numerical integration comprises a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of definite integrals. The term numerical quadrature (often abbreviated to ''quadrature'') is more or less a synonym for ''numerical integration'', especially as applied to one-dimensional integrals. Some authors refer to numerical integration over more than one dimension as cubature; others take ''quadrature'' to include higher-dimensional integration. The basic problem in numerical integration is to compute an approximate solution to a definite integral :\int_a^b f(x) \, dx to a given degree of accuracy. If is a smooth function integrated over a small number of dimensions, and the domain of integration is bounded, there are many methods for approximating the integral to the desired precision. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
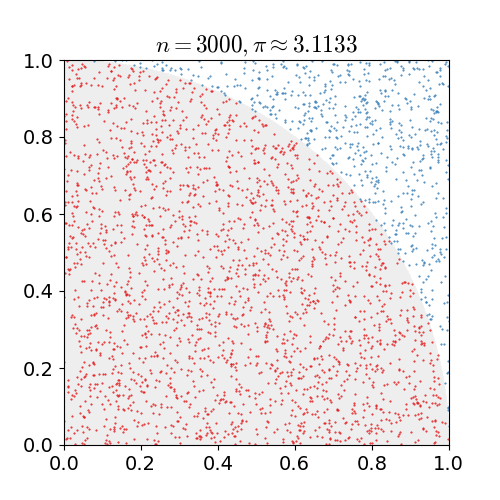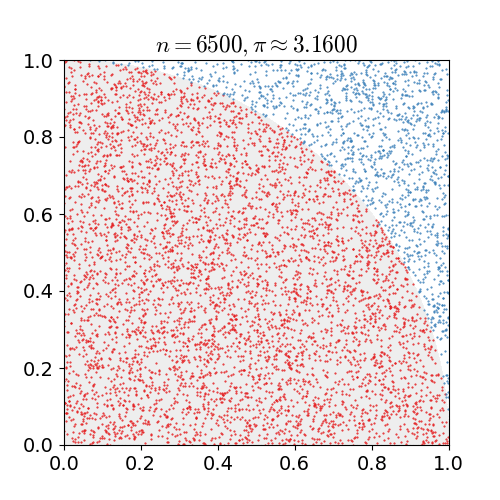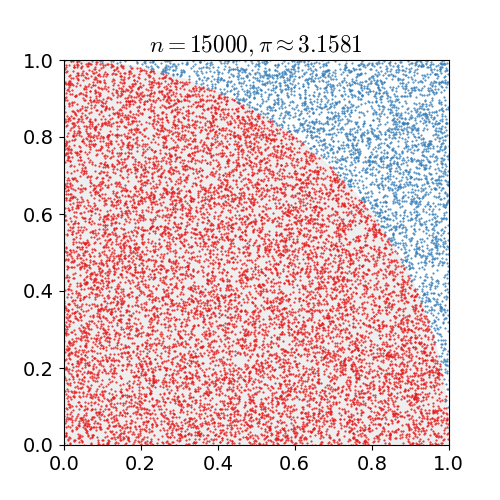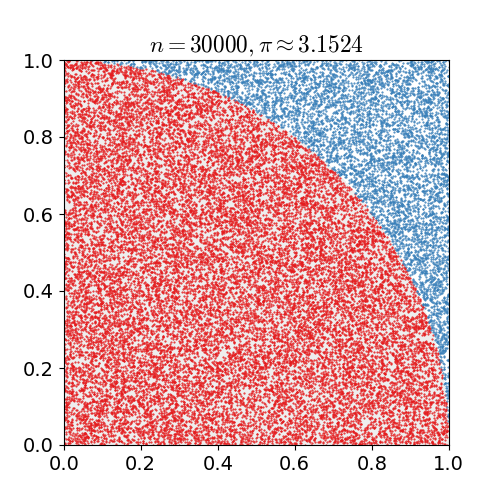
Monte Carlo Method
Monte Carlo methods, or Monte Carlo experiments, are a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results. The underlying concept is to use randomness to solve problems that might be deterministic in principle. They are often used in physical and mathematical problems and are most useful when it is difficult or impossible to use other approaches. Monte Carlo methods are mainly used in three problem classes: optimization, numerical integration, and generating draws from a probability distribution. In physics-related problems, Monte Carlo methods are useful for simulating systems with many coupled degrees of freedom, such as fluids, disordered materials, strongly coupled solids, and cellular structures (see cellular Potts model, interacting particle systems, McKean–Vlasov processes, kinetic models of gases). Other examples include modeling phenomena with significant uncertainty in inputs such as the calculation of ris ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Measurable Space
In mathematics, a measurable space or Borel space is a basic object in measure theory. It consists of a set and a σ-algebra, which defines the subsets that will be measured. Definition Consider a set X and a σ-algebra \mathcal A on X. Then the tuple (X, \mathcal A) is called a measurable space. Note that in contrast to a measure space, no measure is needed for a measurable space. Example Look at the set: X = \. One possible \sigma-algebra would be: \mathcal A_1 = \. Then \left(X, \mathcal A_1\right) is a measurable space. Another possible \sigma-algebra would be the power set on X: \mathcal A_2 = \mathcal P(X). With this, a second measurable space on the set X is given by \left(X, \mathcal A_2\right). Common measurable spaces If X is finite or countably infinite, the \sigma-algebra is most often the power set on X, so \mathcal A = \mathcal P(X). This leads to the measurable space (X, \mathcal P(X)). If X is a topological space In mathematics, a topological space is, rou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Counting Measure
In common usage, randomness is the apparent or actual lack of pattern or predictability in events. A random sequence of events, symbols or steps often has no order and does not follow an intelligible pattern or combination. Individual random events are, by definition, unpredictable, but if the probability distribution is known, the frequency of different outcomes over repeated events (or "trials") is predictable.Strictly speaking, the frequency of an outcome will converge almost surely to a predictable value as the number of trials becomes arbitrarily large. Non-convergence or convergence to a different value is possible, but has probability zero. For example, when throwing two dice, the outcome of any particular roll is unpredictable, but a sum of 7 will tend to occur twice as often as 4. In this view, randomness is not haphazardness; it is a measure of uncertainty of an outcome. Randomness applies to concepts of chance, probability, and information entropy. The fields ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirac Measure
In mathematics, a Dirac measure assigns a size to a set based solely on whether it contains a fixed element ''x'' or not. It is one way of formalizing the idea of the Dirac delta function, an important tool in physics and other technical fields. Definition A Dirac measure is a measure on a set (with any -algebra of subsets of ) defined for a given and any (measurable) set by :\delta_x (A) = 1_A(x)= \begin 0, & x \not \in A; \\ 1, & x \in A. \end where is the indicator function of . The Dirac measure is a probability measure, and in terms of probability it represents the almost sure outcome in the sample space . We can also say that the measure is a single atom at ; however, treating the Dirac measure as an atomic measure is not correct when we consider the sequential definition of Dirac delta, as the limit of a delta sequence. The Dirac measures are the extreme points of the convex set of probability measures on . The name is a back-formation from the Dirac delta fun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simple Function
In the mathematical field of real analysis, a simple function is a real (or complex)-valued function over a subset of the real line, similar to a step function. Simple functions are sufficiently "nice" that using them makes mathematical reasoning, theory, and proof easier. For example, simple functions attain only a finite number of values. Some authors also require simple functions to be measurable; as used in practice, they invariably are. A basic example of a simple function is the floor function over the half-open interval , 9), whose only values are . A more advanced example is the Dirichlet function over the real line, which takes the value 1 if ''x'' is rational and 0 otherwise. (Thus the "simple" of "simple function" has a technical meaning somewhat at odds with common language.) All step functions are simple. Simple functions are used as a first stage in the development of theories of integral">integration, such as the Lebesgue integral, because it is easy to define inte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semiring
In abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse. The term rig is also used occasionally—this originated as a joke, suggesting that rigs are ri''n''gs without ''n''egative elements, similar to using '' rng'' to mean a r''i''ng without a multiplicative ''i''dentity. Tropical semirings are an active area of research, linking algebraic varieties with piecewise linear structures. Definition A semiring is a set R equipped with two binary operations \,+\, and \,\cdot,\, called addition and multiplication, such that:Lothaire (2005) p.211Sakarovitch (2009) pp.27–28 * (R, +) is a commutative monoid with identity element 0: ** (a + b) + c = a + (b + c) ** 0 + a = a = a + 0 ** a + b = b + a * (R, \,\cdot\,) is a monoid with identity element 1: ** (a \cdot b) \cdot c = a \cdot (b \cdot c) ** 1 \cdot a = a = a \cdot 1 * Multiplication left and right distributes over addition: * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |