|
Self-financing Portfolio
In financial mathematics, a self-financing portfolio is a portfolio having the feature that, if there is no exogenous infusion or withdrawal of money, the purchase of a new asset must be financed by the sale of an old one. This concept is used to define for example admissible strategies and replicating portfolios, the latter being fundamental for arbitrage-free derivative pricing. Mathematical definition Discrete time Assume we are given a discrete filtered probability space (\Omega,\mathcal,\_^T,P), and let K_t be the solvency cone (with or without transaction costs) at time ''t'' for the market. Denote by L_d^p(K_t) = \. Then a portfolio (H_t)_^T (in physical units, i.e. the number of each stock) is self-financing (with trading on a finite set of times only) if : for all t \in \ we have that H_t - H_ \in -K_t \; P-a.s. with the convention that H_ = 0. If we are only concerned with the set that the portfolio can be at some future time then we can say that H_ \in -K_0 - ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Financial Mathematics
Mathematical finance, also known as quantitative finance and financial mathematics, is a field of applied mathematics, concerned with mathematical modeling in the Finance#Quantitative_finance, financial field. In general, there exist two separate branches of finance that require advanced quantitative techniques: Derivative (finance), derivatives pricing on the one hand, and risk management, risk and Investment management#Investment managers and portfolio structures, portfolio management on the other. Mathematical finance overlaps heavily with the fields of computational finance and financial engineering. The latter focuses on applications and modeling, often with the help of stochastic asset models, while the former focuses, in addition to analysis, on building tools of implementation for the models. Also related is quantitative investing, which relies on statistical and numerical models (and lately machine learning) as opposed to traditional fundamental analysis when investment ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Portfolio (finance)
In finance, a portfolio is a collection of investments. Definition The term "portfolio" refers to any combination of financial assets such as stocks, bonds and cash. Portfolios may be held by individual investors or managed by financial professionals, hedge funds, banks and other financial institutions. It is a generally accepted principle that a portfolio is designed according to the investor's risk tolerance, time frame and investment objectives. The monetary value of each asset may influence the risk/reward ratio of the portfolio. When determining asset allocation, the aim is to maximise the expected return and minimise the risk. This is an example of a multi-objective optimization problem: many efficient solutions are available and the preferred solution must be selected by considering a tradeoff between risk and return. In particular, a portfolio A is dominated by another portfolio A' if A' has a greater expected gain and a lesser risk than A. If no portfolio dominates A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Admissible Trading Strategy
In finance, an admissible trading strategy or admissible strategy is any trading strategy with wealth almost surely bounded from below. In particular, an admissible trading strategy precludes unhedged short sales of any unbounded assets. A typical example of a trading strategy which is not ''admissible'' is the doubling strategy. Mathematical definition Discrete time In a market with d assets, a trading strategy x \in \mathbb^d is ''admissible'' if x^T \bar = x^T \frac is almost surely bounded from below. In the definition let S be the vector of prices, r be the risk-free rate (and therefore \bar is the discounted price). In a model with more than one time then the wealth process associated with an admissible trading strategy must be uniformly bounded from below. Continuous time Let S=(S_t)_ be a d-dimensional semimartingale market and H=(H_t)_ a predictable stochastic process/trading strategy. Then H is called ''admissible integrand for the semimartingale'' S or just ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Replicating Portfolio
In mathematical finance, a replicating portfolio for a given asset or series of cash flows is a portfolio of assets with the same properties (especially cash flows). This is meant in two distinct senses: static replication, where the portfolio has the same cash flows as the reference asset (and no changes need to be made to maintain this), and dynamic replication, where the portfolio does not have the same cash flows, but has the same "Greeks" as the reference asset, meaning that for small (properly, infinitesimal) changes to underlying market parameters, the price of the asset and the price of the portfolio change in the same way. Dynamic replication requires continual adjustment, as the asset and portfolio are only assumed to behave similarly at a single point (mathematically, their partial derivatives are equal at a single point). Given an asset or liability, an offsetting replicating portfolio (a " hedge") is called a static hedge or dynamic hedge, and constructing such a portf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Rational Pricing
Rational pricing is the assumption in financial economics that asset prices – and hence asset pricing models – will reflect the arbitrage-free price of the asset as any deviation from this price will be "arbitraged away". This assumption is useful in pricing fixed income securities, particularly bonds, and is fundamental to the pricing of derivative instruments. Arbitrage mechanics Arbitrage is the practice of taking advantage of a state of imbalance between two (or possibly more) markets. Where this mismatch can be exploited (i.e. after transaction costs, storage costs, transport costs, dividends etc.) the arbitrageur can "lock in" a risk-free profit by purchasing and selling simultaneously in both markets. In general, arbitrage ensures that "the law of one price" will hold; arbitrage also equalises the prices of assets with identical cash flows, and sets the price of assets with known future cash flows. The law of one price The same asset must trade at the same ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Filtered Probability Space
In the theory of stochastic processes, a subdiscipline of probability theory, filtrations are totally ordered collections of subsets that are used to model the information that is available at a given point and therefore play an important role in the formalization of random (stochastic) processes. Definition Let (\Omega, \mathcal A, P) be a probability space and let I be an index set with a total order \leq (often \N , \R^+ , or a subset of \mathbb R^+ ). For every i \in I let \mathcal F_i be a sub-''σ''-algebra of \mathcal A . Then : \mathbb F:= (\mathcal F_i)_ is called a filtration, if \mathcal F_k \subseteq \mathcal F_\ell for all k \leq \ell . So filtrations are families of ''σ''-algebras that are ordered non-decreasingly. If \mathbb F is a filtration, then (\Omega, \mathcal A, \mathbb F, P) is called a filtered probability space. Example Let (X_n)_ be a stochastic process on the probability space (\Omega, \mathcal A, P) . Let \sigma(X_k ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
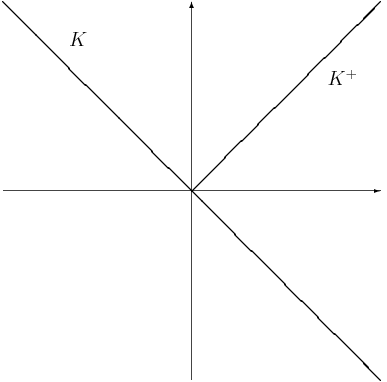
Solvency Cone
The solvency cone is a concept used in financial mathematics which models the possible trades in the financial market. This is of particular interest to markets with transaction costs. Specifically, it is the convex cone of portfolios that can be exchanged to portfolios of non-negative components (including paying of any transaction costs). Mathematical basis If given a bid-ask matrix \Pi for d assets such that \Pi = \left(\pi^\right)_ and m \leq d is the number of assets which with any non-negative quantity of them can be "discarded" (traditionally m = d), then the solvency cone K(\Pi) \subset \mathbb^d is the convex cone spanned by the unit vectors e^i, 1 \leq i \leq m and the vectors \pi^e^i-e^j, 1 \leq i,j \leq d. Definition A solvency cone K is any closed convex cone such that K \subseteq \mathbb^d and K \supseteq \mathbb^d_+. Uses A process of (random) solvency cones \left\_^T is a model of a financial market. This is sometimes called a market process. The negative of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Transaction Costs
In economics, a transaction cost is a cost incurred when making an economic trade when participating in a market. The idea that transactions form the basis of economic thinking was introduced by the institutional economist John R. Commons in 1931. Oliver E. Williamson's ''Transaction Cost Economics'' article, published in 2008, popularized the concept of transaction costs. Douglass C. North argues that institutions, understood as the set of rules in a society, are key in the determination of transaction costs. In this sense, institutions that facilitate low transaction costs can boost economic growth.North, Douglass C. 1992. "Transaction costs, institutions, and economic performance", San Francisco, CA: ICS Press. Alongside production costs, transaction costs are one of the most significant factors in business operation and management. Definition Williamson defines transaction costs as a cost innate in running an economic system of companies, comprising the total costs of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Semimartingale
In probability theory, a real-valued stochastic process ''X'' is called a semimartingale if it can be decomposed as the sum of a local martingale and a càdlàg adapted finite-variation process. Semimartingales are "good integrators", forming the largest class of processes with respect to which the Itô integral and the Stratonovich integral can be defined. The class of semimartingales is quite large (including, for example, all continuously differentiable processes, Brownian motion and Poisson processes). Submartingales and supermartingales together represent a subset of the semimartingales. Definition A real-valued process ''X'' defined on the filtered probability space (Ω,''F'',(''F''''t'')''t'' ≥ 0,P) is called a semimartingale if it can be decomposed as :X_t = M_t + A_t where ''M'' is a local martingale and ''A'' is a càdlàg adapted process of locally bounded variation. This means that for almost all \omega \in \Omega and all compact intervals ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Frictionless Market
In economic theory a frictionless market is a financial market without transaction costs. Friction is a type of market incompleteness. Every complete market is frictionless, but the converse does not hold. In a frictionless market the solvency cone is the halfspace normal to the unique price vector. The Black–Scholes model The Black–Scholes or Black–Scholes–Merton model is a mathematical model for the dynamics of a financial market containing Derivative (finance), derivative investment instruments. From the parabolic partial differential equation in the model, ... assumes a frictionless market. References Financial markets Mathematical finance {{finance-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Itô Calculus
Itô calculus, named after Kiyosi Itô, extends the methods of calculus to stochastic processes such as Brownian motion (see Wiener process). It has important applications in mathematical finance and stochastic differential equations. The central concept is the Itô stochastic integral, a stochastic generalization of the Riemann–Stieltjes integral in analysis. The integrands and the integrators are now stochastic processes: Y_t = \int_0^t H_s\,dX_s, where is a locally square-integrable process adapted to the filtration generated by , which is a Brownian motion or, more generally, a semimartingale. The result of the integration is then another stochastic process. Concretely, the integral from 0 to any particular is a random variable, defined as a limit of a certain sequence of random variables. The paths of Brownian motion fail to satisfy the requirements to be able to apply the standard techniques of calculus. So with the integrand a stochastic process, the Itô stochas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Self-financing
In the theory of capital structure, internal financing or self-financing is using its profits or assets of a company or organization as a source of capital to fund a new project or investment. Internal sources of finance contrast with external sources of finance. The main difference between the two is that internal financing refers to the business generating funds from activities and assets that already exist in the company whereas external financing requires the involvement of a third party. Internal financing is generally thought to be less expensive for the firm than external financing because the firm does not have to incur transaction costs to obtain it, nor does it have to pay the taxes associated with paying dividends. Many economists debate whether the availability of internal financing is an important determinant of firm investment or not. A related controversy is whether the fact that internal financing is empirically correlated with investment implies firms are credit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |