|
Support Vector Machines
In machine learning, support vector machines (SVMs, also support vector networks) are supervised learning models with associated learning algorithms that analyze data for classification and regression analysis. Developed at AT&T Bell Laboratories by Vladimir Vapnik with colleagues (Boser et al., 1992, Guyon et al., 1993, Cortes and Vapnik, 1995, Vapnik et al., 1997) SVMs are one of the most robust prediction methods, being based on statistical learning frameworks or VC theory proposed by Vapnik (1982, 1995) and Chervonenkis (1974). Given a set of training examples, each marked as belonging to one of two categories, an SVM training algorithm builds a model that assigns new examples to one category or the other, making it a non-probabilistic binary linear classifier (although methods such as Platt scaling exist to use SVM in a probabilistic classification setting). SVM maps training examples to points in space so as to maximise the width of the gap between the two categories. New ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Machine Learning
Machine learning (ML) is a field of inquiry devoted to understanding and building methods that 'learn', that is, methods that leverage data to improve performance on some set of tasks. It is seen as a part of artificial intelligence. Machine learning algorithms build a model based on sample data, known as training data, in order to make predictions or decisions without being explicitly programmed to do so. Machine learning algorithms are used in a wide variety of applications, such as in medicine, email filtering, speech recognition, agriculture, and computer vision, where it is difficult or unfeasible to develop conventional algorithms to perform the needed tasks.Hu, J.; Niu, H.; Carrasco, J.; Lennox, B.; Arvin, F.,Voronoi-Based Multi-Robot Autonomous Exploration in Unknown Environments via Deep Reinforcement Learning IEEE Transactions on Vehicular Technology, 2020. A subset of machine learning is closely related to computational statistics, which focuses on making pred ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hava Siegelmann
Hava Siegelmann is a professor of computer science. Her academic position is in the school of Computer Science and the Program of Neuroscience and Behavior at the University of Massachusetts Amherst; she is the director of the school's Biologically Inspired Neural and Dynamical Systems Lab and is the Provost Professor of the University of Massachusetts. She was loaned to the federal government DARPA 2016-2019 to initiate and run their most advanced AI programs including her Lifelong Learning Machine (L2M) program. and Guaranteeing AI Robustness against Deceptions (GARD). She received the rarely awarded Meritorious Public Service Medal — one of the highest honors the Department of Defense agency can bestow on a private citizen. Biography Siegelmann is an American computer scientist who founded the field of Super-Turing computation. As a DAPRA Program Manager she introduced the field of Lifelong Learning Machines, the most recent advancement in Artificial Intelligence, which is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positive-definite Kernel
In operator theory, a branch of mathematics, a positive-definite kernel is a generalization of a positive-definite function or a positive-definite matrix. It was first introduced by James Mercer in the early 20th century, in the context of solving integral operator equations. Since then, positive-definite functions and their various analogues and generalizations have arisen in diverse parts of mathematics. They occur naturally in Fourier analysis, probability theory, operator theory, complex function-theory, moment problems, integral equations, boundary-value problems for partial differential equations, machine learning, embedding problem, information theory, and other areas. This article will discuss some of the historical and current developments of the theory of positive-definite kernels, starting with the general idea and properties before considering practical applications. Definition Let \mathcal X be a nonempty set, sometimes referred to as the index set. A symme ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dot Product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a scalar as a result". It is also used sometimes for other symmetric bilinear forms, for example in a pseudo-Euclidean space. is an algebraic operation that takes two equal-length sequences of numbers (usually coordinate vectors), and returns a single number. In Euclidean geometry, the dot product of the Cartesian coordinates of two vectors is widely used. It is often called the inner product (or rarely projection product) of Euclidean space, even though it is not the only inner product that can be defined on Euclidean space (see Inner product space for more). Algebraically, the dot product is the sum of the products of the corresponding entries of the two sequences of numbers. Geometrically, it is the product of the Euclidean magnitudes of the two vectors and the cosine of the angle between them. These definitions are equivalent when using Cartesian coordinates. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Separability
In Euclidean geometry, linear separability is a property of two sets of point (geometry), points. This is most easily visualized in two dimensions (the Euclidean plane) by thinking of one set of points as being colored blue and the other set of points as being colored red. These two sets are ''linearly separable'' if there exists at least one line (geometry), line in the plane with all of the blue points on one side of the line and all the red points on the other side. This idea immediately generalizes to higher-dimensional Euclidean spaces if the line is replaced by a hyperplane. The problem of determining if a pair of sets is linearly separable and finding a separating hyperplane if they are, arises in several areas. In statistics and machine learning, classifying certain types of data is a problem for which good algorithms exist that are based on this concept. Mathematical definition Let X_ and X_ be two sets of points in an ''n''-dimensional Euclidean space. Then X_ and X_ ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kernel Machine
Kernel may refer to: Computing * Kernel (operating system), the central component of most operating systems * Kernel (image processing), a matrix used for image convolution * Compute kernel, in GPGPU programming * Kernel method, in machine learning * Kernelization, a technique for designing efficient algorithms ** Kernel, a routine that is executed in a vectorized loop, for example in general-purpose computing on graphics processing units *KERNAL, the Commodore operating system Mathematics Objects * Kernel (algebra), a general concept that includes: ** Kernel (linear algebra) or null space, a set of vectors mapped to the zero vector ** Kernel (category theory), a generalization of the kernel of a homomorphism ** Kernel (set theory), an equivalence relation: partition by image under a function ** Difference kernel, a binary equalizer: the kernel of the difference of two functions Functions * Kernel (geometry), the set of points within a polygon from which the whole polygon boundary ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
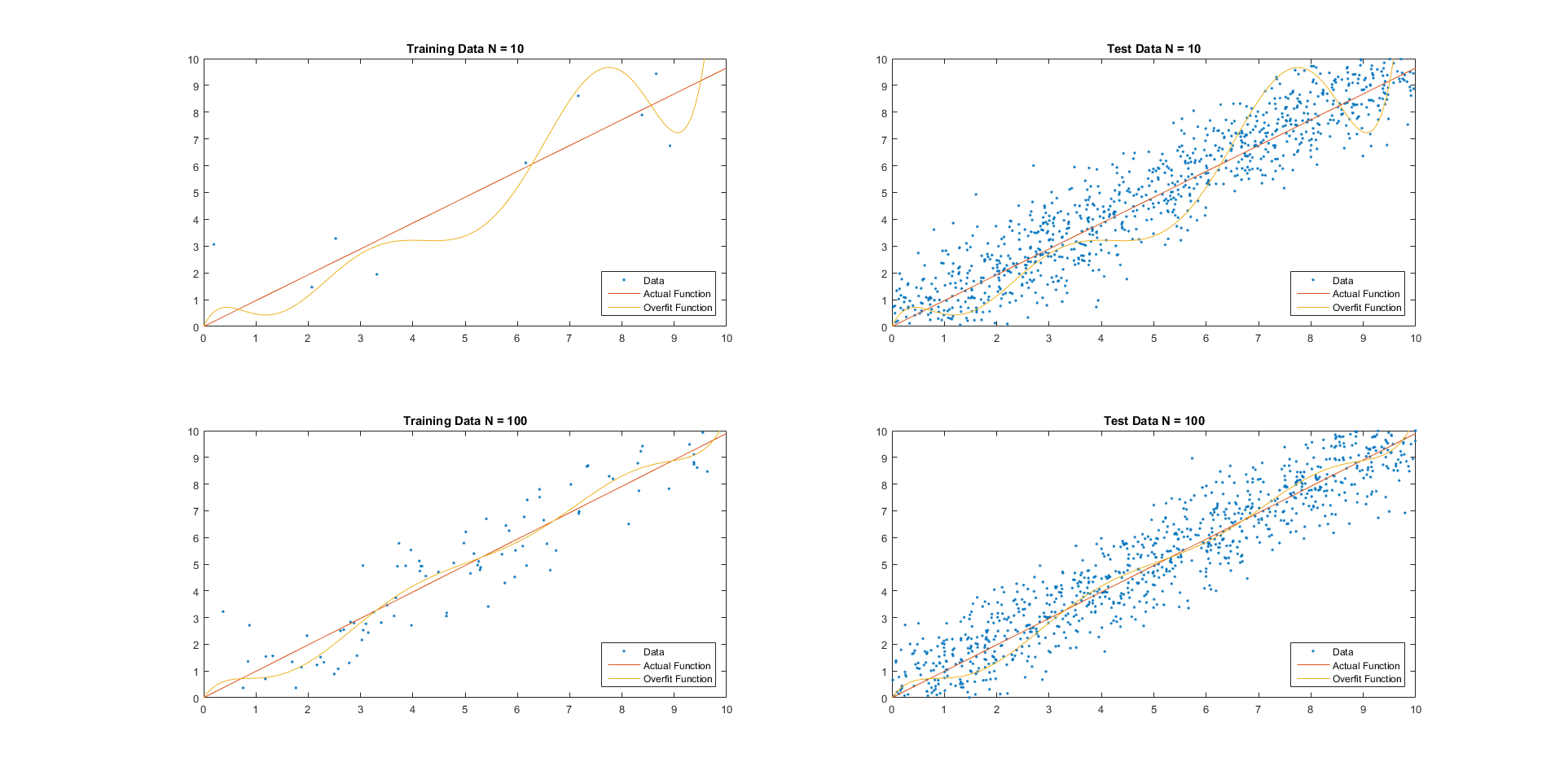
Generalization Error
For supervised learning applications in machine learning and statistical learning theory, generalization error (also known as the out-of-sample error or the risk) is a measure of how accurately an algorithm is able to predict outcome values for previously unseen data. Because learning algorithms are evaluated on finite samples, the evaluation of a learning algorithm may be sensitive to sampling error. As a result, measurements of prediction error on the current data may not provide much information about predictive ability on new data. Generalization error can be minimized by avoiding overfitting in the learning algorithm. The performance of a machine learning algorithm is visualized by plots that show values of ''estimates'' of the generalization error through the learning process, which are called learning curves. Definition In a learning problem, the goal is to develop a function f_n(\vec) that predicts output values y for each input datum \vec. The subscript n indicates that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
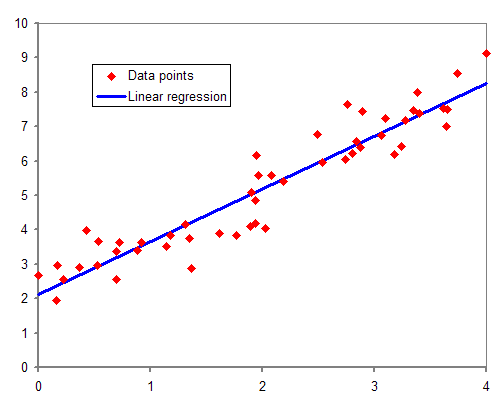
Regression Analysis
In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the 'outcome' or 'response' variable, or a 'label' in machine learning parlance) and one or more independent variables (often called 'predictors', 'covariates', 'explanatory variables' or 'features'). The most common form of regression analysis is linear regression, in which one finds the line (or a more complex linear combination) that most closely fits the data according to a specific mathematical criterion. For example, the method of ordinary least squares computes the unique line (or hyperplane) that minimizes the sum of squared differences between the true data and that line (or hyperplane). For specific mathematical reasons (see linear regression), this allows the researcher to estimate the conditional expectation (or population average value) of the dependent variable when the independent variables take on a given ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perceptron
In machine learning, the perceptron (or McCulloch-Pitts neuron) is an algorithm for supervised classification, supervised learning of binary classification, binary classifiers. A binary classifier is a function which can decide whether or not an input, represented by a vector of numbers, belongs to some specific class. It is a type of linear classifier, i.e. a classification algorithm that makes its predictions based on a linear predictor function combining a set of Weighting, weights with the feature vector. History The perceptron was invented in 1943 by McCulloch and Pitts. The first implementation was a machine built in 1958 at the Cornell Aeronautical Laboratory by Frank Rosenblatt, funded by the United States Office of Naval Research. The perceptron was intended to be a machine, rather than a program, and while its first implementation was in software for the IBM 704, it was subsequently implemented in custom-built hardware as the "Mark 1 perceptron". This machine was de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Margin Classifier
In machine learning, a margin classifier is a classifier which is able to give an associated distance from the decision boundary for each example. For instance, if a linear classifier (e.g. perceptron or linear discriminant analysis) is used, the distance (typically euclidean distance, though others may be used) of an example from the separating hyperplane is the margin of that example. The notion of margin is important in several machine learning classification algorithms, as it can be used to bound the generalization error of the classifier. These bounds are frequently shown using the VC dimension. Of particular prominence is the generalization error bound on boosting algorithms and support vector machines. Support vector machine definition of margin See support vector machines and maximum-margin hyperplane for details. Margin for boosting algorithms The margin for an iterative boosting algorithm given a set of examples with two classes can be defined as follows. The clas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maximum-margin Hyperplane
In geometry, the hyperplane separation theorem is a theorem about disjoint convex sets in ''n''-dimensional Euclidean space. There are several rather similar versions. In one version of the theorem, if both these sets are closed and at least one of them is compact, then there is a hyperplane in between them and even two parallel hyperplanes in between them separated by a gap. In another version, if both disjoint convex sets are open, then there is a hyperplane in between them, but not necessarily any gap. An axis which is orthogonal to a separating hyperplane is a separating axis, because the orthogonal projections of the convex bodies onto the axis are disjoint. The hyperplane separation theorem is due to Hermann Minkowski. The Hahn–Banach separation theorem generalizes the result to topological vector spaces. A related result is the supporting hyperplane theorem. In the context of support-vector machines, the ''optimally separating hyperplane'' or ''maximum-margin hyper ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Margin (machine Learning)
In machine learning the margin of a single data point is defined to be the distance from the data point to a decision boundary. Note that there are many distances and decision boundaries that may be appropriate for certain datasets and goals. A margin classifier is a classifier that explicitly utilizes the margin of each example while learning a classifier. There are theoretical justifications (based on the VC dimension) as to why maximizing the margin (under some suitable constraints) may be beneficial for machine learning and statistical inferences algorithms. There are many hyperplanes that might classify the data. One reasonable choice as the best hyperplane is the one that represents the largest separation, or margin, between the two classes. So we choose the hyperplane so that the distance from it to the nearest data point on each side is maximized. If such a hyperplane exists, it is known as the ''maximum-margin hyperplane'' and the linear classifier it defines is kno ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |