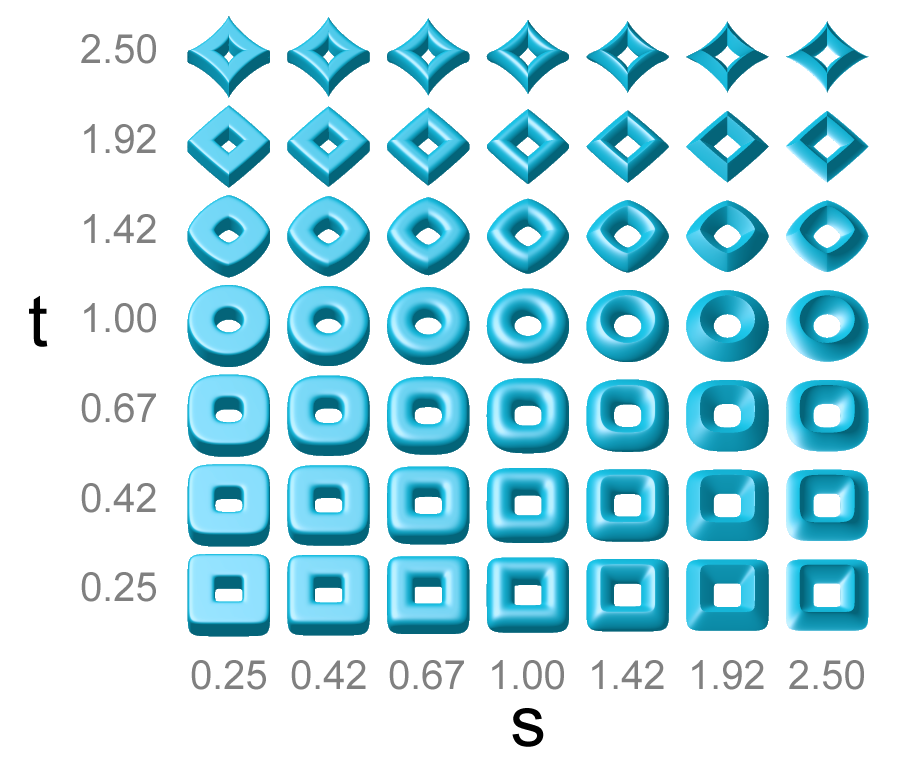
|
Superellipsoid
In mathematics, a superellipsoid (or super-ellipsoid) is a solid geometry, solid whose horizontal sections are superellipses (Lamé curves) with the same squareness parameter \epsilon_2, and whose vertical sections through the center are superellipses with the squareness parameter \epsilon_1. It is a generalization of an ellipsoid, which is a special case when \epsilon_1=\epsilon_2=1. Superellipsoids as computer graphics primitives were popularized by Alan H. Barr (who used the name "superquadrics" to refer to both superellipsoids and supertoroids).Barr, A.H. (1992), ''Rigid Physically Based Superquadrics''. Chapter III.8 of ''Graphics Gems III'', edited by D. Kirk, pp. 137–159 In modern computer vision and robotics literatures, superquadrics and superellipsoids are used interchangeably, since superellipsoids are the most representative and widely utilized shape among all the superquadrics. Superellipsoids have a rich shape vocabulary, including cuboids, cylinders, ellipso ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Superellipsoid Collection
In mathematics, a superellipsoid (or super-ellipsoid) is a solid whose horizontal sections are superellipses (Lamé curves) with the same squareness parameter \epsilon_2, and whose vertical sections through the center are superellipses with the squareness parameter \epsilon_1. It is a generalization of an ellipsoid, which is a special case when \epsilon_1=\epsilon_2=1. Superellipsoids as computer graphics primitives were popularized by Alan H. Barr (who used the name " superquadrics" to refer to both superellipsoids and supertoroids).Barr, A.H. (1992), ''Rigid Physically Based Superquadrics''. Chapter III.8 of ''Graphics Gems III'', edited by D. Kirk, pp. 137–159 In modern computer vision and robotics literatures, superquadrics and superellipsoids are used interchangeably, since superellipsoids are the most representative and widely utilized shape among all the superquadrics. Superellipsoids have a rich shape vocabulary, including cuboids, cylinders, ellipsoids, octahed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Superquadrics
In mathematics, the superquadrics or super-quadrics (also superquadratics) are a family of geometric shapes defined by formulas that resemble those of ellipsoids and other quadrics, except that the squaring operations are replaced by arbitrary powers. They can be seen as the three-dimensional relatives of the superellipses. The term may refer to the solid object or to its surface, depending on the context. The equations below specify the surface; the solid is specified by replacing the equality signs by less-than-or-equal signs. The superquadrics include many shapes that resemble cubes, octahedra, cylinders, lozenges and spindles, with rounded or sharp corners. Because of their flexibility and relative simplicity, they are popular geometric modeling tools, especially in computer graphics. It becomes an important geometric primitive widely used in computer vision, robotics, and physical simulation. Some authors, such as Alan Barr, define "superquadrics" as including both the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Supertoroid
In geometry and computer graphics, a supertoroid or supertorus is usually understood to be a family of doughnut-like surfaces (technically, a topological torus) whose shape is defined by mathematical formulas similar to those that define the superellipsoids. The plural of "supertorus" is either supertori or supertoruses. The family was described and named by Alan Barr in 1994.Alan H. Barr (1981) ''Superquadrics and Angle-Preserving Transformations''. IEEE Computer Graphics and Applications, volume 1 issue 1. pp. 11-23. Barr's supertoroids have been fairly popular in computer graphics as a convenient model for many objects, such as smooth frames for rectangular things. One quarter of a supertoroid can provide a smooth and seamless 90-degree joint between two superquadric cylinders. However, they are not algebraic surfaces (except in special cases). Formulas Alan Barr's supertoroids are defined by parametric equations similar to the trigonometric equations of the torus, excep ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Implicit Function
In mathematics, an implicit equation is a relation of the form R(x_1, \dots, x_n) = 0, where is a function of several variables (often a polynomial). For example, the implicit equation of the unit circle is x^2 + y^2 - 1 = 0. An implicit function is a function that is defined by an implicit equation, that relates one of the variables, considered as the value of the function, with the others considered as the arguments. For example, the equation x^2 + y^2 - 1 = 0 of the unit circle defines as an implicit function of if , and is restricted to nonnegative values. The implicit function theorem provides conditions under which some kinds of implicit equations define implicit functions, namely those that are obtained by equating to zero multivariable functions that are continuously differentiable. Examples Inverse functions A common type of implicit function is an inverse function. Not all functions have a unique inverse function. If is a function of that has a unique inv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computer Graphics
Computer graphics deals with generating images and art with the aid of computers. Computer graphics is a core technology in digital photography, film, video games, digital art, cell phone and computer displays, and many specialized applications. A great deal of specialized hardware and software has been developed, with the displays of most devices being driven by graphics hardware, computer graphics hardware. It is a vast and recently developed area of computer science. The phrase was coined in 1960 by computer graphics researchers Verne Hudson and William Fetter of Boeing. It is often abbreviated as CG, or typically in the context of film as Computer-generated imagery, computer generated imagery (CGI). The non-artistic aspects of computer graphics are the subject of Computer graphics (computer science), computer science research. Some topics in computer graphics include user interface design, Sprite (computer graphics), sprite graphics, raster graphics, Rendering (computer graph ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Wolfram Demonstrations Project
The Wolfram Demonstrations Project is an open-source collection of interactive programmes called Demonstrations. It is hosted by Wolfram Research. At its launch, it contained 1300 demonstrations but has grown to over 10,000. The site won a Parents' Choice Award in 2008. Wolfram Research's staff organizes and edits the Demonstrations, which may be created by any user of Mathematica, then freely published and freely downloaded. Technology The Demonstrations run in Mathematica 6 or above and in Wolfram CDF Player, which is a free modified version of Wolfram Mathematica and available for Windows, Linux, and macOS and can operate as a web browser plugin. Demonstrations can also be embedded into a website. Each Demonstration page includes a snippet of JavaScript JavaScript (), often abbreviated as JS, is a programming language and core technology of the World Wide Web, alongside HTML and CSS. Ninety-nine percent of websites use JavaScript on the client side for webp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maximum Likelihood Estimation
In statistics, maximum likelihood estimation (MLE) is a method of estimation theory, estimating the Statistical parameter, parameters of an assumed probability distribution, given some observed data. This is achieved by Mathematical optimization, maximizing a likelihood function so that, under the assumed statistical model, the Realization (probability), observed data is most probable. The point estimate, point in the parameter space that maximizes the likelihood function is called the maximum likelihood estimate. The logic of maximum likelihood is both intuitive and flexible, and as such the method has become a dominant means of statistical inference. If the likelihood function is Differentiable function, differentiable, the derivative test for finding maxima can be applied. In some cases, the first-order conditions of the likelihood function can be solved analytically; for instance, the ordinary least squares estimator for a linear regression model maximizes the likelihood when ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Outlier
In statistics, an outlier is a data point that differs significantly from other observations. An outlier may be due to a variability in the measurement, an indication of novel data, or it may be the result of experimental error; the latter are sometimes excluded from the data set. An outlier can be an indication of exciting possibility, but can also cause serious problems in statistical analyses. Outliers can occur by chance in any distribution, but they can indicate novel behaviour or structures in the data-set, measurement error, or that the population has a heavy-tailed distribution. In the case of measurement error, one wishes to discard them or use statistics that are robust statistics, robust to outliers, while in the case of heavy-tailed distributions, they indicate that the distribution has high skewness and that one should be very cautious in using tools or intuitions that assume a normal distribution. A frequent cause of outliers is a mixture of two distributions, wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Group
In mathematics, a Euclidean group is the group of (Euclidean) isometries of a Euclidean space \mathbb^n; that is, the transformations of that space that preserve the Euclidean distance between any two points (also called Euclidean transformations). The group depends only on the dimension ''n'' of the space, and is commonly denoted E(''n'') or ISO(''n''), for ''inhomogeneous special orthogonal'' group. The Euclidean group E(''n'') comprises all translations, rotations, and reflections of \mathbb^n; and arbitrary finite combinations of them. The Euclidean group can be seen as the symmetry group of the space itself, and contains the group of symmetries of any figure (subset) of that space. A Euclidean isometry can be ''direct'' or ''indirect'', depending on whether it preserves the handedness of figures. The direct Euclidean isometries form a subgroup, the special Euclidean group, often denoted SE(''n'') and E+(''n''), whose elements are called rigid motions or Euclidean ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gamma Function
In mathematics, the gamma function (represented by Γ, capital Greek alphabet, Greek letter gamma) is the most common extension of the factorial function to complex numbers. Derived by Daniel Bernoulli, the gamma function \Gamma(z) is defined for all complex numbers z except non-positive integers, and for every positive integer z=n, \Gamma(n) = (n-1)!\,.The gamma function can be defined via a convergent improper integral for complex numbers with positive real part: \Gamma(z) = \int_0^\infty t^ e^\textt, \ \qquad \Re(z) > 0\,.The gamma function then is defined in the complex plane as the analytic continuation of this integral function: it is a meromorphic function which is holomorphic function, holomorphic except at zero and the negative integers, where it has simple Zeros and poles, poles. The gamma function has no zeros, so the reciprocal gamma function is an entire function. In fact, the gamma function corresponds to the Mellin transform of the negative exponential functi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Beta Function
In mathematics, the beta function, also called the Euler integral of the first kind, is a special function that is closely related to the gamma function and to binomial coefficients. It is defined by the integral : \Beta(z_1,z_2) = \int_0^1 t^(1-t)^\,dt for complex number inputs z_1, z_2 such that \operatorname(z_1), \operatorname(z_2)>0. The beta function was studied by Leonhard Euler and Adrien-Marie Legendre and was given its name by Jacques Binet; its symbol is a Greek capital beta. Properties The beta function is symmetric, meaning that \Beta(z_1,z_2) = \Beta(z_2,z_1) for all inputs z_1 and z_2.. Specifically, see 6.2 Beta Function. A key property of the beta function is its close relationship to the gamma function: : \Beta(z_1,z_2)=\frac A proof is given below in . The beta function is also closely related to binomial coefficients. When (or , by symmetry) is a positive integer, it follows from the definition of the gamma function that : \Beta(m,n) =\fr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parametric Representation
In mathematics, a parametric equation expresses several quantities, such as the coordinates of a point, as functions of one or several variables called parameters. In the case of a single parameter, parametric equations are commonly used to express the trajectory of a moving point, in which case, the parameter is often, but not necessarily, time, and the point describes a curve, called a parametric curve. In the case of two parameters, the point describes a surface, called a parametric surface. In all cases, the equations are collectively called a parametric representation, or parametric system, or parameterization (also spelled parametrization, parametrisation) of the object. For example, the equations \begin x &= \cos t \\ y &= \sin t \end form a parametric representation of the unit circle, where is the parameter: A point is on the unit circle if and only if there is a value of such that these two equations generate that point. Sometimes the parametric equations f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
