|
Superellipsoid
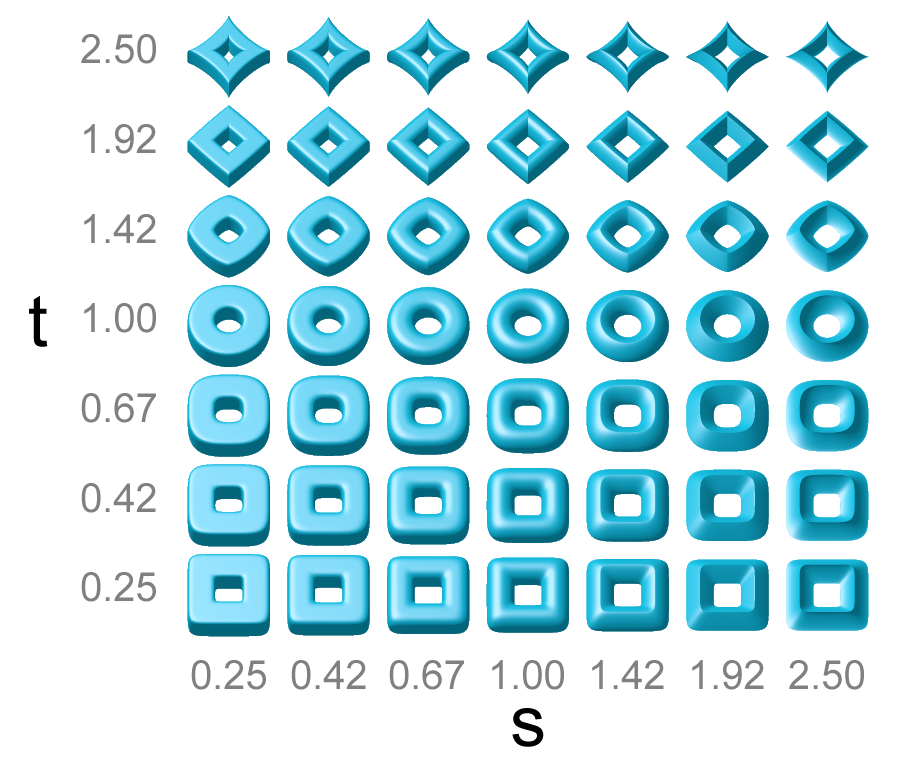
In mathematics, a superellipsoid (or super-ellipsoid) is a solid whose horizontal sections are superellipses (Lamé curves) with the same exponent ''r'', and whose vertical sections through the center are superellipses with the same exponent ''t''. Superellipsoids as computer graphics primitives were popularized by Alan H. Barr (who used the name " superquadrics" to refer to both superellipsoids and supertoroids).Barr, A.H. (January 1981), ''Superquadrics and Angle-Preserving Transformations''. IEEE_CGA vol. 1 no. 1, pp. 11–23Barr, A.H. (1992), ''Rigid Physically Based Superquadrics''. Chapter III.8 of ''Graphics Gems III'', edited by D. Kirk, pp. 137–159 However, while some superellipsoids are superquadrics, neither family is contained in the other. Special cases A handful of notable mathematical figures can arise as special cases of superellipsoids given the correct set of values, which are depicted in the above graphic: * Cylinder * Sphere * Steinmetz solid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Superellipsoid Collection
In mathematics, a superellipsoid (or super-ellipsoid) is a solid whose horizontal sections are superellipses (Lamé curves) with the same exponent ''r'', and whose vertical sections through the center are superellipses with the same exponent ''t''. Superellipsoids as computer graphics primitives were popularized by Alan H. Barr (who used the name "superquadrics" to refer to both superellipsoids and supertoroids).Barr, A.H. (January 1981), ''Superquadrics and Angle-Preserving Transformations''. IEEE_CGA vol. 1 no. 1, pp. 11–23Barr, A.H. (1992), ''Rigid Physically Based Superquadrics''. Chapter III.8 of ''Graphics Gems III'', edited by D. Kirk, pp. 137–159 However, while some superellipsoids are superquadrics, neither family is contained in the other. Special cases A handful of notable mathematical figures can arise as special cases of superellipsoids given the correct set of values, which are depicted in the above graphic: * Cylinder * Sphere * Steinmetz soli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Superellipse
A superellipse, also known as a Lamé curve after Gabriel Lamé, is a closed curve resembling the ellipse, retaining the geometric features of semi-major axis and semi-minor axis, and symmetry about them, but a different overall shape. In the Cartesian coordinate system, the set of all points (x,y) on the curve satisfy the equation :\left, \frac\^n\!\! + \left, \frac\^n\! = 1, where n,a and b are positive numbers, and the vertical bars around a number indicate the absolute value of the number. Specific cases This formula defines a closed curve contained in the rectangle −''a'' ≤ ''x'' ≤ +''a'' and −''b'' ≤ ''y'' ≤ +''b''. The parameters ''a'' and ''b'' are called the ''semi-diameters'' of the curve. The overall shape of the curve is determined by the value of the exponent ''n'', as shown in the following table: If ''n'' 2, a hyperellipse. When ''n'' ≥ 1 and ''a'' = ''b'', the superellipse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Supertoroid
In geometry and computer graphics, a supertoroid or supertorus is usually understood to be a family of doughnut-like surfaces (technically, a topological torus) whose shape is defined by mathematical formulas similar to those that define the superquadrics. The plural of "supertorus" is either supertori or supertoruses. The family was described and named by Alan Barr in 1994.Alan H. Barr (1981) ''Superquadrics and Angle-Preserving Transformations''. IEEE Computer Graphics and Applications, volume 1 issue 1. pp. 11-23. Barr's supertoroids have been fairly popular in computer graphics as a convenient model for many objects, such as smooth frames for rectangular things. One quarter of a supertoroid can provide a smooth and seamless 90-degree joint between two superquadric cylinders. However, they are not algebraic surfaces (except in special cases). Formulas Alan Barr's supertoroids are defined by parametric equations similar to the trigonometric equations of the torus, except ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Piet Hein (Denmark)
Piet Hein (16 December 1905 – 17 April 1996) was a Danish polymath (mathematician, inventor, designer, writer and poet), often writing under the Old Norse pseudonym Kumbel, meaning " tombstone". His short poems, known as '' gruks'' or grooks ( da, gruk), first started to appear in the daily newspaper ''Politiken'' shortly after the German occupation of Denmark in April 1940 under the pseudonym "Kumbel Kumbell". He also invented the Soma cube and the board game Hex. Biography Hein, a direct descendant of Piet Pieterszoon Hein, the 17th century Dutch naval hero, was born in Copenhagen, Denmark. He studied at the Institute for Theoretical Physics (later to become the Niels Bohr Institute) of the University of Copenhagen, and Technical University of Denmark. Yale awarded him an honorary doctorate in 1972. He died in his home on Funen, Denmark in 1996. Resistance Piet Hein, who, in his own words, "played mental ping-pong" with Niels Bohr in the inter-War period, found himself con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gamma Function
In mathematics, the gamma function (represented by , the capital letter gamma from the Greek alphabet) is one commonly used extension of the factorial function to complex numbers. The gamma function is defined for all complex numbers except the non-positive integers. For every positive integer , \Gamma(n) = (n-1)!\,. Derived by Daniel Bernoulli, for complex numbers with a positive real part, the gamma function is defined via a convergent improper integral: \Gamma(z) = \int_0^\infty t^ e^\,dt, \ \qquad \Re(z) > 0\,. The gamma function then is defined as the analytic continuation of this integral function to a meromorphic function that is holomorphic in the whole complex plane except zero and the negative integers, where the function has simple poles. The gamma function has no zeroes, so the reciprocal gamma function is an entire function. In fact, the gamma function corresponds to the Mellin transform of the negative exponential function: \Gamma(z) = \mathcal M ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Beta Function
In mathematics, the beta function, also called the Euler integral of the first kind, is a special function that is closely related to the gamma function and to binomial coefficients. It is defined by the integral : \Beta(z_1,z_2) = \int_0^1 t^(1-t)^\,dt for complex number inputs z_1, z_2 such that \Re(z_1), \Re(z_2)>0. The beta function was studied by Leonhard Euler and Adrien-Marie Legendre and was given its name by Jacques Binet; its symbol is a Greek capital beta. Properties The beta function is symmetric, meaning that \Beta(z_1,z_2) = \Beta(z_2,z_1) for all inputs z_1 and z_2.Davis (1972) 6.2.2 p.258 A key property of the beta function is its close relationship to the gamma function: : \Beta(z_1,z_2)=\frac. A proof is given below in . The beta function is also closely related to binomial coefficients. When (or , by symmetry) is a positive integer, it follows from the definition of the gamma function thatDavis (1972) 6.2.1 p.258 : \Beta(m,n) =\dfrac = \frac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sign Function
In mathematics, the sign function or signum function (from '' signum'', Latin for "sign") is an odd mathematical function that extracts the sign of a real number. In mathematical expressions the sign function is often represented as . To avoid confusion with the sine function, this function is usually called the signum function. Definition The signum function of a real number is a piecewise function which is defined as follows: \sgn x :=\begin -1 & \text x 0. \end Properties Any real number can be expressed as the product of its absolute value and its sign function: x = , x, \sgn x. It follows that whenever is not equal to 0 we have \sgn x = \frac = \frac\,. Similarly, for ''any'' real number , , x, = x\sgn x. We can also ascertain that: \sgn x^n=(\sgn x)^n. The signum function is the derivative of the absolute value function, up to (but not including) the indeterminacy at zero. More formally, in integration theory it is a weak derivative, and in convex fun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parametric Representation
In mathematics, a parametric equation defines a group of quantities as functions of one or more independent variables called parameters. Parametric equations are commonly used to express the coordinates of the points that make up a geometric object such as a curve or surface, in which case the equations are collectively called a parametric representation or parameterization (alternatively spelled as parametrisation) of the object. For example, the equations :\begin x &= \cos t \\ y &= \sin t \end form a parametric representation of the unit circle, where ''t'' is the parameter: A point (''x'', ''y'') is on the unit circle if and only if there is a value of ''t'' such that these two equations generate that point. Sometimes the parametric equations for the individual scalar output variables are combined into a single parametric equation in vectors: :(x, y)=(\cos t, \sin t). Parametric representations are generally nonunique (see the "Examples in two dimensions" section bel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Superegg
In geometry, a superegg is a solid of revolution obtained by rotating an elongated superellipse with exponent greater than 2 around its longest axis. It is a special case of superellipsoid. Unlike an elongated ellipsoid, an elongated superegg can stand upright on a flat surface, or on top of another superegg. This is due to its curvature being zero at the tips. The shape was popularized by Danish poet and scientist Piet Hein (1905–1996). Supereggs of various materials, including brass, were sold as novelties or " executive toys" in the 1960s. Mathematical description The superegg is a superellipsoid whose horizontal cross-sections are circles. It is defined by the inequality :\left, \frac\^p + \left, \frac\^p \leq 1 where ''R'' is the horizontal radius at the "equator" (the widest part), and ''h'' is one half of the height. The exponent ''p'' determines the degree of flattening at the tips and equator. Hein's choice was ''p'' = 2.5 (the same one he used for the Sergel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solid Of Revolution
In geometry, a solid of revolution is a solid figure obtained by rotating a plane figure around some straight line (the '' axis of revolution'') that lies on the same plane. The surface created by this revolution and which bounds the solid is the surface of revolution. Assuming that the curve does not cross the axis, the solid's volume is equal to the length of the circle described by the figure's centroid multiplied by the figure's area ( Pappus's second centroid theorem). A representative disc is a three-dimensional volume element of a solid of revolution. The element is created by rotating a line segment (of length ) around some axis (located units away), so that a cylindrical volume of units is enclosed. Finding the volume Two common methods for finding the volume of a solid of revolution are the disc method and the shell method of integration. To apply these methods, it is easiest to draw the graph in question; identify the area that is to be revolved about the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Meridian Of Longitude
Longitude (, ) is a geographic coordinate that specifies the east–west position of a point on the surface of the Earth, or another celestial body. It is an angular measurement, usually expressed in degrees and denoted by the Greek letter lambda (λ). Meridians are semicircular lines running from pole to pole that connect points with the same longitude. The prime meridian defines 0° longitude; by convention the International Reference Meridian for the Earth passes near the Royal Observatory in Greenwich, England on the island of Great Britain. Positive longitudes are east of the prime meridian, and negative ones are west. Because of the Earth's rotation, there is a close connection between longitude and time measurement. Scientifically precise local time varies with longitude: a difference of 15° longitude corresponds to a one-hour difference in local time, due to the differing position in relation to the Sun. Comparing local time to an absolute measure of time allows l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallel Of Latitude
A circle of latitude or line of latitude on Earth is an abstract east–west small circle connecting all locations around Earth (ignoring elevation) at a given latitude coordinate line. Circles of latitude are often called parallels because they are parallel to each other; that is, planes that contain any of these circles never intersect each other. A location's position along a circle of latitude is given by its longitude. Circles of latitude are unlike circles of longitude, which are all great circles with the centre of Earth in the middle, as the circles of latitude get smaller as the distance from the Equator increases. Their length can be calculated by a common sine or cosine function. The 60th parallel north or south is half as long as the Equator (disregarding Earth's minor flattening by 0.335%). On the Mercator projection or on the Gall-Peters projection, a circle of latitude is perpendicular to all meridians. On the ellipsoid or on spherical projection, all circles ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |