|
Subgame-perfect Equilibrium
In game theory, a subgame perfect equilibrium (or subgame perfect Nash equilibrium) is a refinement of a Nash equilibrium used in dynamic games. A strategy profile is a subgame perfect equilibrium if it represents a Nash equilibrium of every subgame of the original game. Informally, this means that at any point in the game, the players' behavior from that point onward should represent a Nash equilibrium of the continuation game (i.e. of the subgame), no matter what happened before. Every finite extensive game with perfect recall has a subgame perfect equilibrium. Perfect recall is a term introduced by Harold W. Kuhn in 1953 and ''"equivalent to the assertion that each player is allowed by the rules of the game to remember everything he knew at previous moves and all of his choices at those moves"''. A common method for determining subgame perfect equilibria in the case of a finite game is backward induction. Here one first considers the last actions of the game and determi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nash Equilibrium
In game theory, the Nash equilibrium, named after the mathematician John Nash, is the most common way to define the solution of a non-cooperative game involving two or more players. In a Nash equilibrium, each player is assumed to know the equilibrium strategies of the other players, and no one has anything to gain by changing only one's own strategy. The principle of Nash equilibrium dates back to the time of Cournot, who in 1838 applied it to competing firms choosing outputs. If each player has chosen a strategy an action plan based on what has happened so far in the game and no one can increase one's own expected payoff by changing one's strategy while the other players keep their's unchanged, then the current set of strategy choices constitutes a Nash equilibrium. If two players Alice and Bob choose strategies A and B, (A, B) is a Nash equilibrium if Alice has no other strategy available that does better than A at maximizing her payoff in response to Bob choosing B, and Bob ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
One-shot Deviation Principle
The one-shot deviation principle (also known as one-deviation property) is the principle of optimality of dynamic programming applied to game theory. It says that a strategy profile of a finite extensive-form game is a subgame perfect equilibrium (SPE) if and only if there exist no profitable one-shot deviations for each subgame and every player. In simpler terms, if no player can increase their payoffs by deviating a single decision, or period, from their original strategy, then the strategy that they have chosen is a SPE. As a result, no player can profit from deviating from the strategy for one period and then reverting to the strategy. Furthermore, the one-shot deviation principle is very important for infinite horizon games, in which the principle typically does not hold, since it is not plausible to consider an infinite number of strategies and payoffs in order to solve. In an infinite horizon game where the discount factor is less than 1, a strategy profile is a subgame pe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tic-tac-toe
Tic-tac-toe (American English), noughts and crosses (Commonwealth English), or Xs and Os (Canadian or Irish English) is a paper-and-pencil game for two players who take turns marking the spaces in a three-by-three grid with ''X'' or ''O''. The player who succeeds in placing three of their marks in a horizontal, vertical, or diagonal row is the winner. It is a solved game, with a forced draw assuming best play from both players. Gameplay Tic-tac-toe is played on a three-by-three grid by two players, who alternately place the marks X and O in one of the nine spaces in the grid. In the following example, the first player (''X'') wins the game in seven steps: There is no universally-agreed rule as to who plays first, but in this article the convention that X plays first is used. Players soon discover that the best play from both parties leads to a draw. Hence, tic-tac-toe is often played by young children who may not have discovered the optimal strategy. Because of the s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vertex (graph Theory)
In discrete mathematics, and more specifically in graph theory, a vertex (plural vertices) or node is the fundamental unit of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges (unordered pairs of vertices), while a directed graph consists of a set of vertices and a set of arcs (ordered pairs of vertices). In a diagram of a graph, a vertex is usually represented by a circle with a label, and an edge is represented by a line or arrow extending from one vertex to another. From the point of view of graph theory, vertices are treated as featureless and indivisible objects, although they may have additional structure depending on the application from which the graph arises; for instance, a semantic network is a graph in which the vertices represent concepts or classes of objects. The two vertices forming an edge are said to be the endpoints of this edge, and the edge is said to be incident to the vertices. A vertex ''w'' is said to be ad ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Non-credible Threat
A non-credible threat is a term used in game theory and economics to describe a threat in a sequential game that a ''rational'' player would not actually carry out, because it would not be in his best interest to do so. A threat, and its counterparta commitment, are both defined by American economist and Nobel prize winner, T.C. Schelling, who stated that: "A announces that B's behaviour will lead to a response from A. If this response is a reward, then the announcement is a commitment; if this response is a penalty, then the announcement is a threat." While a player might make a threat, it is only deemed credible if it serves the best interest of the player.Heifetz, A., & Yalon-Fortus, J. (2012). Game Theory: Interactive Strategies in Economics and Management. Cambridge University Press. ProQuest Ebook Central In other words, the player would be willing to carry through with the action that is being threatened regardless of the choice of the other player. This is based on the ass ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Extensive Form
An extensive-form game is a specification of a game in game theory, allowing (as the name suggests) for the explicit representation of a number of key aspects, like the sequencing of players' possible moves, their choices at every decision point, the (possibly imperfect) information each player has about the other player's moves when they make a decision, and their payoffs for all possible game outcomes. Extensive-form games also allow for the representation of incomplete information in the form of chance events modeled as " moves by nature". Finite extensive-form games Some authors, particularly in introductory textbooks, initially define the extensive-form game as being just a game tree with payoffs (no imperfect or incomplete information), and add the other elements in subsequent chapters as refinements. Whereas the rest of this article follows this gentle approach with motivating examples, we present upfront the finite extensive-form games as (ultimately) constructed here. This ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complete Information
In economics and game theory, complete information is an economic situation or game in which knowledge about other market participants or players is available to all participants. The utility functions (including risk aversion), payoffs, strategies and "types" of players are thus common knowledge. Complete information is the concept that each player in the game is aware of the sequence, strategies, and payoffs throughout gameplay. Given this information, the players have the ability to plan accordingly based on the information to maximize their own strategies and utility at the end of the game. Inversely, in a game with incomplete information, players do not possess full information about their opponents. Some players possess private information, a fact that the others should take into account when forming expectations about how those players will behave. A typical example is an auction: each player knows his own utility function (valuation for the item), but does not know the utili ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mixed Strategy
In game theory, a player's strategy is any of the options which they choose in a setting where the outcome depends ''not only'' on their own actions ''but'' on the actions of others. The discipline mainly concerns the action of a player in a game affecting the behavior or actions of other players. Some examples of "games" include chess, bridge, poker, monopoly, diplomacy or battleship. A player's strategy will determine the action which the player will take at any stage of the game. In studying game theory, economists enlist a more rational lens in analyzing decisions rather than the psychological or sociological perspectives taken when analyzing relationships between decisions of two or more parties in different disciplines. The strategy concept is sometimes (wrongly) confused with that of a move. A move is an action taken by a player at some point during the play of a game (e.g., in chess, moving white's Bishop a2 to b3). A strategy on the other hand is a complete algorithm for p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tic Tac Toe
Tic-tac-toe (American English), noughts and crosses (Commonwealth English), or Xs and Os (Canadian or Irish English) is a paper-and-pencil game for two players who take turns marking the spaces in a three-by-three grid with ''X'' or ''O''. The player who succeeds in placing three of their marks in a horizontal, vertical, or diagonal row is the winner. It is a solved game, with a forced draw assuming best play from both players. Gameplay Tic-tac-toe is played on a three-by-three grid by two players, who alternately place the marks X and O in one of the nine spaces in the grid. In the following example, the first player (''X'') wins the game in seven steps: There is no universally-agreed rule as to who plays first, but in this article the convention that X plays first is used. Players soon discover that the best play from both parties leads to a draw. Hence, tic-tac-toe is often played by young children who may not have discovered the optimal strategy. Because of the s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prisoner's Dilemma
The Prisoner's Dilemma is an example of a game analyzed in game theory. It is also a thought experiment that challenges two completely rational agents to a dilemma: cooperate with their partner for mutual reward, or betray their partner ("defect") for individual reward. This dilemma was originally framed by Merrill Flood and Melvin Dresher while working at RAND in 1950. Albert W. Tucker appropriated the game and formalized it by structuring the rewards in terms of prison sentences and named it "prisoner's dilemma". William Poundstone in his 1993 book ''Prisoner's Dilemma'' writes the following version:Two members of a criminal gang are arrested and imprisoned. Each prisoner is in solitary confinement with no means of speaking to or exchanging messages with the other. The police admit they don't have enough evidence to convict the pair on the principal charge. They plan to sentence both to two years in prison on a lesser charge. Simultaneously, the police offer each prisoner a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
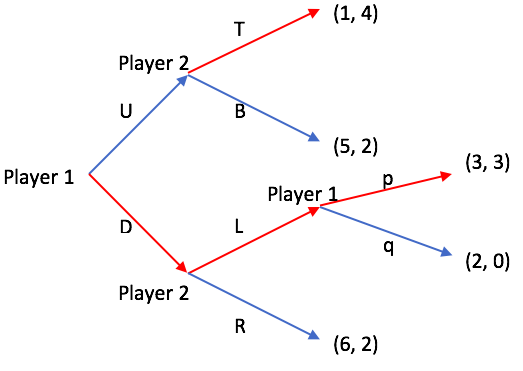
Subgame 1 Solved
In game theory, a subgame is any part (a subset) of a game that meets the following criteria (the following terms allude to a game described in extensive form): #It has a single initial node that is the only member of that node's information set (i.e. the initial node is in a singleton information set). #If a node is contained in the subgame then so are all of its successors. #If a node in a particular information set is in the subgame then all members of that information set belong to the subgame. It is a notion used in the solution concept of subgame perfect Nash equilibrium, a refinement of the Nash equilibrium that eliminates non-credible threats. The key feature of a subgame is that it, when seen in isolation, constitutes a game in its own right. When the initial node of a subgame is reached in a larger game, players can concentrate only on that subgame; they can ignore the history of the rest of the game (provided they know what subgame they are playing). This is the i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |