|
One-shot Deviation Principle
The one-shot deviation principle (also known as one-deviation property) is the principle of optimality of dynamic programming applied to game theory. It says that a strategy profile of a finite extensive-form game is a subgame perfect equilibrium (SPE) if and only if there exist no profitable one-shot deviations for each subgame and every player. In simpler terms, if no player can increase their payoffs by deviating a single decision, or period, from their original strategy, then the strategy that they have chosen is a SPE. As a result, no player can profit from deviating from the strategy for one period and then reverting to the strategy. Furthermore, the one-shot deviation principle is very important for infinite horizon games, in which the principle typically does not hold, since it is not plausible to consider an infinite number of strategies and payoffs in order to solve. In an infinite horizon game where the discount factor is less than 1, a strategy profile is a subgame pe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamic Programming
Dynamic programming is both a mathematical optimization method and a computer programming method. The method was developed by Richard Bellman in the 1950s and has found applications in numerous fields, from aerospace engineering to economics. In both contexts it refers to simplifying a complicated problem by breaking it down into simpler sub-problems in a recursive manner. While some decision problems cannot be taken apart this way, decisions that span several points in time do often break apart recursively. Likewise, in computer science, if a problem can be solved optimally by breaking it into sub-problems and then recursively finding the optimal solutions to the sub-problems, then it is said to have ''optimal substructure''. If sub-problems can be nested recursively inside larger problems, so that dynamic programming methods are applicable, then there is a relation between the value of the larger problem and the values of the sub-problems.Cormen, T. H.; Leiserson, C. E.; Rives ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Game Theory
Game theory is the study of mathematical models of strategic interactions among rational agents. Myerson, Roger B. (1991). ''Game Theory: Analysis of Conflict,'' Harvard University Press, p.&nbs1 Chapter-preview links, ppvii–xi It has applications in all fields of social science, as well as in logic, systems science and computer science. Originally, it addressed two-person zero-sum games, in which each participant's gains or losses are exactly balanced by those of other participants. In the 21st century, game theory applies to a wide range of behavioral relations; it is now an umbrella term for the science of logical decision making in humans, animals, as well as computers. Modern game theory began with the idea of mixed-strategy equilibria in two-person zero-sum game and its proof by John von Neumann. Von Neumann's original proof used the Brouwer fixed-point theorem on continuous mappings into compact convex sets, which became a standard method in game theory and mathema ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Extensive-form Game
An extensive-form game is a specification of a game in game theory, allowing (as the name suggests) for the explicit representation of a number of key aspects, like the sequencing of players' possible moves, their choices at every decision point, the (possibly imperfect) information each player has about the other player's moves when they make a decision, and their payoffs for all possible game outcomes. Extensive-form games also allow for the representation of incomplete information in the form of chance events modeled as " moves by nature". Finite extensive-form games Some authors, particularly in introductory textbooks, initially define the extensive-form game as being just a game tree with payoffs (no imperfect or incomplete information), and add the other elements in subsequent chapters as refinements. Whereas the rest of this article follows this gentle approach with motivating examples, we present upfront the finite extensive-form games as (ultimately) constructed here. This ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subgame Perfect Equilibrium
In game theory, a subgame perfect equilibrium (or subgame perfect Nash equilibrium) is a refinement of a Nash equilibrium used in dynamic games. A strategy profile is a subgame perfect equilibrium if it represents a Nash equilibrium of every subgame of the original game. Informally, this means that at any point in the game, the players' behavior from that point onward should represent a Nash equilibrium of the continuation game (i.e. of the subgame), no matter what happened before. Every finite extensive game with perfect recall has a subgame perfect equilibrium. Perfect recall is a term introduced by Harold W. Kuhn in 1953 and ''"equivalent to the assertion that each player is allowed by the rules of the game to remember everything he knew at previous moves and all of his choices at those moves"''. A common method for determining subgame perfect equilibria in the case of a finite game is backward induction. Here one first considers the last actions of the game and determ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
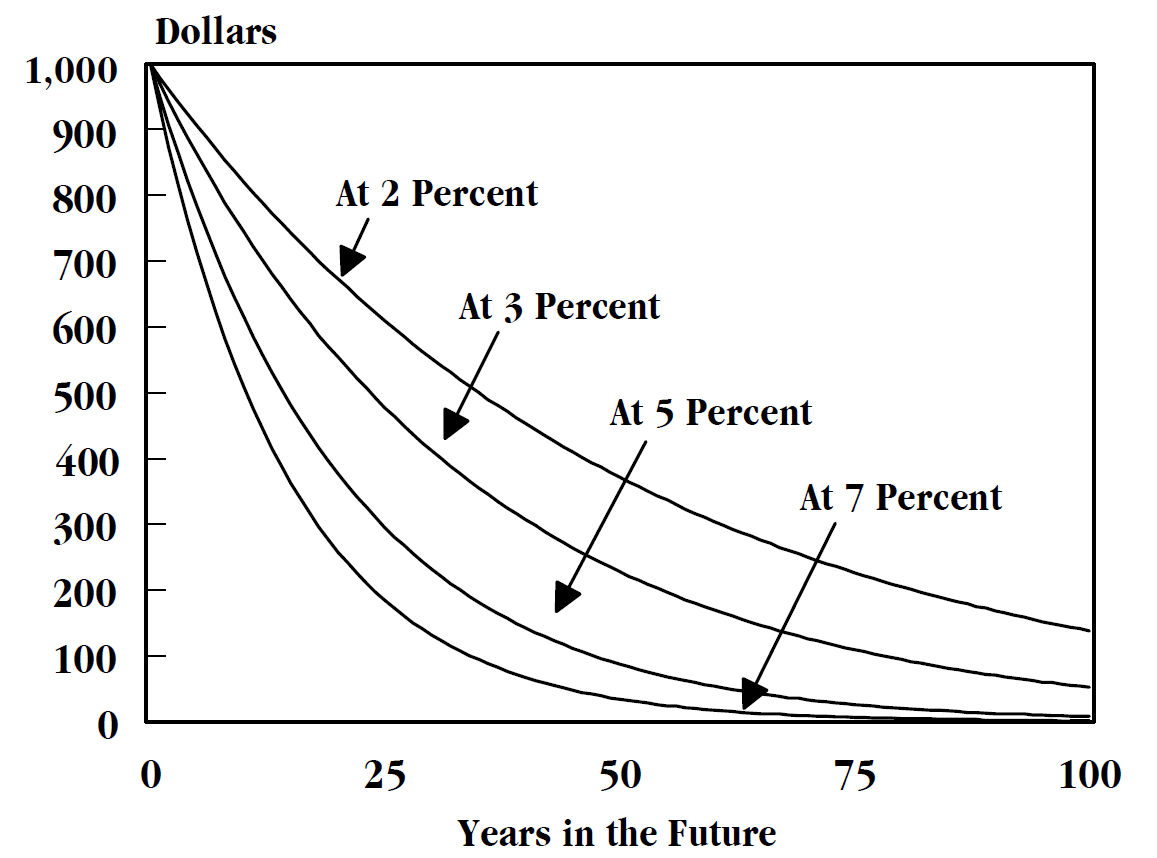
Discount Factor
Discounting is a financial mechanism in which a debtor obtains the right to delay payments to a creditor, for a defined period of time, in exchange for a charge or fee.See "Time Value", "Discount", "Discount Yield", "Compound Interest", "Efficient Market", "Market Value" and "Opportunity Cost" in Downes, J. and Goodman, J. E. ''Dictionary of Finance and Investment Terms'', Baron's Financial Guides, 2003. Essentially, the party that owes money in the present purchases the right to delay the payment until some future date.See "Discount", "Compound Interest", "Efficient Markets Hypothesis", "Efficient Resource Allocation", "Pareto-Optimality", "Price", "Price Mechanism" and "Efficient Market" in Black, John, ''Oxford Dictionary of Economics'', Oxford University Press, 2002. This transaction is based on the fact that most people prefer current interest to delayed interest because of mortality effects, impatience effects, and salience effects. The discount, or charge, is the difference ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetric Game
In game theory, a symmetric game is a game where the payoffs for playing a particular strategy depend only on the other strategies employed, not on who is playing them. If one can change the identities of the players without changing the payoff to the strategies, then a game is symmetric. Symmetry can come in different varieties. Ordinally symmetric games are games that are symmetric with respect to the ordinal structure of the payoffs. A game is quantitatively symmetric if and only if it is symmetric with respect to the exact payoffs. A partnership game is a symmetric game where both players receive identical payoffs for any strategy set. That is, the payoff for playing strategy ''a'' against strategy ''b'' receives the same payoff as playing strategy ''b'' against strategy ''a''. Symmetry in 2x2 games Only 12 out of the 144 ordinally distinct 2x2 games are symmetric. However, many of the commonly studied 2x2 games are at least ordinally symmetric. The standard represent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |