|
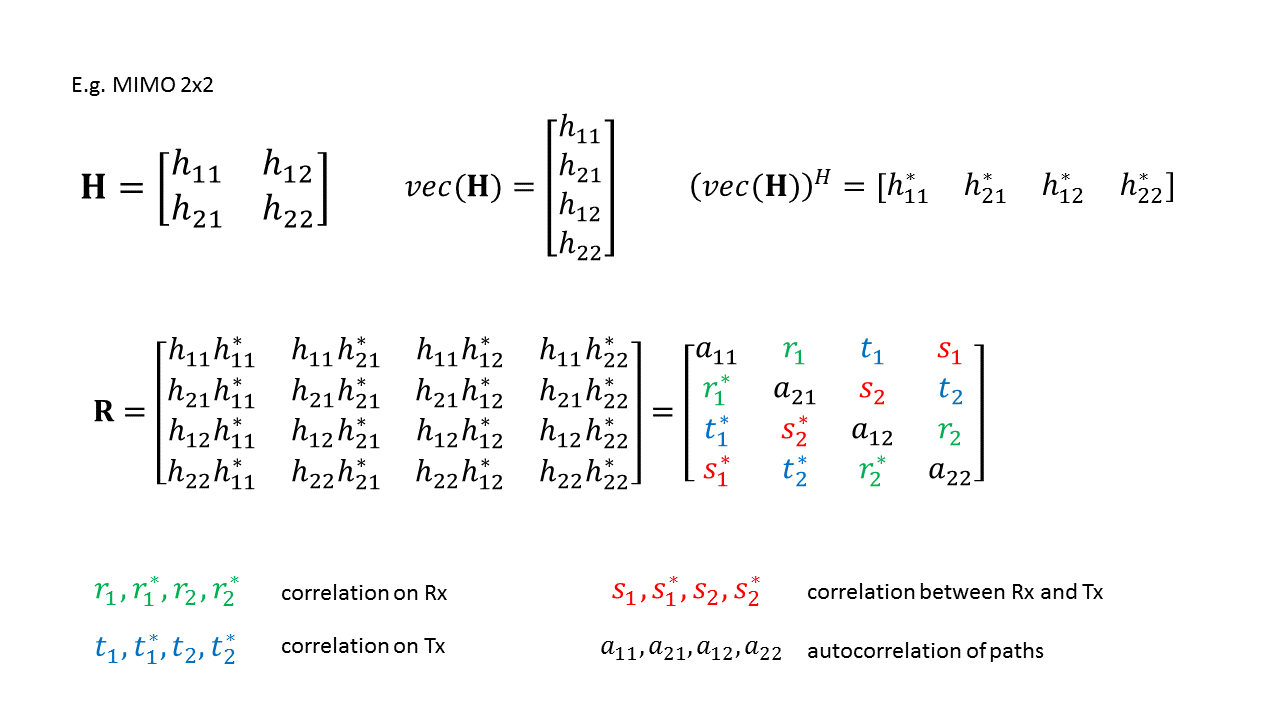
Spatial Correlation
In wireless communication, spatial correlation is the correlation between a signal's spatial direction and the average received signal gain. Theoretically, the performance of wireless communication systems can be improved by having multiple antennas at the transmitter and the receiver. The idea is that if the propagation channels between each pair of transmit and receive antennas are statistically independent and identically distributed, then multiple independent channels with identical characteristics can be created by precoding and be used for either transmitting multiple data streams or increasing the reliability (in terms of bit error rate). In practice, the channels between different antennas are often correlated and therefore the potential multi antenna gains may not always be obtainable. Existence In an ideal communication scenario, there is a line-of-sight path between the transmitter and receiver that represents clear spatial channel characteristics. In urban cellul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wireless Communication
Wireless communication (or just wireless, when the context allows) is the transfer of information between two or more points without the use of an electrical conductor, optical fiber or other continuous guided medium for the transfer. The most common wireless technologies use radio waves. With radio waves, intended distances can be short, such as a few meters for Bluetooth or as far as millions of kilometers for deep-space radio communications. It encompasses various types of fixed, mobile, and portable applications, including two-way radios, cellular telephones, personal digital assistants (PDAs), and wireless networking. Other examples of applications of radio ''wireless technology'' include GPS units, garage door openers, wireless computer mouse, keyboards and headsets, headphones, radio receivers, satellite television, broadcast television and cordless telephones. Somewhat less common methods of achieving wireless communications involve other electromagnetic phenomena, such ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Narrowband
Narrowband signals are signals that occupy a narrow range of frequencies or that have a small fractional bandwidth. In the audio spectrum, narrowband sounds are sounds that occupy a narrow range of frequencies. In telephony, narrowband is usually considered to cover frequencies 300–3400 Hz, i.e. the voiceband. In radio communications, a narrowband channel is a channel in which the bandwidth of the message does not significantly exceed the channel's coherence bandwidth. In the study of wired channels, ''narrowband'' implies that the channel under consideration is sufficiently narrow that its frequency response can be considered flat. The message bandwidth will therefore be less than the coherence bandwidth of the channel. That is, no channel has perfectly flat fading, but the analysis of many aspects of wireless systems is greatly simplified if flat fading can be assumed. Two-way radio narrowband Two-Way Radio Narrowbanding refers to a U.S. Federal Communications Commiss ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bit Error Rate
In digital transmission, the number of bit errors is the number of received bits of a data stream over a communication channel that have been altered due to noise, interference, distortion or bit synchronization errors. The bit error rate (BER) is the number of bit errors per unit time. The bit error ratio (also BER) is the number of bit errors divided by the total number of transferred bits during a studied time interval. Bit error ratio is a unitless performance measure, often expressed as a percentage. The bit error probability ''pe'' is the expected value of the bit error ratio. The bit error ratio can be considered as an approximate estimate of the bit error probability. This estimate is accurate for a long time interval and a high number of bit errors. Example As an example, assume this transmitted bit sequence: 1 1 0 0 0 1 0 1 1 and the following received bit sequence: 0 1 0 1 0 1 0 0 1, The number of bit errors (the underlined bits) is, in this case, 3. The BER is 3 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Information Theory
Information theory is the scientific study of the quantification (science), quantification, computer data storage, storage, and telecommunication, communication of information. The field was originally established by the works of Harry Nyquist and Ralph Hartley, in the 1920s, and Claude Shannon in the 1940s. The field is at the intersection of probability theory, statistics, computer science, statistical mechanics, information engineering (field), information engineering, and electrical engineering. A key measure in information theory is information entropy, entropy. Entropy quantifies the amount of uncertainty involved in the value of a random variable or the outcome of a random process. For example, identifying the outcome of a fair coin flip (with two equally likely outcomes) provides less information (lower entropy) than specifying the outcome from a roll of a dice, die (with six equally likely outcomes). Some other important measures in information theory are mutual informat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Majorization
In mathematics, majorization is a preorder on vectors of real numbers. Let ^_,\ i=1,\,\ldots,\,n denote the i-th largest element of the vector \mathbf\in\mathbb^n. Given \mathbf,\ \mathbf \in \mathbb^n, we say that \mathbf weakly majorizes (or dominates) \mathbf from below (or equivalently, we say that \mathbf is weakly majorized (or dominated) by \mathbf from below) denoted as \mathbf \succ_w \mathbf if \sum_^k x_^ \geq \sum_^k y_^ for all k=1,\,\dots,\,d. If in addition \sum_^d x_i^ = \sum_^d y_i^, we say that \mathbf majorizes (or dominates) \mathbf , written as \mathbf \succ \mathbf , or equivalently, we say that \mathbf is majorized (or dominated) by \mathbf. The order of the entries of the vectors \mathbf or \mathbf does not affect the majorization, e.g., the statement (1,2)\prec (0,3) is simply equivalent to (2,1)\prec (3,0). As a consequence, majorization is not a partial order, since \mathbf \succ \mathbf and \mathbf \succ \mathbf do not imply \mathbf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenvalue, Eigenvector And Eigenspace
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted by \lambda, is the factor by which the eigenvector is scaled. Geometrically, an eigenvector, corresponding to a real nonzero eigenvalue, points in a direction in which it is stretched by the transformation and the eigenvalue is the factor by which it is stretched. If the eigenvalue is negative, the direction is reversed. Loosely speaking, in a multidimensional vector space, the eigenvector is not rotated. Formal definition If is a linear transformation from a vector space over a field into itself and is a nonzero vector in , then is an eigenvector of if is a scalar multiple of . This can be written as T(\mathbf) = \lambda \mathbf, where is a scalar in , known as the eigenvalue, characteristic value, or characteristic root as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kronecker Product
In mathematics, the Kronecker product, sometimes denoted by ⊗, is an operation on two matrices of arbitrary size resulting in a block matrix. It is a generalization of the outer product (which is denoted by the same symbol) from vectors to matrices, and gives the matrix of the tensor product linear map with respect to a standard choice of basis. The Kronecker product is to be distinguished from the usual matrix multiplication, which is an entirely different operation. The Kronecker product is also sometimes called matrix direct product. The Kronecker product is named after the German mathematician Leopold Kronecker (1823–1891), even though there is little evidence that he was the first to define and use it. The Kronecker product has also been called the ''Zehfuss matrix'', and the ''Zehfuss product'', after , who in 1858 described this matrix operation, but Kronecker product is currently the most widely used. Definition If A is an matrix and B is a matrix, then the Kr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Normal Distribution
In probability theory, the family of complex normal distributions, denoted \mathcal or \mathcal_, characterizes complex random variables whose real and imaginary parts are jointly normal. The complex normal family has three parameters: ''location'' parameter ''μ'', ''covariance'' matrix \Gamma, and the ''relation'' matrix C. The standard complex normal is the univariate distribution with \mu = 0, \Gamma=1, and C=0. An important subclass of complex normal family is called the circularly-symmetric (central) complex normal and corresponds to the case of zero relation matrix and zero mean: \mu = 0 and C=0 . This case is used extensively in signal processing, where it is sometimes referred to as just complex normal in the literature. Definitions Complex standard normal random variable The standard complex normal random variable or standard complex Gaussian random variable is a complex random variable Z whose real and imaginary parts are independent normally distributed random var ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rayleigh Fading
Rayleigh fading is a statistical model for the effect of a propagation environment on a radio signal, such as that used by wireless devices. Rayleigh fading models assume that the magnitude of a signal that has passed through such a transmission medium (also called a communication channel) will vary randomly, or fade, according to a Rayleigh distribution — the radial component of the sum of two uncorrelated Gaussian random variables. Rayleigh fading is viewed as a reasonable model for tropospheric and ionospheric signal propagation as well as the effect of heavily built-up urban environments on radio signals. Rayleigh fading is most applicable when there is no dominant propagation along a line of sight between the transmitter and receiver. If there is a dominant line of sight, Rician fading may be more applicable. Rayleigh fading is a special case of two-wave with diffuse power (TWDP) fading. The model Rayleigh fading is a reasonable model when there are many objects in the en ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conjugate Transpose
In mathematics, the conjugate transpose, also known as the Hermitian transpose, of an m \times n complex matrix \boldsymbol is an n \times m matrix obtained by transposing \boldsymbol and applying complex conjugate on each entry (the complex conjugate of a+ib being a-ib, for real numbers a and b). It is often denoted as \boldsymbol^\mathrm or \boldsymbol^* or \boldsymbol'. H. W. Turnbull, A. C. Aitken, "An Introduction to the Theory of Canonical Matrices," 1932. For real matrices, the conjugate transpose is just the transpose, \boldsymbol^\mathrm = \boldsymbol^\mathsf. Definition The conjugate transpose of an m \times n matrix \boldsymbol is formally defined by where the subscript ij denotes the (i,j)-th entry, for 1 \le i \le n and 1 \le j \le m, and the overbar denotes a scalar complex conjugate. This definition can also be written as :\boldsymbol^\mathrm = \left(\overline\right)^\mathsf = \overline where \boldsymbol^\mathsf denotes the transpose and \overline denotes the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expected Value
In probability theory, the expected value (also called expectation, expectancy, mathematical expectation, mean, average, or first moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean of a large number of independently selected outcomes of a random variable. The expected value of a random variable with a finite number of outcomes is a weighted average of all possible outcomes. In the case of a continuum of possible outcomes, the expectation is defined by integration. In the axiomatic foundation for probability provided by measure theory, the expectation is given by Lebesgue integration. The expected value of a random variable is often denoted by , , or , with also often stylized as or \mathbb. History The idea of the expected value originated in the middle of the 17th century from the study of the so-called problem of points, which seeks to divide the stakes ''in a fair way'' between two players, who have to end th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |