Sparse Approximation

	Sparse Approximation Sparse approximation (also known as sparse representation) theory deals with sparse solutions for systems of linear equations. Techniques for finding these solutions and exploiting them in applications have found wide use in image processing, signal processing, machine learning, medical imaging, and more. Sparse decomposition Noiseless observations Consider a linear system of equations x = D\alpha, where D is an underdetermined m\times p matrix (m < p) and $x \in \mathbb^m,\alpha \in \mathbb^p$ . The matrix $D$ (typically assumed to be full-rank) is referred to as the dictionary, and $x$ is a signal of interest. The core sparse representation problem is defined as the quest for the sparsest possible representation $\alpha$ satisfying $x = D\alpha$ . Due to the underdetermined nature of $D$ , this linear system admits in general infinitely many possible solutions, and among these we seek the one with the fewe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon]
	Sparsity In numerical analysis and scientific computing, a sparse matrix or sparse array is a matrix in which most of the elements are zero. There is no strict definition regarding the proportion of zero-value elements for a matrix to qualify as sparse but a common criterion is that the number of non-zero elements is roughly equal to the number of rows or columns. By contrast, if most of the elements are non-zero, the matrix is considered dense. The number of zero-valued elements divided by the total number of elements (e.g., ''m'' × ''n'' for an ''m'' × ''n'' matrix) is sometimes referred to as the sparsity of the matrix. Conceptually, sparsity corresponds to systems with few pairwise interactions. For example, consider a line of balls connected by springs from one to the next: this is a sparse system, as only adjacent balls are coupled. By contrast, if the same line of balls were to have springs connecting each ball to all other balls, the system would correspond to a dense matrix. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon]
	Restricted Isometry Property In linear algebra, the restricted isometry property (RIP) characterizes matrices which are nearly orthonormal, at least when operating on sparse vectors. The concept was introduced by Emmanuel Candès and Terence TaoE. J. Candes and T. Tao, "Decoding by Linear Programming," IEEE Trans. Inf. Th., 51(12): 4203–4215 (2005). and is used to prove many theorems in the field of compressed sensing. There are no known large matrices with bounded restricted isometry constants (computing these constants is strongly NP-hard, and is hard to approximate as well), but many random matrices have been shown to remain bounded. In particular, it has been shown that with exponentially high probability, random Gaussian, Bernoulli, and partial Fourier matrices satisfy the RIP with number of measurements nearly linear in the sparsity level. The current smallest upper bounds for any large rectangular matrices are for those of Gaussian matrices. Web forms to evaluate bounds for the Gaussian ensemble ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon]
picture info	Regularization (mathematics) In mathematics, statistics, Mathematical finance, finance, and computer science, particularly in machine learning and inverse problems, regularization is a process that converts the Problem solving, answer to a problem to a simpler one. It is often used in solving ill-posed problems or to prevent overfitting. Although regularization procedures can be divided in many ways, the following delineation is particularly helpful: * Explicit regularization is regularization whenever one explicitly adds a term to the optimization problem. These terms could be Prior probability, priors, penalties, or constraints. Explicit regularization is commonly employed with ill-posed optimization problems. The regularization term, or penalty, imposes a cost on the optimization function to make the optimal solution unique. * Implicit regularization is all other forms of regularization. This includes, for example, early stopping, using a robust loss function, and discarding outliers. Implicit regularizat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon]
picture info	Data Mining Data mining is the process of extracting and finding patterns in massive data sets involving methods at the intersection of machine learning, statistics, and database systems. Data mining is an interdisciplinary subfield of computer science and statistics with an overall goal of extracting information (with intelligent methods) from a data set and transforming the information into a comprehensible structure for further use. Data mining is the analysis step of the " knowledge discovery in databases" process, or KDD. Aside from the raw analysis step, it also involves database and data management aspects, data pre-processing, model and inference considerations, interestingness metrics, complexity considerations, post-processing of discovered structures, visualization, and online updating. The term "data mining" is a misnomer because the goal is the extraction of patterns and knowledge from large amounts of data, not the extraction (''mining'') of data itself. It also is a buzzwo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon]
picture info	Array Processing Array processing is a wide area of research in the field of signal processing that extends from the simplest form of 1 dimensional line arrays to 2 and 3 dimensional array geometries. Array structure can be defined as a set of sensors that are spatially separated, e.g. radio antenna and seismic arrays. The sensors used for a specific problem may vary widely, for example microphones, accelerometers and telescopes. However, many similarities exist, the most fundamental of which may be an assumption of wave propagation. Wave propagation means there is a systemic relationship between the signal received on spatially separated sensors. By creating a physical model of the wave propagation, or in machine learning applications a training data set, the relationships between the signals received on spatially separated sensors can be leveraged for many applications. Some common problem that are solved with array processing techniques are: * determine number and locations of energy-radiatin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon]
	Proximal Gradient Method Proximal gradient methods are a generalized form of projection used to solve non-differentiable convex optimization problems. Many interesting problems can be formulated as convex optimization problems of the form \operatorname\limits_ \sum_^n f_i(x) where f_i: \mathbb^N \rightarrow \mathbb,\ i = 1, \dots, n are possibly non-differentiable convex functions. The lack of differentiability rules out conventional smooth optimization techniques like the steepest descent method and the conjugate gradient method, but proximal gradient methods can be used instead. Proximal gradient methods starts by a splitting step, in which the functions f_1, . . . , f_n are used individually so as to yield an easily implementable algorithm. They are called proximal because each non-differentiable function among f_1, . . . , f_n is involved via its proximity operator. Iterative shrinkage thresholding algorithm, projected Landweber, projected gradient, alternating projections, alternating ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon]
picture info	Coordinate Descent Coordinate descent is an optimization algorithm that successively minimizes along coordinate directions to find the minimum of a function. At each iteration, the algorithm determines a coordinate or coordinate block via a coordinate selection rule, then exactly or inexactly minimizes over the corresponding coordinate hyperplane while fixing all other coordinates or coordinate blocks. A line search along the coordinate direction can be performed at the current iterate to determine the appropriate step size. Coordinate descent is applicable in both differentiable and derivative-free contexts. Description Coordinate descent is based on the idea that the minimization of a multivariable function F(\mathbf) can be achieved by minimizing it along one direction at a time, i.e., solving univariate (or at least much simpler) optimization problems in a loop. In the simplest case of ''cyclic coordinate descent'', one cyclically iterates through the directions, one at a time, minimizing the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon]
	Least-angle Regression In statistics, least-angle regression (LARS) is an algorithm for fitting linear regression models to high-dimensional data, developed by Bradley Efron, Trevor Hastie, Iain Johnstone and Robert Tibshirani. Suppose we expect a response variable to be determined by a linear combination of a subset of potential covariates. Then the LARS algorithm provides a means of producing an estimate of which variables to include, as well as their coefficients. Instead of giving a vector result, the LARS solution consists of a curve denoting the solution for each value of the L1 norm of the parameter vector. The algorithm is similar to forward stepwise regression, but instead of including variables at each step, the estimated parameters are increased in a direction equiangular to each one's correlations with the residual. Pros and cons The advantages of the LARS method are: # It is computationally just as fast as forward selection. # It produces a full piecewise linear solution path, whic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon]
	Iteratively Reweighted Least Squares The method of iteratively reweighted least squares (IRLS) is used to solve certain optimization problems with objective functions of the form of a ''p''-norm: \mathop_ \sum_^n \big, y_i - f_i (\boldsymbol\beta) \big, ^p, by an iterative method in which each step involves solving a weighted least squares problem of the form:C. Sidney Burrus, Iterative Reweighted Least Squares' \boldsymbol\beta^ = \underset \sum_^n w_i (\boldsymbol\beta^) \big, y_i - f_i (\boldsymbol\beta) \big, ^2. IRLS is used to find the maximum likelihood estimates of a generalized linear model, and in robust regression to find an M-estimator, as a way of mitigating the influence of outliers in an otherwise normally-distributed data set, for example, by minimizing the least absolute errors rather than the least square errors. One of the advantages of IRLS over linear programming and convex programming is that it can be used with Gauss–Newton and Levenberg–Marquardt numerical algorithms. Exam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon]
	Basis Pursuit Denoising In applied mathematics and statistics, basis pursuit denoising (BPDN) refers to a mathematical optimization problem of the form : \min_x \left(\frac \, y - Ax\, ^2_2 + \lambda \, x\, _1\right), where \lambda is a parameter that controls the trade-off between sparsity and reconstruction fidelity, x is an N \times 1 solution vector, y is an M \times 1 vector of observations, A is an M \times N transform matrix and M < N. This is an instance of convex optimization . Some authors refer to basis pursuit denoising as the following closely related problem: : $\min_x \, x\, _1 \text \, y - Ax\, ^2_2 \le \delta,$ which, for any given $\lambda$ , is equivalent to the unconstrained formulation for some (usually unknown ''a priori'') value of $\delta$ . The two problems are quite similar. In practice, the unconstrained fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon]
picture info	Least Squares The method of least squares is a mathematical optimization technique that aims to determine the best fit function by minimizing the sum of the squares of the differences between the observed values and the predicted values of the model. The method is widely used in areas such as regression analysis, curve fitting and data modeling. The least squares method can be categorized into linear and nonlinear forms, depending on the relationship between the model parameters and the observed data. The method was first proposed by Adrien-Marie Legendre in 1805 and further developed by Carl Friedrich Gauss. History Founding The method of least squares grew out of the fields of astronomy and geodesy, as scientists and mathematicians sought to provide solutions to the challenges of navigating the Earth's oceans during the Age of Discovery. The accurate description of the behavior of celestial bodies was the key to enabling ships to sail in open seas, where sailors could no longer rely on la ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon]
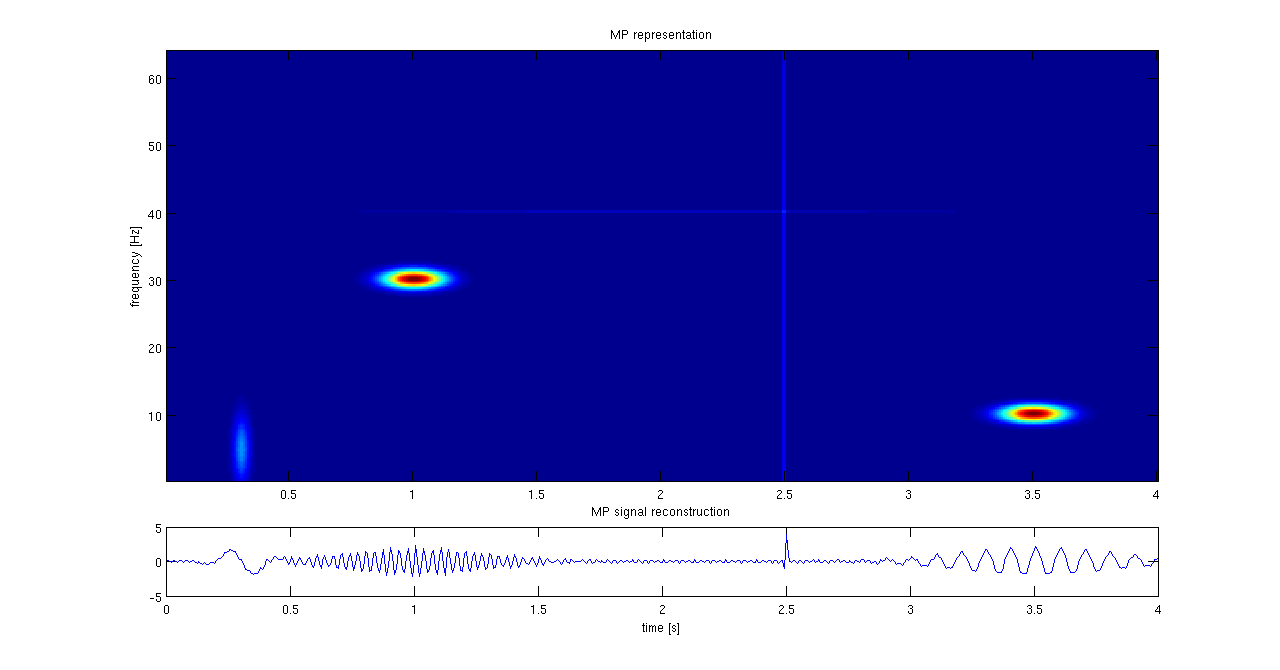
picture info	Matching Pursuit Matching pursuit (MP) is a sparse approximation algorithm which finds the "best matching" projections of multidimensional data onto the span of an over-complete (i.e., redundant) dictionary D. The basic idea is to approximately represent a signal f from Hilbert space H as a weighted sum of finitely many functions g_ (called atoms) taken from D. An approximation with N atoms has the form : f(t) \approx \hat f_N(t) := \sum_^ a_n g_(t) where g_ is the \gamma_nth column of the matrix D and a_n is the scalar weighting factor (amplitude) for the atom g_. Normally, not every atom in D will be used in this sum. Instead, matching pursuit chooses the atoms one at a time in order to maximally (greedily) reduce the approximation error. This is achieved by finding the atom that has the highest inner product with the signal (assuming the atoms are normalized), subtracting from the signal an approximation that uses only that one atom, and repeating the process until the signal is satisfactoril ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon]