|
Spacetime Topology
Spacetime topology is the topological structure of spacetime, a topic studied primarily in general relativity. This physical theory models gravitation as the curvature of a four dimensional Lorentzian manifold (a spacetime) and the concepts of topology thus become important in analysing local as well as global aspects of spacetime. The study of spacetime topology is especially important in physical cosmology. Types of topology There are two main types of topology for a spacetime ''M''. Manifold topology As with any manifold, a spacetime possesses a natural manifold topology. Here the open sets are the image of open sets in \mathbb^4. Path or Zeeman topology ''Definition'':Luca Bombelli website The topology in which a subset is |
Topological Space
In mathematics, a topological space is, roughly speaking, a geometrical space in which closeness is defined but cannot necessarily be measured by a numeric distance. More specifically, a topological space is a set whose elements are called points, along with an additional structure called a topology, which can be defined as a set of neighbourhoods for each point that satisfy some axioms formalizing the concept of closeness. There are several equivalent definitions of a topology, the most commonly used of which is the definition through open sets, which is easier than the others to manipulate. A topological space is the most general type of a mathematical space that allows for the definition of limits, continuity, and connectedness. Common types of topological spaces include Euclidean spaces, metric spaces and manifolds. Although very general, the concept of topological spaces is fundamental, and used in virtually every branch of modern mathematics. The study of topological spac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Locally Compact Space
In topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space. More precisely, it is a topological space in which every point has a compact neighborhood. In mathematical analysis locally compact spaces that are Hausdorff are of particular interest; they are abbreviated as LCH spaces. Formal definition Let ''X'' be a topological space. Most commonly ''X'' is called locally compact if every point ''x'' of ''X'' has a compact neighbourhood, i.e., there exists an open set ''U'' and a compact set ''K'', such that x\in U\subseteq K. There are other common definitions: They are all equivalent if ''X'' is a Hausdorff space (or preregular). But they are not equivalent in general: :1. every point of ''X'' has a compact neighbourhood. :2. every point of ''X'' has a closed compact neighbourhood. :2′. every point of ''X'' has a relatively compact neighbourho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
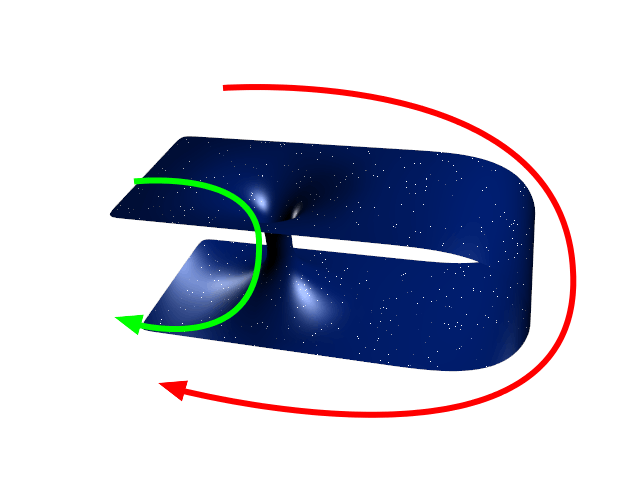
Wormhole
A wormhole (Einstein-Rosen bridge) is a hypothetical structure connecting disparate points in spacetime, and is based on a special Solutions of the Einstein field equations, solution of the Einstein field equations. A wormhole can be visualized as a tunnel with two ends at separate points in spacetime (i.e., different locations, different points in time, or both). Wormholes are consistent with the General relativity, general theory of relativity, but whether wormholes actually exist remains to be seen. Many scientists postulate that wormholes are merely projections of a Four-dimensional space, fourth spatial dimension, analogous to how a two-dimensional (2D) being could experience only part of a three-dimensional (3D) object. Theoretically, a wormhole might connect extremely long distances such as a billion light years, or short distances such as a few meters, or different points in time, or even multiverse, different universes. In 1995, Matt Visser suggested there may be ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gravitational Singularity
A gravitational singularity, spacetime singularity or simply singularity is a condition in which gravitational field, gravity is so intense that spacetime itself breaks down catastrophically. As such, a singularity is by definition no longer part of the regular spacetime and cannot be determined by "where" or "when". Gravitational singularities exist at a junction between general relativity and quantum mechanics; therefore, the properties of the singularity cannot be described without an established theory of quantum gravity. Trying to find a complete and precise definition of singularities in the theory of general relativity, the current best theory of gravity, remains a difficult problem. A singularity in general relativity can be defined by the Curvature invariant (general relativity), scalar invariant Curvature of Riemannian manifolds, curvature becoming Infinity, infinite or, better, by a Geodesics in general relativity, geodesic being Geodesic manifold#Non-examples, incom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometrodynamics
In theoretical physics, geometrodynamics is an attempt to describe spacetime and associated phenomena completely in terms of geometry. Technically, its goal is to unify the fundamental forces and reformulate general relativity as a configuration space of three-metrics, modulo three-dimensional diffeomorphisms. The origin of this idea can be found in a English mathematician William Kingdon Clifford's works. Wheeler, John Archibald. 1962 960 "Curved empty space as the building material of the physical world: an assessment." In ''Logic, Methodology, and Philosophy of Science'', edited by E. Nagel. Stanford University Press. This theory was enthusiastically promoted by John Wheeler in the 1960s, and work on it continues in the 21st century. Einstein's geometrodynamics The term geometrodynamics is as a synonym for general relativity. More properly, some authors use the phrase ''Einstein's geometrodynamics'' to denote the initial value formulation of general relativity, intr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Spacetime
In mathematics and mathematical physics, complex spacetime extends the traditional notion of spacetime described by real-valued space and time coordinates to complex-valued space and time coordinates. The notion is entirely mathematical with no physics implied, but should be seen as a tool, for instance, as exemplified by the Wick rotation. Real and complex spaces Mathematics The complexification of a real vector space results in a complex vector space (over the complex number field). To "complexify" a space means extending ordinary scalar multiplication of vectors by real numbers to scalar multiplication by complex numbers. For complexified inner product spaces, the complex inner product on vectors replaces the ordinary real-valued inner product, an example of the latter being the dot product. In mathematical physics, when we complexify a real coordinate space \mathbb^n we create a complex coordinate space \mathbb^n, referred to in differential geometry as a "comple ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Closed Timelike Curve
In mathematical physics, a closed timelike curve (CTC) is a world line in a Lorentzian manifold, of a material particle in spacetime, that is "closed", returning to its starting point. This possibility was first discovered by Willem Jacob van Stockum in 1937 and later confirmed by Kurt Gödel in 1949,Stephen Hawking, '' My Brief History'', chapter 11 who discovered a solution to the equations of general relativity (GR) allowing CTCs known as the Gödel metric; and since then other GR solutions containing CTCs have been found, such as the Tipler cylinder and traversable wormholes. If CTCs exist, their existence would seem to imply at least the theoretical possibility of time travel backwards in time, raising the spectre of the grandfather paradox, although the Novikov self-consistency principle seems to show that such paradoxes could be avoided. Some physicists speculate that the CTCs which appear in certain GR solutions might be ruled out by a future theory of quantum gravity whic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aleksandr Danilovich Aleksandrov
Aleksandr Danilovich Aleksandrov (russian: Алекса́ндр Дани́лович Алекса́ндров, alternative transliterations: ''Alexandr'' or ''Alexander'' (first name), and ''Alexandrov'' (last name)) (4 August 1912 – 27 July 1999) was a Soviet/Russian mathematician, physicist, philosopher and mountaineer. Personal Life Aleksandr Aleksandrov was born in 1912 in Volyn, Ryazan Oblast. His father was a headmaster of a secondary school in St Petersburg and his mother a teacher at said school, thus the young Alekandrov spent a majority of his childhood in the city. His family was old Russian nobility—students noted ancestral portraits which hung in his office. His sisters were Soviet botanist Vera Danilovna Aleksandrov (RU) and Maria Danilovna Aleksandrova, author of the first monograph on gerontopsychology in the USSR. In 1937, he married a student of the Faculty of Physics, Marianna Leonidovna Georg. Together they had two children: Daria (b. 1948) and Daniil (R ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pavel Alexandrov
Pavel Sergeyevich Alexandrov (russian: Па́вел Серге́евич Алекса́ндров), sometimes romanized ''Paul Alexandroff'' (7 May 1896 – 16 November 1982), was a Soviet mathematician. He wrote about three hundred papers, making important contributions to set theory and topology. In topology, the Alexandroff compactification and the Alexandrov topology are named after him. Biography Alexandrov attended Moscow State University where he was a student of Dmitri Egorov and Nikolai Luzin. Together with Pavel Urysohn, he visited the University of Göttingen in 1923 and 1924. After getting his Ph.D. in 1927, he continued to work at Moscow State University and also joined the Steklov Institute of Mathematics. He was made a member of the Russian Academy of Sciences in 1953. Personal life Luzin challenged Alexandrov to determine if the continuum hypothesis is true. This still unsolved problem was too much for Alexandrov and he had a creative crisis at the end of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alexandrov Topology
In topology, an Alexandrov topology is a topology in which the intersection of any family of open sets is open. It is an axiom of topology that the intersection of any ''finite'' family of open sets is open; in Alexandrov topologies the finite restriction is dropped. A set together with an Alexandrov topology is known as an Alexandrov-discrete space or finitely generated space. Alexandrov topologies are uniquely determined by their specialization preorders. Indeed, given any preorder ≤ on a set ''X'', there is a unique Alexandrov topology on ''X'' for which the specialization preorder is ≤. The open sets are just the upper sets with respect to ≤. Thus, Alexandrov topologies on ''X'' are in one-to-one correspondence with preorders on ''X''. Alexandrov-discrete spaces are also called finitely generated spaces since their topology is uniquely determined by the family of all finite subspaces. Alexandrov-discrete spaces can thus be viewed as a generalization of finite topol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Causality Conditions
In the study of Lorentzian manifold spacetimes there exists a hierarchy of causality conditions which are important in proving mathematical theorems about the global structure of such manifolds. These conditions were collected during the late 1970s.E. Minguzzi and M. Sanchez, ''The causal hierarchy of spacetimes'' in H. Baum and D. Alekseevsky (eds.), vol. Recent developments in pseudo-Riemannian geometry, ESI Lect. Math. Phys., (Eur. Math. Soc. Publ. House, Zurich, 2008), pp. 299–358, , arXiv:gr-qc/0609119 The weaker the causality condition on a spacetime, the more ''unphysical'' the spacetime is. Spacetimes with closed timelike curves, for example, present severe interpretational difficulties. See the grandfather paradox. It is reasonable to believe that any physical spacetime will satisfy the strongest causality condition: global hyperbolicity. For such spacetimes the equations in general relativity can be posed as an initial value problem on a Cauchy surface. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
