|
Slow Light
Slow light is the propagation of an optical pulse or other modulation of an optical carrier at a very low group velocity. Slow light occurs when a propagating pulse is substantially slowed by the interaction with the medium in which the propagation takes place. Group velocities below c were known to be possible as far back as 1880, but could not be realized in a useful manner until 1991, when Stephen Harris and collaborators demonstrated electromagnetically induced transparency in trapped strontium atoms. Reduction of the speed of light by a factor of 165 was reported in 1995. In 1998, Danish physicist Lene Vestergaard Hau led a combined team from Harvard University and the Rowland Institute for Science which realized much lower group velocities of light. They succeeded in slowing a beam of light to about 17 meters per second. In 2004, researchers at UC Berkeley first demonstrated slow light in a semiconductor, with a group velocity 9.6 kilometers per second. Hau and her colle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Group Velocity
The group velocity of a wave is the velocity with which the overall envelope shape of the wave's amplitudes—known as the ''modulation'' or ''envelope'' of the wave—propagates through space. For example, if a stone is thrown into the middle of a very still pond, a circular pattern of waves with a quiescent center appears in the water, also known as a capillary wave. The expanding ring of waves is the wave group, within which one can discern individual waves that travel faster than the group as a whole. The amplitudes of the individual waves grow as they emerge from the trailing edge of the group and diminish as they approach the leading edge of the group. Definition and interpretation Definition The group velocity is defined by the equation: :v_ \ \equiv\ \frac\, where is the wave's angular frequency (usually expressed in radians per second), and is the angular wavenumber (usually expressed in radians per meter). The phase velocity is: . The function , which gi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maxwell's Equations
Maxwell's equations, or Maxwell–Heaviside equations, are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, and electric circuits. The equations provide a mathematical model for electric, optical, and radio technologies, such as power generation, electric motors, wireless communication, lenses, radar etc. They describe how electric field, electric and magnetic fields are generated by electric charge, charges, electric current, currents, and changes of the fields.''Electric'' and ''magnetic'' fields, according to the theory of relativity, are the components of a single electromagnetic field. The equations are named after the physicist and mathematician James Clerk Maxwell, who, in 1861 and 1862, published an early form of the equations that included the Lorentz force law. Maxwell first used the equations to propose that light is an electromagnetic phenomenon. The modern f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. For example, the derivative of the position of a moving object with respect to time is the object's velocity: this measures how quickly the position of the object changes when time advances. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the "instantaneous rate of change", the ratio of the instantaneous change in the dependent variable to that of the independent variable. Derivatives can be generalized to functions of several real variables. In this generalization, the deriv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Color
Color (American English) or colour (British English) is the visual perceptual property deriving from the spectrum of light interacting with the photoreceptor cells of the eyes. Color categories and physical specifications of color are associated with objects or materials based on their physical properties such as light absorption, reflection, or emission spectra. By defining a color space, colors can be identified numerically by their coordinates. Because perception of color stems from the varying spectral sensitivity of different types of cone cells in the retina to different parts of the spectrum, colors may be defined and quantified by the degree to which they stimulate these cells. These physical or physiological quantifications of color, however, do not fully explain the psychophysical perception of color appearance. Color science includes the perception of color by the eye and brain, the origin of color in materials, color theory in art, and the physics of ele ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brightness
Brightness is an attribute of visual perception in which a source appears to be radiating or reflecting light. In other words, brightness is the perception elicited by the luminance of a visual target. The perception is not linear to luminance, and relies on the context of the viewing environment (for example, see White's illusion). Brightness is a subjective sensation of an object being observed and one of the color appearance parameters of many color appearance models, typically denoted as Q. Brightness refers to how much light ''appears to shine'' from something. This is a different perception than lightness, which is how light something appears ''compared to'' a similarly lit white object. The adjective ''bright'' derives from an Old English ''beorht'' with the same meaning via metathesis giving Middle English ''briht''. The word is from a Common Germanic ', ultimately from a PIE root with a closely related meaning, *' "white, bright". "Brightness" was formerly used as a s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Luminous Intensity
In photometry, luminous intensity is a measure of the wavelength-weighted power emitted by a light source in a particular direction per unit solid angle, based on the luminosity function, a standardized model of the sensitivity of the human eye. The SI unit of luminous intensity is the candela (cd), an SI base unit. Measurement Photometry deals with the measurement of visible light as perceived by human eyes. The human eye can only see light in the visible spectrum and has different sensitivities to light of different wavelengths within the spectrum. When adapted for bright conditions (photopic vision), the eye is most sensitive to yellow-green light at 555 nm. Light with the same radiant intensity at other wavelengths has a lower luminous intensity. The curve which measures the response of the human eye to light is a defined standard, known as the luminosity function. This curve, denoted ''V''(λ) or \textstyle \overline(\lambda), is based on an average of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
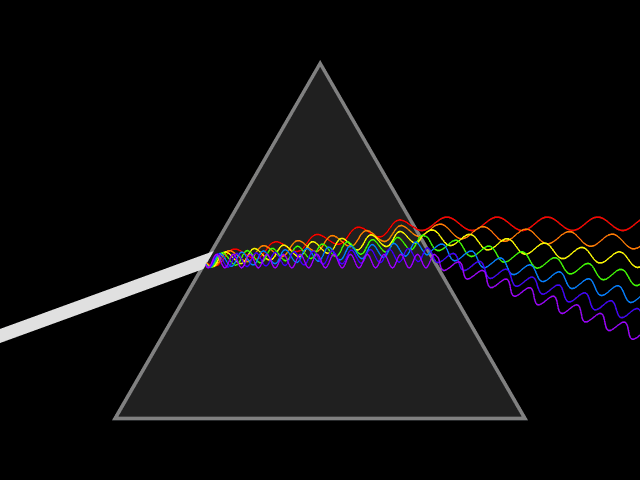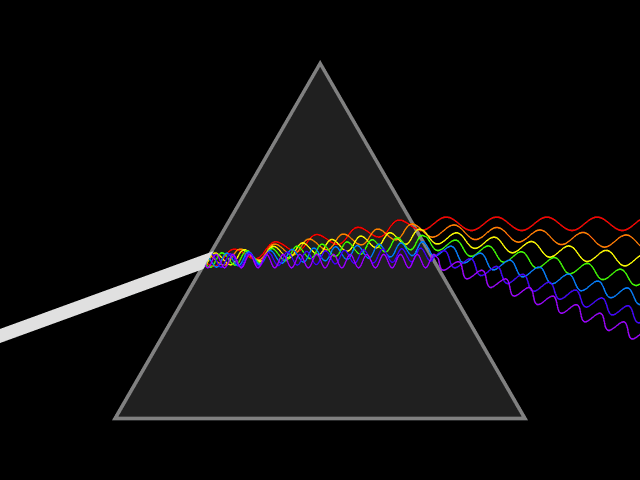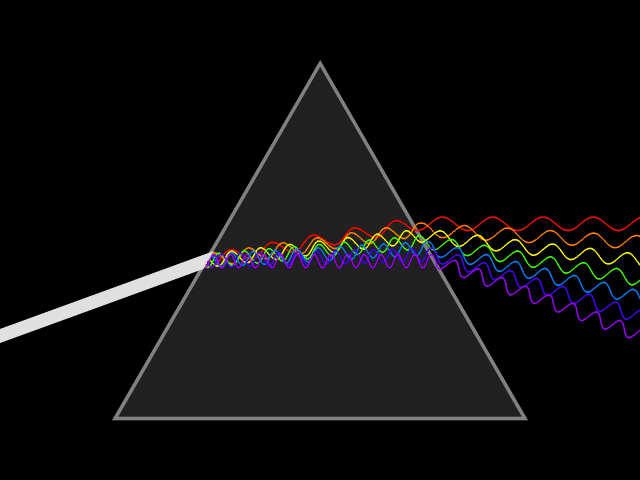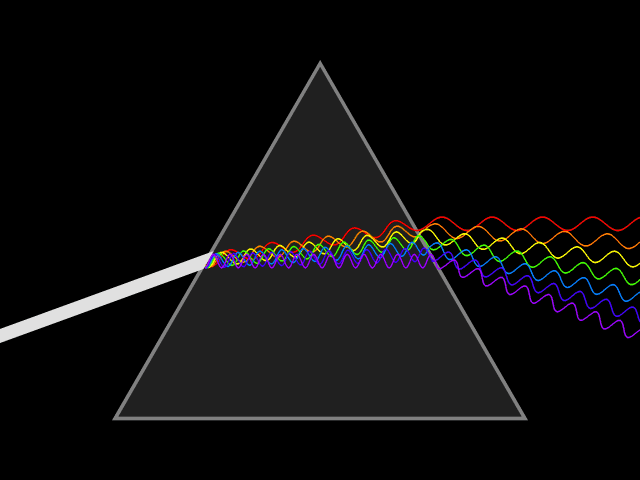
Dispersion (optics)
In optics, and by analogy other branches of physics dealing with wave propagation, dispersion is the phenomenon in which the phase velocity of a wave depends on its frequency; sometimes the term chromatic dispersion is used for specificity to optics in particular. A medium having this common property may be termed a dispersive medium (plural ''dispersive media''). Although the term is used in the field of optics to describe light and other electromagnetic waves, dispersion in the same sense can apply to any sort of wave motion such as acoustic dispersion in the case of sound and seismic waves, and in gravity waves (ocean waves). Within optics, dispersion is a property of telecommunication signals along transmission lines (such as microwaves in coaxial cable) or the pulses of light in optical fiber. Physically, dispersion translates in a loss of kinetic energy through absorption. In optics, one important and familiar consequence of dispersion is the change in the angle of refra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Index Of Refraction
In optics, the refractive index (or refraction index) of an optical medium is a dimensionless number that gives the indication of the light bending ability of that medium. The refractive index determines how much the path of light is bent, or refracted, when entering a material. This is described by Snell's law of refraction, , where ''θ''1 and ''θ''2 are the angle of incidence and angle of refraction, respectively, of a ray crossing the interface between two media with refractive indices ''n''1 and ''n''2. The refractive indices also determine the amount of light that is reflected when reaching the interface, as well as the critical angle for total internal reflection, their intensity (Fresnel's equations) and Brewster's angle. The refractive index can be seen as the factor by which the speed and the wavelength of the radiation are reduced with respect to their vacuum values: the speed of light in a medium is , and similarly the wavelength in that medium is , where ''λ''0 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sinusoidal
A sine wave, sinusoidal wave, or just sinusoid is a mathematical curve defined in terms of the '' sine'' trigonometric function, of which it is the graph. It is a type of continuous wave and also a smooth periodic function. It occurs often in mathematics, as well as in physics, engineering, signal processing and many other fields. Formulation Its most basic form as a function of time (''t'') is: y(t) = A\sin(2 \pi f t + \varphi) = A\sin(\omega t + \varphi) where: * ''A'', ''amplitude'', the peak deviation of the function from zero. * ''f'', '' ordinary frequency'', the ''number'' of oscillations (cycles) that occur each second of time. * ''ω'' = 2''f'', '' angular frequency'', the rate of change of the function argument in units of radians per second. * \varphi, '' phase'', specifies (in radians) where in its cycle the oscillation is at ''t'' = 0. When \varphi is non-zero, the entire waveform appears to be shifted in time by the amount ''φ''/''ω'' seconds. A negative val ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ampère's Force Law
In magnetostatics, the force of attraction or repulsion between two current-carrying wires (see first figure below) is often called Ampère's force law. The physical origin of this force is that each wire generates a magnetic field, following the Biot–Savart law, and the other wire experiences a magnetic force as a consequence, following the Lorentz force law. Equation Special case: Two straight parallel wires The best-known and simplest example of Ampère's force law, which underlaid (before 20 May 2019) the definition of the ampere, the SI unit of current, states that the magnetic force per unit length between two straight parallel conductors is \frac = 2 k_ \frac , where k_ is the magnetic force constant from the Biot–Savart law, F_m / L is the total force on either wire per unit length of the shorter (the longer is approximated as infinitely long relative to the shorter), r is the distance between the two wires, and I_1, I_2 are the direct currents carri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gauss' Law
In physics and electromagnetism, Gauss's law, also known as Gauss's flux theorem, (or sometimes simply called Gauss's theorem) is a law relating the distribution of electric charge to the resulting electric field. In its integral form, it states that the flux of the electric field out of an arbitrary closed surface is proportional to the electric charge enclosed by the surface, irrespective of how that charge is distributed. Even though the law alone is insufficient to determine the electric field across a surface enclosing any charge distribution, this may be possible in cases where symmetry mandates uniformity of the field. Where no such symmetry exists, Gauss's law can be used in its differential form, which states that the divergence of the electric field is proportional to the local density of charge. The law was first formulated by Joseph-Louis Lagrange in 1773, followed by Carl Friedrich Gauss in 1835, both in the context of the attraction of ellipsoids. It is one ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lorentz Force
In physics (specifically in electromagnetism) the Lorentz force (or electromagnetic force) is the combination of electric and magnetic force on a point charge due to electromagnetic fields. A particle of charge moving with a velocity in an electric field and a magnetic field experiences a force of \mathbf = q\,\mathbf + q\,\mathbf \times \mathbf (in SI unitsIn SI units, is measured in teslas (symbol: T). In Gaussian-cgs units, is measured in gauss (symbol: G). See e.g. )The -field is measured in amperes per metre (A/m) in SI units, and in oersteds (Oe) in cgs units. ). It says that the electromagnetic force on a charge is a combination of a force in the direction of the electric field proportional to the magnitude of the field and the quantity of charge, and a force at right angles to the magnetic field and the velocity of the charge, proportional to the magnitude of the field, the charge, and the velocity. Variations on this basic formula describe the magnetic forc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.gif)