|
Sextic
In algebra, a sextic (or hexic) polynomial is a polynomial of degree six. A sextic equation is a polynomial equation of degree six—that is, an equation whose left hand side is a sextic polynomial and whose right hand side is zero. More precisely, it has the form: :ax^6+bx^5+cx^4+dx^3+ex^2+fx+g=0,\, where and the ''coefficients'' may be integers, rational numbers, real numbers, complex numbers or, more generally, members of any field. A sextic function is a function defined by a sextic polynomial. Because they have an even degree, sextic functions appear similar to quartic functions when graphed, except they may possess an additional local maximum and local minimum each. The derivative of a sextic function is a quintic function. Since a sextic function is defined by a polynomial with even degree, it has the same infinite limit when the argument goes to positive or negative infinity. If the leading coefficient is positive, then the function increases to positive infinity ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kampé De Fériet Function
In mathematics, the Kampé de Fériet function is a two-variable generalization of the generalized hypergeometric series, introduced by Joseph Kampé de Fériet Marie-Joseph Kampé de Fériet ( Paris, 14 May 1893 – Villeneuve d'Ascq, 6 April 1982) was professor at Université Lille Nord de France from 1919 to 1969. Besides his works on mathematics and fluid mechanics, he directed the ''Institut de .... The Kampé de Fériet function is given by : ^F_\left( \begin a_1,\cdots,a_p\colon b_1,b_1';\cdots;b_q,b_q'; \\ c_1,\cdots,c_r\colon d_1,d_1';\cdots;d_s,d_s'; \end x,y\right)= \sum_^\infty\sum_^\infty\frac\frac\cdot\frac. Applications The general sextic equation can be solved in terms of Kampé de Fériet functions. References * * * External links * Hypergeometric functions {{analysis-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quintic Equation
In algebra, a quintic function is a function of the form :g(x)=ax^5+bx^4+cx^3+dx^2+ex+f,\, where , , , , and are members of a field, typically the rational numbers, the real numbers or the complex numbers, and is nonzero. In other words, a quintic function is defined by a polynomial of degree five. Because they have an odd degree, normal quintic functions appear similar to normal cubic functions when graphed, except they may possess one additional local maximum and one additional local minimum. The derivative of a quintic function is a quartic function. Setting and assuming produces a quintic equation of the form: :ax^5+bx^4+cx^3+dx^2+ex+f=0.\, Solving quintic equations in terms of radicals (''n''th roots) was a major problem in algebra from the 16th century, when cubic and quartic equations were solved, until the first half of the 19th century, when the impossibility of such a general solution was proved with the Abel–Ruffini theorem. Finding roots of a quintic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quintic Function
In algebra, a quintic function is a function of the form :g(x)=ax^5+bx^4+cx^3+dx^2+ex+f,\, where , , , , and are members of a field, typically the rational numbers, the real numbers or the complex numbers, and is nonzero. In other words, a quintic function is defined by a polynomial of degree five. Because they have an odd degree, normal quintic functions appear similar to normal cubic functions when graphed, except they may possess one additional local maximum and one additional local minimum. The derivative of a quintic function is a quartic function. Setting and assuming produces a quintic equation of the form: :ax^5+bx^4+cx^3+dx^2+ex+f=0.\, Solving quintic equations in terms of radicals (''n''th roots) was a major problem in algebra from the 16th century, when cubic and quartic equations were solved, until the first half of the 19th century, when the impossibility of such a general solution was proved with the Abel–Ruffini theorem. Finding roots of a quintic equa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
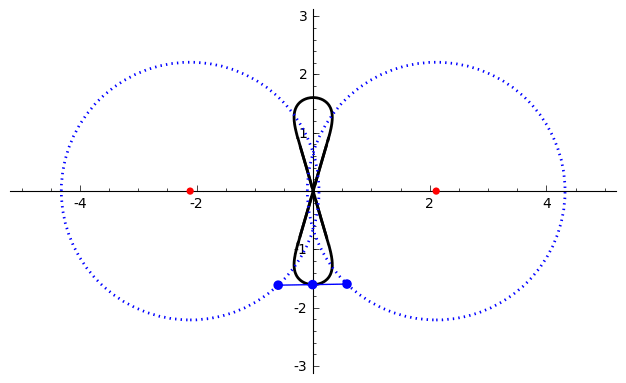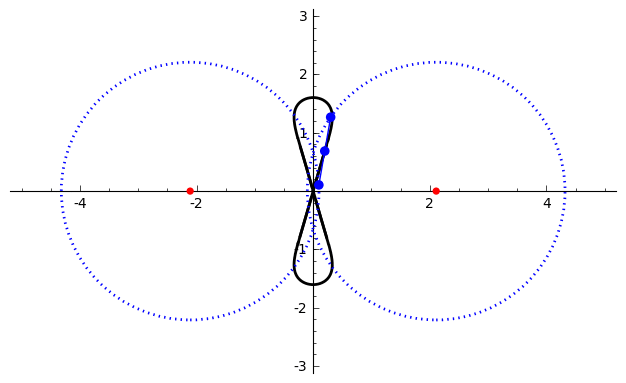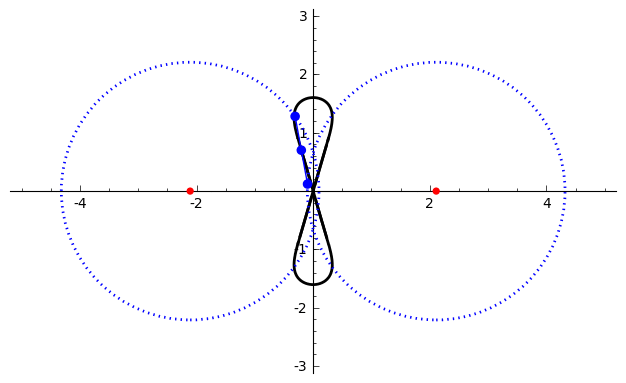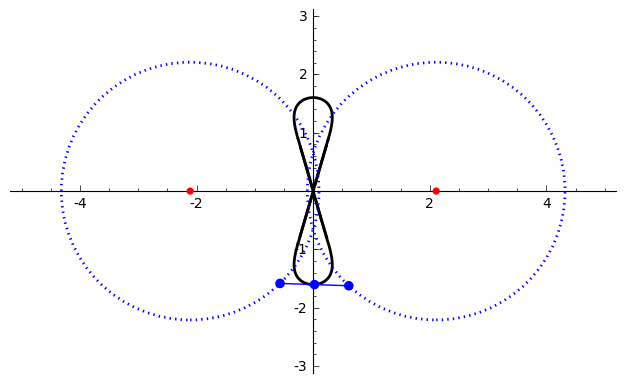
Watt's Curve
In mathematics, Watt's curve is a tricircular plane algebraic curve of degree six. It is generated by two circles of radius ''b'' with centers distance 2''a'' apart (taken to be at (±''a'', 0)). A line segment of length 2''c'' attaches to a point on each of the circles, and the midpoint of the line segment traces out the Watt curve as the circles rotate partially back and forth or completely around. It arose in connection with James Watt's pioneering work on the steam engine. The equation of the curve can be given in polar coordinates as :r^2=b^2-\left \sin\theta\pm\sqrt\right2. Derivation Polar coordinates The polar equation for the curve can be derived as follows: Working in the complex plane, let the centers of the circles be at ''a'' and ''−a'', and the connecting segment have endpoints at ''−a''+''be''''i'' λ and ''a''+''be''''i'' ρ. Let the angle of inclination of the segment be ψ with its midpoint at ''re''''i'' θ. Then the endpoints are also given by '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polynomial
In mathematics, a polynomial is an expression consisting of indeterminates (also called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An example of a polynomial of a single indeterminate is . An example with three indeterminates is . Polynomials appear in many areas of mathematics and science. For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problems to complicated scientific problems; they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics and social science; they are used in calculus and numerical analysis to approximate other functions. In advanced mathematics, polynomials are used to construct polynomial rings and algebraic varieties, which are central concepts in algebra and algebraic geometry. Etymology The word ''polynomial'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polynomial Equation
In mathematics, an algebraic equation or polynomial equation is an equation of the form :P = 0 where ''P'' is a polynomial with coefficients in some field, often the field of the rational numbers. For many authors, the term ''algebraic equation'' refers only to ''univariate equations'', that is polynomial equations that involve only one variable. On the other hand, a polynomial equation may involve several variables. In the case of several variables (the ''multivariate'' case), the term ''polynomial equation'' is usually preferred to ''algebraic equation''. For example, :x^5-3x+1=0 is an algebraic equation with integer coefficients and :y^4 + \frac - \frac + xy^2 + y^2 + \frac = 0 is a multivariate polynomial equation over the rationals. Some but not all polynomial equations with rational coefficients have a solution that is an algebraic expression that can be found using a finite number of operations that involve only those same types of coefficients (that is, can be so ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Latin
Latin (, or , ) is a classical language belonging to the Italic branch of the Indo-European languages. Latin was originally a dialect spoken in the lower Tiber area (then known as Latium) around present-day Rome, but through the power of the Roman Republic it became the dominant language in the Italian region and subsequently throughout the Roman Empire. Even after the fall of Western Rome, Latin remained the common language of international communication, science, scholarship and academia in Europe until well into the 18th century, when other regional vernaculars (including its own descendants, the Romance languages) supplanted it in common academic and political usage, and it eventually became a dead language in the modern linguistic definition. Latin is a highly inflected language, with three distinct genders (masculine, feminine, and neuter), six or seven noun cases (nominative, accusative, genitive, dative, ablative, and vocative), five declensions, four ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cubic Function
In mathematics, a cubic function is a function of the form f(x)=ax^3+bx^2+cx+d where the coefficients , , , and are complex numbers, and the variable takes real values, and a\neq 0. In other words, it is both a polynomial function of degree three, and a real function. In particular, the domain and the codomain are the set of the real numbers. Setting produces a cubic equation of the form :ax^3+bx^2+cx+d=0, whose solutions are called roots of the function. A cubic function has either one or three real roots (which may not be distinct); all odd-degree polynomials have at least one real root. The graph of a cubic function always has a single inflection point. It may have two critical points, a local minimum and a local maximum. Otherwise, a cubic function is monotonic. The graph of a cubic function is symmetric with respect to its inflection point; that is, it is invariant under a rotation of a half turn around this point. Up to an affine transformation, there are o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Steam Engine
A steam engine is a heat engine that performs mechanical work using steam as its working fluid. The steam engine uses the force produced by steam pressure to push a piston back and forth inside a cylinder. This pushing force can be transformed, by a connecting rod and crank, into rotational force for work. The term "steam engine" is generally applied only to reciprocating engines as just described, not to the steam turbine. Steam engines are external combustion engines, where the working fluid is separated from the combustion products. The ideal thermodynamic cycle used to analyze this process is called the Rankine cycle. In general usage, the term ''steam engine'' can refer to either complete steam plants (including boilers etc.), such as railway steam locomotives and portable engines, or may refer to the piston or turbine machinery alone, as in the beam engine and stationary steam engine. Although steam-driven devices were known as early as the aeo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Évariste Galois
Évariste Galois (; ; 25 October 1811 – 31 May 1832) was a French mathematician and political activist. While still in his teens, he was able to determine a necessary and sufficient condition for a polynomial to be solvable by radicals, thereby solving a problem that had been open for 350 years. His work laid the foundations for Galois theory and group theory, two major branches of abstract algebra. He was a staunch republican and was heavily involved in the political turmoil that surrounded the French Revolution of 1830. As a result of his political activism, he was arrested repeatedly, serving one jail sentence of several months. For reasons that remain obscure, shortly after his release from prison he fought in a duel and died of the wounds he suffered. Life Early life Galois was born on 25 October 1811 to Nicolas-Gabriel Galois and Adélaïde-Marie (née Demante). His father was a Republican and was head of Bourg-la-Reine's liberal party. His father became ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Felix Klein
Christian Felix Klein (; 25 April 1849 – 22 June 1925) was a German mathematician and mathematics educator, known for his work with group theory, complex analysis, non-Euclidean geometry, and on the associations between geometry and group theory. His 1872 Erlangen program, classifying geometries by their basic symmetry groups, was an influential synthesis of much of the mathematics of the time. Life Felix Klein was born on 25 April 1849 in Düsseldorf, to Prussian parents. His father, Caspar Klein (1809–1889), was a Prussian government official's secretary stationed in the Rhine Province. His mother was Sophie Elise Klein (1819–1890, née Kayser). He attended the Gymnasium in Düsseldorf, then studied mathematics and physics at the University of Bonn, 1865–1866, intending to become a physicist. At that time, Julius Plücker had Bonn's professorship of mathematics and experimental physics, but by the time Klein became his assistant, in 1866, Plücker's interes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |