|
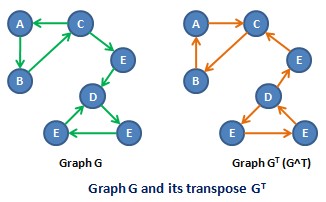
Reverse Graph
In the mathematical and algorithmic study of graph theory, the converse, transpose or reverse, entry 2.24 of a directed graph is another directed graph on the same set of vertices with all of the edges reversed compared to the orientation of the corresponding edges in . That is, if contains an edge then the converse/transpose/reverse of contains an edge and vice versa. Notation The name arises because the reversal of arrows corresponds to taking the converse of an implication in logic. The name is because the adjacency matrix of the transpose directed graph is the transpose of the adjacency matrix of the original directed graph. There is no general agreement on preferred terminology. The converse is denoted symbolically as , , , or other notations, depending on which terminology is used and which book or article is the source for the notation. Applications Although there is little difference mathematically between a graph and its transpose, the difference may be lar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strongly Connected Component
In the mathematical theory of directed graphs, a graph is said to be strongly connected if every vertex is reachable from every other vertex. The strongly connected components of an arbitrary directed graph form a partition into subgraphs that are themselves strongly connected. It is possible to test the strong connectivity of a graph, or to find its strongly connected components, in linear time (that is, Θ(''V'' + ''E'')). Definitions A directed graph is called strongly connected if there is a path in each direction between each pair of vertices of the graph. That is, a path exists from the first vertex in the pair to the second, and another path exists from the second vertex to the first. In a directed graph ''G'' that may not itself be strongly connected, a pair of vertices ''u'' and ''v'' are said to be strongly connected to each other if there is a path in each direction between them. The binary relation of being strongly connected is an equivalence relation, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Directed Acyclic Graph
In mathematics, particularly graph theory, and computer science, a directed acyclic graph (DAG) is a directed graph with no directed cycles. That is, it consists of vertices and edges (also called ''arcs''), with each edge directed from one vertex to another, such that following those directions will never form a closed loop. A directed graph is a DAG if and only if it can be topologically ordered, by arranging the vertices as a linear ordering that is consistent with all edge directions. DAGs have numerous scientific and computational applications, ranging from biology (evolution, family trees, epidemiology) to information science (citation networks) to computation (scheduling). Directed acyclic graphs are sometimes instead called acyclic directed graphs or acyclic digraphs. Definitions A graph is formed by vertices and by edges connecting pairs of vertices, where the vertices can be any kind of object that is connected in pairs by edges. In the case of a directed graph, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transitive Closure
In mathematics, the transitive closure of a binary relation on a set is the smallest relation on that contains and is transitive. For finite sets, "smallest" can be taken in its usual sense, of having the fewest related pairs; for infinite sets it is the unique minimal transitive superset of . For example, if is a set of airports and means "there is a direct flight from airport to airport " (for and in ), then the transitive closure of on is the relation such that means "it is possible to fly from to in one or more flights". Informally, the ''transitive closure'' gives you the set of all places you can get to from any starting place. More formally, the transitive closure of a binary relation on a set is the transitive relation on set such that contains and is minimal; see . If the binary relation itself is transitive, then the transitive closure is that same binary relation; otherwise, the transitive closure is a different relation. Conversely, transitive ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Order
In mathematics, especially order theory, a partially ordered set (also poset) formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation indicating that, for certain pairs of elements in the set, one of the elements precedes the other in the ordering. The relation itself is called a "partial order." The word ''partial'' in the names "partial order" and "partially ordered set" is used as an indication that not every pair of elements needs to be comparable. That is, there may be pairs of elements for which neither element precedes the other in the poset. Partial orders thus generalize total orders, in which every pair is comparable. Informal definition A partial order defines a notion of comparison. Two elements ''x'' and ''y'' may stand in any of four mutually exclusive relationships to each other: either ''x'' ''y'', or ''x'' and ''y'' are ''incompar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Duality (order Theory)
In the mathematical area of order theory, every partially ordered set ''P'' gives rise to a dual (or opposite) partially ordered set which is often denoted by ''P''op or ''P''''d''. This dual order ''P''op is defined to be the same set, but with the inverse order, i.e. ''x'' ≤ ''y'' holds in ''P''op if and only if ''y'' ≤ ''x'' holds in ''P''. It is easy to see that this construction, which can be depicted by flipping the Hasse diagram for ''P'' upside down, will indeed yield a partially ordered set. In a broader sense, two partially ordered sets are also said to be duals if they are dually isomorphic, i.e. if one poset is order isomorphic to the dual of the other. The importance of this simple definition stems from the fact that every definition and theorem of order theory can readily be transferred to the dual order. Formally, this is captured by the Duality Principle for ordered sets: : If a given statement is valid for all partially ordered sets, then its dual statement, o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binary Relation
In mathematics, a binary relation associates elements of one set, called the ''domain'', with elements of another set, called the ''codomain''. A binary relation over Set (mathematics), sets and is a new set of ordered pairs consisting of elements in and in . It is a generalization of the more widely understood idea of a unary function. It encodes the common concept of relation: an element is ''related'' to an element , if and only if the pair belongs to the set of ordered pairs that defines the ''binary relation''. A binary relation is the most studied special case of an Finitary relation, -ary relation over sets , which is a subset of the Cartesian product X_1 \times \cdots \times X_n. An example of a binary relation is the "divides" relation over the set of prime numbers \mathbb and the set of integers \mathbb, in which each prime is related to each integer that is a Divisibility, multiple of , but not to an integer that is not a multiple of . In this relation, for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Converse Relation
In mathematics, the converse relation, or transpose, of a binary relation is the relation that occurs when the order of the elements is switched in the relation. For example, the converse of the relation 'child of' is the relation 'parent of'. In formal terms, if X and Y are sets and L \subseteq X \times Y is a relation from X to Y, then L^ is the relation defined so that yL^x if and only if xLy. In set-builder notation, :L^ = \. The notation is analogous with that for an inverse function. Although many functions do not have an inverse, every relation does have a unique converse. The unary operation that maps a relation to the converse relation is an involution, so it induces the structure of a semigroup with involution on the binary relations on a set, or, more generally, induces a dagger category on the category of relations as detailed below. As a unary operation, taking the converse (sometimes called conversion or transposition) commutes with the order-relate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Isomorphism
In graph theory, an isomorphism of graphs ''G'' and ''H'' is a bijection between the vertex sets of ''G'' and ''H'' : f \colon V(G) \to V(H) such that any two vertices ''u'' and ''v'' of ''G'' are adjacent in ''G'' if and only if f(u) and f(v) are adjacent in ''H''. This kind of bijection is commonly described as "edge-preserving bijection", in accordance with the general notion of isomorphism being a structure-preserving bijection. If an isomorphism exists between two graphs, then the graphs are called isomorphic and denoted as G\simeq H. In the case when the bijection is a mapping of a graph onto itself, i.e., when ''G'' and ''H'' are one and the same graph, the bijection is called an automorphism of ''G''. If a graph is finite, we can prove it to be bijective by showing it is one-one/onto; no need to show both. Graph isomorphism is an equivalence relation on graphs and as such it partitions the class of all graphs into equivalence classes. A set of graphs isomorphic to each ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Skew-symmetric Graph
In graph theory, a branch of mathematics, a skew-symmetric graph is a directed graph that is isomorphic to its own transpose graph, the graph formed by reversing all of its edges, under an isomorphism that is an involution without any fixed points. Skew-symmetric graphs are identical to the double covering graphs of bidirected graphs. Skew-symmetric graphs were first introduced under the name of ''antisymmetrical digraphs'' by , later as the double covering graphs of polar graphs by , and still later as the double covering graphs of bidirected graphs by . They arise in modeling the search for alternating paths and alternating cycles in algorithms for finding matchings in graphs, in testing whether a still life pattern in Conway's Game of Life may be partitioned into simpler components, in graph drawing, and in the implication graphs used to efficiently solve the 2-satisfiability problem. Definition As defined, e.g., by , a skew-symmetric graph ''G'' is a directed graph, toget ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Depth-first Search
Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible along each branch before backtracking. Extra memory, usually a stack, is needed to keep track of the nodes discovered so far along a specified branch which helps in backtracking of the graph. A version of depth-first search was investigated in the 19th century by French mathematician Charles Pierre Trémaux as a strategy for solving mazes. Properties The time and space analysis of DFS differs according to its application area. In theoretical computer science, DFS is typically used to traverse an entire graph, and takes time where , V, is the number of vertices and , E, the number of edges. This is linear in the size of the graph. In these applications it also uses space O(, V, ) in the worst case to store the stack of vertices on th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kosaraju's Algorithm
In computer science, Kosaraju-Sharir's algorithm (also known as Kosaraju's algorithm) is a linear time algorithm to find the strongly connected components of a directed graph. Aho, Hopcroft and Ullman credit it to S. Rao Kosaraju and Micha Sharir. Kosaraju suggested it in 1978 but did not publish it, while Sharir independently discovered it and published it in 1981. It makes use of the fact that the transpose graph (the same graph with the direction of every edge reversed) has exactly the same strongly connected components as the original graph. The algorithm The primitive graph operations that the algorithm uses are to enumerate the vertices of the graph, to store data per vertex (if not in the graph data structure itself, then in some table that can use vertices as indices), to enumerate the out-neighbours of a vertex (traverse edges in the forward direction), and to enumerate the in-neighbours of a vertex (traverse edges in the backward direction); however the last can be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |