|
Restricted Open-shell Hartree–Fock
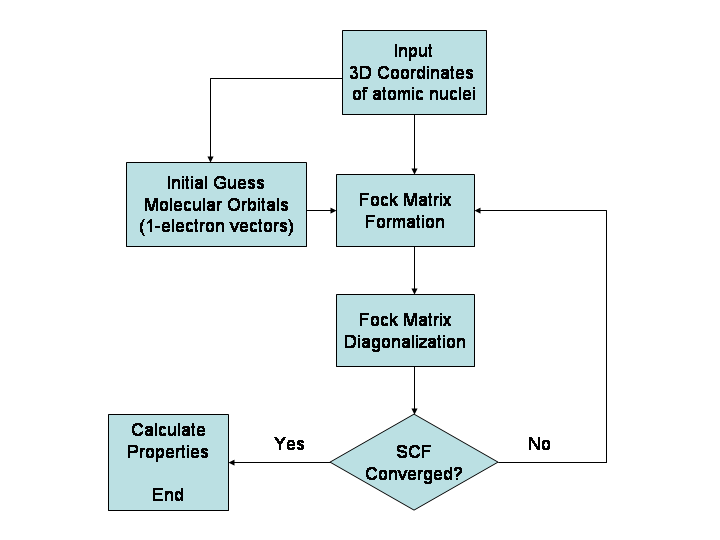
Restricted open-shell Hartree–Fock (ROHF) is a variant of Hartree–Fock method for open shell molecules. It uses doubly occupied molecular orbitals as far as possible and then singly occupied orbitals for the unpaired electrons. This is the simple picture for open shell molecules but it is difficult to implement. The foundations of the ROHF method were first formulated by Clemens C. J. Roothaan in a celebrated paper and then extended by various authors, see e.g. for in-depth discussions. As with restricted Hartree–Fock theory for closed shell molecules, it leads to Roothaan equations written in the form of a generalized eigenvalue problem :\mathbf \mathbf = \mathbf \mathbf \mathbf where \mathbf is the so-called Fock matrix (which is a function of \mathbf), \mathbf is a matrix of coefficients, \mathbf is the overlap matrix of the basis functions, and \epsilon is the (diagonal, by convention) matrix of orbital energies. Unlike restricted Hartree–Fock theory for closed shell ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hartree–Fock Method
In computational physics and chemistry, the Hartree–Fock (HF) method is a method of approximation for the determination of the wave function and the energy of a quantum many-body system in a stationary state. The method is named after Douglas Hartree and Vladimir Fock. The Hartree–Fock method often assumes that the exact ''N''-body wave function of the system can be approximated by a single Slater determinant (in the case where the particles are fermions) or by a single permanent (in the case of bosons) of ''N'' spin-orbitals. By invoking the variational method, one can derive a set of ''N''-coupled equations for the ''N'' spin orbitals. A solution of these equations yields the Hartree–Fock wave function and energy of the system. Hartree–Fock approximation is an instance of mean-field theory, where neglecting higher-order fluctuations in order parameter allows interaction terms to be replaced with quadratic terms, obtaining exactly solvable Hamiltonians. Especially ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Open Shell
In atomic physics and quantum chemistry, the electron configuration is the distribution of electrons of an atom or molecule (or other physical structure) in atomic or molecular orbitals. For example, the electron configuration of the neon atom is , meaning that the 1s, 2s, and 2p subshells are occupied by two, two, and six electrons, respectively. Electronic configurations describe each electron as moving independently in an orbital, in an average field created by the nuclei and all the other electrons. Mathematically, configurations are described by Slater determinants or configuration state functions. According to the laws of quantum mechanics, a level of energy is associated with each electron configuration. In certain conditions, electrons are able to move from one configuration to another by the emission or absorption of a quantum of energy, in the form of a photon. Knowledge of the electron configuration of different atoms is useful in understanding the structure o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
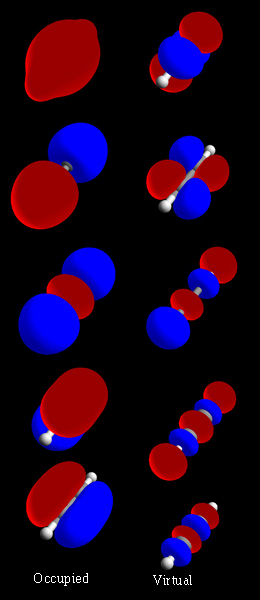
Molecular Orbitals
In chemistry, a molecular orbital is a mathematical function describing the location and wave-like behavior of an electron in a molecule. This function can be used to calculate chemical and physical properties such as the probability of finding an electron in any specific region. The terms ''atomic orbital'' and ''molecular orbital'' were introduced by Robert S. Mulliken in 1932 to mean ''one-electron orbital wave functions''. At an elementary level, they are used to describe the ''region'' of space in which a function has a significant amplitude. In an isolated atom, the orbital electrons' location is determined by functions called atomic orbitals. When multiple atoms combine chemically into a molecule by forming a valence chemical bond, the electrons' locations are determined by the molecule as a whole, so the atomic orbitals combine to form molecular orbitals. The electrons from the constituent atoms occupy the molecular orbitals. Mathematically, molecular orbitals are an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Clemens C
Clemens is a Late Latin, German, and Dutch masculine given name and a surname, meaning "merciful". Notable people with the name include: Surname * Adelaide Clemens (born 1989), Australian actress * Andrew Clemens (1857–1894), American folk artist * Aurelius Prudentius Clemens, 4th century Roman poet * Avery Jae Clemens, Australian model and social media influencer * Barry Clemens (born 1943), American basketball player * Bert A. Clemens (1874–1935), American politician * Brian Clemens (1931–2015), British screenwriter and television producer * Clayton Clemens, American Professor of Government * Christopher Clemens, American astronomer * Dan Clemens (1945–2019), American politician * Gabriel Clemens (born 1983), German darts player * George T. Clemens (1902–1992), American cinematographer * Harold W. Clemens (1918–1998), American politician * C. Herbert Clemens (born 1939), American mathematician * Isaac Clemens (1815–1880), Canadian farmer and politician * J ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Roothaan Equations
The Roothaan equations are a representation of the Hartree–Fock equation in a non orthonormal basis set which can be of Gaussian-type or Slater-type. It applies to closed-shell molecules or atoms where all molecular orbitals or atomic orbitals, respectively, are doubly occupied. This is generally called Restricted Hartree–Fock theory. The method was developed independently by Clemens C. J. Roothaan and George G. Hall in 1951, and is thus sometimes called the ''Roothaan-Hall equations''. The Roothaan equations can be written in a form resembling generalized eigenvalue problem, although they are not a standard eigenvalue problem because they are nonlinear: :\mathbf \mathbf = \mathbf \mathbf \mathbf where F is the Fock matrix (which depends on the coefficients C due to electron-electron interactions), C is a matrix of coefficients, S is the overlap matrix of the basis functions, and \epsilon is the (diagonal, by convention) matrix of orbital energies. In the case of an orth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Generalized Eigenvalue Problem
In linear algebra, eigendecomposition is the factorization of a matrix into a canonical form, whereby the matrix is represented in terms of its eigenvalues and eigenvectors. Only diagonalizable matrices can be factorized in this way. When the matrix being factorized is a normal or real symmetric matrix, the decomposition is called "spectral decomposition", derived from the spectral theorem. Fundamental theory of matrix eigenvectors and eigenvalues A (nonzero) vector of dimension is an eigenvector of a square matrix if it satisfies a linear equation of the form \mathbf \mathbf = \lambda \mathbf for some scalar . Then is called the eigenvalue corresponding to . Geometrically speaking, the eigenvectors of are the vectors that merely elongates or shrinks, and the amount that they elongate/shrink by is the eigenvalue. The above equation is called the eigenvalue equation or the eigenvalue problem. This yields an equation for the eigenvalues p\left(\lambda\right) = \det\lef ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Fock Matrix
The Fock matrix is defined by the Fock operator. In its general form the Fock operator writes: :\hat F(i) = \hat h(i)+\sum_^ hat J_j(i)-\hat K_j(i)/math> Where ''i'' runs over the total ''N'' spin orbitals. In the closed-shell case, it can be simplified by considering only the spatial orbitals. Noting that the \hat J terms are duplicated and the exchange terms are null between different spins. For the restricted case which assumes closed-shell orbitals and single- determinantal wavefunctions, the Fock operator for the ''i''-th electron is given by:Levine, I.N. (1991) ''Quantum Chemistry'' (4th ed., Prentice-Hall), p.403 :\hat F(i) = \hat h(i)+\sum_^ \hat J_j(i)-\hat K_j(i)/math> where: :\hat F(i) is the Fock operator for the ''i''-th electron in the system, :(i) is the one-electron Hamiltonian Hamiltonian may refer to: * Hamiltonian mechanics, a function that represents the total energy of a system * Hamiltonian (quantum mechanics), an operator corresponding to the total ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Overlap Matrix
In chemical bonds, an orbital overlap is the concentration of orbitals on adjacent atoms in the same regions of space. Orbital overlap can lead to bond formation. The general principle for orbital overlap is that, the greater the overlap between orbitals, the greater the bond strength. Linus Pauling explained the importance of orbital overlap in the molecular bond angles observed through experimentation; it is the basis for orbital hybridization. As ''s'' orbitals are spherical (and have no directionality) and ''p'' orbitals are oriented 90° to each other, a theory was needed to explain why molecules such as methane (CH4) had observed bond angles of 109.5°. Pauling proposed that s and p orbitals on the carbon atom can combine to form hybrids (sp3 in the case of methane) which are directed toward the hydrogen atoms. The carbon hybrid orbitals have greater overlap with the hydrogen orbitals, and can therefore form stronger C–H bonds.Pauling, Linus. (1960). ''The Nature ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Wave Function
In quantum physics, a wave function (or wavefunction) is a mathematical description of the quantum state of an isolated quantum system. The most common symbols for a wave function are the Greek letters and (lower-case and capital psi (letter), psi, respectively). Wave functions are complex number, complex-valued. For example, a wave function might assign a complex number to each point in a region of space. The Born rule provides the means to turn these complex probability amplitudes into actual probabilities. In one common form, it says that the squared modulus of a wave function that depends upon position is the probability density function, probability density of measurement in quantum mechanics, measuring a particle as being at a given place. The integral of a wavefunction's squared modulus over all the system's degrees of freedom must be equal to 1, a condition called ''normalization''. Since the wave function is complex-valued, only its relative phase and relative magnitud ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Energy
Energy () is the physical quantity, quantitative physical property, property that is transferred to a physical body, body or to a physical system, recognizable in the performance of Work (thermodynamics), work and in the form of heat and light. Energy is a Conservation law, conserved quantity—the law of conservation of energy states that energy can be Energy transformation, converted in form, but not created or destroyed. The unit of measurement for energy in the International System of Units (SI) is the joule (J). Forms of energy include the kinetic energy of a moving object, the potential energy stored by an object (for instance due to its position in a Classical field theory, field), the elastic energy stored in a solid object, chemical energy associated with chemical reactions, the radiant energy carried by electromagnetic radiation, the internal energy contained within a thermodynamic system, and rest energy associated with an object's rest mass. These are not mutual ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Observable
In physics, an observable is a physical property or physical quantity that can be measured. In classical mechanics, an observable is a real-valued "function" on the set of all possible system states, e.g., position and momentum. In quantum mechanics, an observable is an operator, or gauge, where the property of the quantum state can be determined by some sequence of operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value. Physically meaningful observables must also satisfy transformation laws that relate observations performed by different observers in different frames of reference. These transformation laws are automorphisms of the state space, that is bijective transformations that preserve certain mathematical properties of the space in question. Quantum mechanics In quantum mechanics, observables manifest as self-adjoint operators on a separable complex Hilbert space ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Unrestricted Hartree–Fock
Unrestricted Hartree–Fock (UHF) theory is the most common molecular orbital method for open shell molecules where the number of electrons of each spin are not equal. While restricted Hartree–Fock theory uses a single molecular orbital twice, one multiplied by the α spin function and the other multiplied by the β spin function in the Slater determinant, unrestricted Hartree–Fock theory uses different molecular orbitals for the α and β electrons. This has been called a ''different orbitals for different spins'' (DODS) method. The result is a pair of coupled Roothaan equations, known as the Pople–Nesbet–Berthier equations. :\mathbf^\alpha\ \mathbf^\alpha\ = \mathbf \mathbf^\alpha\ \mathbf^\alpha\ :\mathbf^\beta\ \mathbf^\beta\ = \mathbf \mathbf^\beta\ \mathbf^\beta\ Where \mathbf^\alpha\ and \mathbf^\beta\ are the Fock matrices for the \alpha\ and \beta\ orbitals, \mathbf^\alpha\ and \mathbf^\beta\ are the matrices of coefficients for the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |