|
Radius Of Gyration
''Radius of gyration'' or gyradius of a body about the axis of rotation is defined as the radial distance to a point which would have a moment of inertia the same as the body's actual distribution of mass, if the total mass of the body were concentrated there. Mathematically the radius of gyration is the root mean square distance of the object's parts from either its center of mass or a given axis, depending on the relevant application. It is actually the perpendicular distance from point mass to the axis of rotation. One can represent a trajectory of a moving point as a body. Then radius of gyration can be used to characterize the typical distance travelled by this point. Suppose a body consists of n particles each of mass m. Let r_1, r_2, r_3, \dots , r_n be their perpendicular distances from the axis of rotation. Then, the moment of inertia I of the body about the axis of rotation is :I = m_1 r_1^2 + m_2 r_2^2 + \cdots + m_n r_n^2 : If all the masses are the same (m), then ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Axis Of Rotation
Rotation around a fixed axis is a special case of rotational motion. The fixed-axis hypothesis excludes the possibility of an axis changing its orientation and cannot describe such phenomena as wobbling or precession. According to Euler's rotation theorem, simultaneous rotation along a number of stationary axes at the same time is impossible; if two rotations are forced at the same time, a new axis of rotation will appear. This article assumes that the rotation is also stable, such that no torque is required to keep it going. The kinematics and dynamics of rotation around a fixed axis of a rigid body are mathematically much simpler than those for free rotation of a rigid body; they are entirely analogous to those of linear motion along a single fixed direction, which is not true for ''free rotation of a rigid body''. The expressions for the kinetic energy of the object, and for the forces on the parts of the object, are also simpler for rotation around a fixed axis, than for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tensor
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects related to a vector space. Tensors may map between different objects such as vectors, scalars, and even other tensors. There are many types of tensors, including scalars and vectors (which are the simplest tensors), dual vectors, multilinear maps between vector spaces, and even some operations such as the dot product. Tensors are defined independent of any basis, although they are often referred to by their components in a basis related to a particular coordinate system. Tensors have become important in physics because they provide a concise mathematical framework for formulating and solving physics problems in areas such as mechanics (stress, elasticity, fluid mechanics, moment of inertia, ...), electrodynamics (electromagnetic tensor, Maxwell tensor, permittivity, magnetic susceptibility, ...), general relativity ( stress–energy tensor, cur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamic Light Scattering
Dynamic light scattering (DLS) is a technique in physics that can be used to determine the size distribution profile of small particles in suspension or polymers in solution. In the scope of DLS, temporal fluctuations are usually analyzed using the intensity or photon auto-correlation function (also known as photon correlation spectroscopy or quasi-elastic light scattering). In the time domain analysis, the autocorrelation function (ACF) usually decays starting from zero delay time, and faster dynamics due to smaller particles lead to faster decorrelation of scattered intensity trace. It has been shown that the intensity ACF is the Fourier transform of the power spectrum, and therefore the DLS measurements can be equally well performed in the spectral domain. DLS can also be used to probe the behavior of complex fluids such as concentrated polymer solutions. Setup A monochromatic light source, usually a laser, is shot through a polarizer and into a sample. The scattered light then ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hydrodynamic Radius
The hydrodynamic radius of a macromolecule or colloid particle is R_. The macromolecule or colloid particle is a collection of N subparticles. This is done most commonly for polymers; the subparticles would then be the units of the polymer. R_ is defined by : \frac \ \stackrel\ \frac \left\langle \sum_ \frac \right\rangle where r_ is the distance between subparticles i and j, and where the angular brackets \langle \ldots \rangle represent an ensemble average. The theoretical hydrodynamic radius R_ was originally an estimate by John Gamble Kirkwood of the Stokes radius of a polymer, and some sources still use ''hydrodynamic radius'' as a synonym for the Stokes radius. Note that in biophysics, hydrodynamic radius refers to the Stokes radius, or commonly to the apparent Stokes radius obtained from size exclusion chromatography. The theoretical hydrodynamic radius R_ arises in the study of the dynamic properties of polymers moving in a solvent. It is often similar in magnitu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Small-angle X-ray Scattering
Small-angle X-ray scattering (SAXS) is a small-angle scattering technique by which nanoscale density differences in a sample can be quantified. This means that it can determine nanoparticle size distributions, resolve the size and shape of (monodisperse) macromolecules, determine pore sizes, characteristic distances of partially ordered materials, and much more. This is achieved by analyzing the elastic scattering behaviour of X-rays when travelling through the material, recording their scattering at small angles (typically 0.1 – 10°, hence the "Small-angle" in its name). It belongs to the family of small-angle scattering (SAS) techniques along with small-angle neutron scattering, and is typically done using hard X-rays with a wavelength of 0.07 – 0.2 nm.. Depending on the angular range in which a clear scattering signal can be recorded, SAXS is capable of delivering structural information of dimensions between 1 and 100 nm, and of repeat distances in partially ordered s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Small-angle Neutron Scattering
Small-angle neutron scattering (SANS) is an experimental technique that uses elastic neutron scattering at small scattering angles to investigate the structure of various substances at a mesoscopic scale of about 1–100 nm. Small angle neutron scattering is in many respects very similar to small-angle X-ray scattering (SAXS); both techniques are jointly referred to as small-angle scattering (SAS). Advantages of SANS over SAXS are its sensitivity to light elements, the possibility of isotope labelling, and the strong scattering by magnetic moments. Technique During a SANS experiment a beam of neutrons is directed at a sample, which can be an aqueous solution, a solid, a powder, or a crystal. The neutrons are elastically scattered by nuclear interaction with the nuclei or interaction with magnetic momentum of unpaired electrons. In X-ray scattering, photons interact with the electronic cloud so the bigger the element, the bigger the effect is. In neutron scattering, neutron ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Static Light Scattering
Static light scattering is a technique in physical chemistry that measures the intensity of the scattered light to obtain the average molecular weight ''Mw'' of a macromolecule like a polymer or a protein in solution. Measurement of the scattering intensity at many angles allows calculation of the root mean square radius, also called the radius of gyration ''Rg''. By measuring the scattering intensity for many samples of various concentrations, the second virial coefficient, ''A2'', can be calculated. Static light scattering is also commonly utilized to determine the size of particle suspensions in the sub-μm and supra-μm ranges, via the Lorenz-Mie (see Mie scattering) and Fraunhofer diffraction formalisms, respectively. For static light scattering experiments, a high-intensity monochromatic light, usually a laser, is launched into a solution containing the macromolecules. One or many detectors are used to measure the scattering intensity at one or many angles. The angular depend ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Contour Length
Contour length is a term used in molecular physics. The contour length of a polymer chain (a big molecule consisting of many similar smaller molecules) is its length at maximum physically possible extension Extension, extend or extended may refer to: Mathematics Logic or set theory * Axiom of extensionality * Extensible cardinal * Extension (model theory) * Extension (predicate logic), the set of tuples of values that satisfy the predicate * E .... 2nd Edition, 1997 Contour length is equal to the product of the number of segments of polymer molecule(n) and its length(l). References [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ensemble Average
In physics, specifically statistical mechanics, an ensemble (also statistical ensemble) is an idealization consisting of a large number of virtual copies (sometimes infinitely many) of a system, considered all at once, each of which represents a possible state that the real system might be in. In other words, a statistical ensemble is a set of systems of particles used in statistical mechanics to describe a single system. The concept of an ensemble was introduced by J. Willard Gibbs in 1902. A thermodynamic ensemble is a specific variety of statistical ensemble that, among other properties, is in statistical equilibrium (defined below), and is used to derive the properties of thermodynamic systems from the laws of classical or quantum mechanics. Physical considerations The ensemble formalises the notion that an experimenter repeating an experiment again and again under the same macroscopic conditions, but unable to control the microscopic details, may expect to observe a rang ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ensemble Average
In physics, specifically statistical mechanics, an ensemble (also statistical ensemble) is an idealization consisting of a large number of virtual copies (sometimes infinitely many) of a system, considered all at once, each of which represents a possible state that the real system might be in. In other words, a statistical ensemble is a set of systems of particles used in statistical mechanics to describe a single system. The concept of an ensemble was introduced by J. Willard Gibbs in 1902. A thermodynamic ensemble is a specific variety of statistical ensemble that, among other properties, is in statistical equilibrium (defined below), and is used to derive the properties of thermodynamic systems from the laws of classical or quantum mechanics. Physical considerations The ensemble formalises the notion that an experimenter repeating an experiment again and again under the same macroscopic conditions, but unable to control the microscopic details, may expect to observe a rang ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
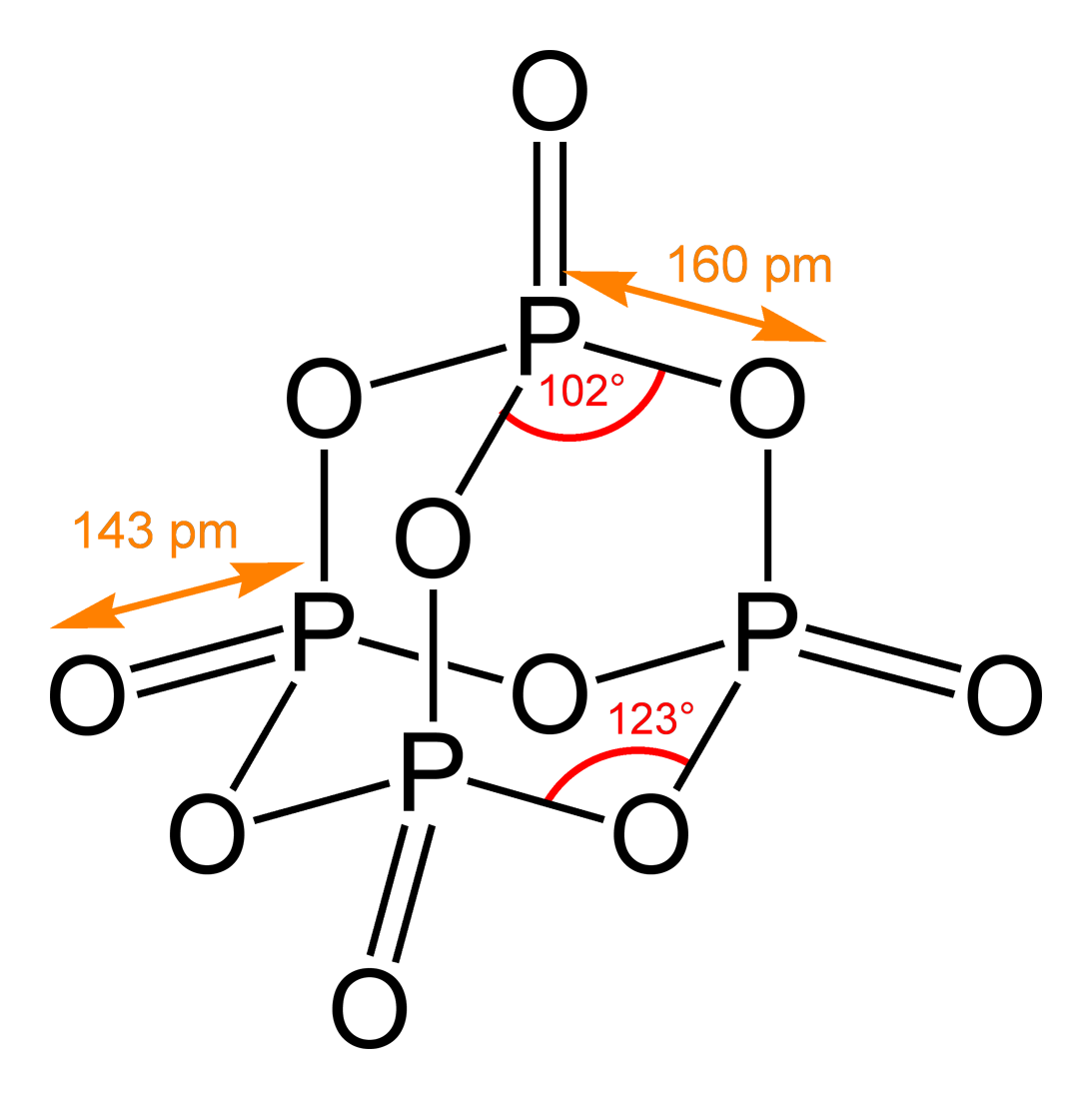
Chemical Structure
A chemical structure determination includes a chemist's specifying the molecular geometry and, when feasible and necessary, the electronic structure of the target molecule or other solid. Molecular geometry refers to the spatial arrangement of atoms in a molecule and the chemical bonds that hold the atoms together, and can be represented using structural formulae and by molecular models; complete electronic structure descriptions include specifying the occupation of a molecule's molecular orbitals. Structure determination can be applied to a range of targets from very simple molecules (e.g., diatomic oxygen or nitrogen), to very complex ones (e.g., such as protein or DNA). Background Theories of chemical structure were first developed by August Kekulé, Archibald Scott Couper, and Aleksandr Butlerov, among others, from about 1858. These theories were first to state that chemical compounds are not a random cluster of atoms and functional groups, but rather had a definite order ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean
There are several kinds of mean in mathematics, especially in statistics. Each mean serves to summarize a given group of data, often to better understand the overall value (magnitude and sign) of a given data set. For a data set, the ''arithmetic mean'', also known as "arithmetic average", is a measure of central tendency of a finite set of numbers: specifically, the sum of the values divided by the number of values. The arithmetic mean of a set of numbers ''x''1, ''x''2, ..., x''n'' is typically denoted using an overhead bar, \bar. If the data set were based on a series of observations obtained by sampling from a statistical population, the arithmetic mean is the ''sample mean'' (\bar) to distinguish it from the mean, or expected value, of the underlying distribution, the ''population mean'' (denoted \mu or \mu_x).Underhill, L.G.; Bradfield d. (1998) ''Introstat'', Juta and Company Ltd.p. 181/ref> Outside probability and statistics, a wide range of other notions of mean are o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |