|
Rotating Wave Approximation
The rotating-wave approximation is an approximation used in atom optics and magnetic resonance. In this approximation, terms in a Hamiltonian that oscillate rapidly are neglected. This is a valid approximation when the applied electromagnetic radiation is near resonance with an atomic transition, and the intensity is low. Explicitly, terms in the Hamiltonians that oscillate with frequencies \omega_L + \omega_0 are neglected, while terms that oscillate with frequencies \omega_L - \omega_0 are kept, where \omega_L is the light frequency, and \omega_0 is a transition frequency. The name of the approximation stems from the form of the Hamiltonian in the interaction picture, as shown below. By switching to this picture the evolution of an atom due to the corresponding atomic Hamiltonian is absorbed into the system ket, leaving only the evolution due to the interaction of the atom with the light field to consider. It is in this picture that the rapidly oscillating terms mentioned previ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Atom Optics
Atom optics (or atomic optics) is the area of physics which deals with beams of cold, slowly moving neutral atoms, as a special case of a particle beam. Like an optical beam, the atomic beam may exhibit diffraction and interference, and can be focused with a Fresnel zone plate or a concave atomic mirror. Several scientific groups work in this field.Atom Optics at the University of Queensland (Australia) homepage Until 2006, the resolution of imaging systems based on atomic beams was not better than that of an optical microscope, mainly due to the poor performance of the focusing elements. Such elements use small numerical aperture; usually, atomic mirrors use grazing incidence, and the reflectivity drops drastically with increase of the grazing angle; for efficient normal reflection, atoms should be ultracold, and dealing with such atoms usually involves magnetic, magneto-optical or optical traps. Recent scientific publications about Atom Nano-Optics, evanescent field lenses ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transition Dipole Moment
The transition dipole moment or transition moment, usually denoted \mathbf_ for a transition between an initial state, m, and a final state, n, is the electric dipole moment associated with the transition between the two states. In general the transition dipole moment is a complex vector quantity that includes the phase factors associated with the two states. Its direction gives the polarization of the transition, which determines how the system will interact with an electromagnetic wave of a given polarization, while the square of the magnitude gives the strength of the interaction due to the distribution of charge within the system. The SI unit of the transition dipole moment is the Coulomb-meter (Cm); a more conveniently sized unit is the Debye (D). Definition A single charged particle For a transition where a single charged particle changes state from , \psi_a \rangle to , \psi_b \rangle , the transition dipole moment \text is (\text a \rightarrow b) = \langle \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor Series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor series are named after Brook Taylor, who introduced them in 1715. A Taylor series is also called a Maclaurin series, when 0 is the point where the derivatives are considered, after Colin Maclaurin, who made extensive use of this special case of Taylor series in the mid-18th century. The partial sum formed by the first terms of a Taylor series is a polynomial of degree that is called the th Taylor polynomial of the function. Taylor polynomials are approximations of a function, which become generally better as increases. Taylor's theorem gives quantitative estimates on the error introduced by the use of such approximations. If the Taylor series of a function is convergent, its sum is the limit of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schrödinger Picture
In physics, the Schrödinger picture is a formulation of quantum mechanics in which the state vectors evolve in time, but the operators (observables and others) are mostly constant with respect to time (an exception is the Hamiltonian which may change if the potential V changes). This differs from the Heisenberg picture which keeps the states constant while the observables evolve in time, and from the interaction picture in which both the states and the observables evolve in time. The Schrödinger and Heisenberg pictures are related as active and passive transformations and commutation relations between operators are preserved in the passage between the two pictures. In the Schrödinger picture, the state of a system evolves with time. The evolution for a closed quantum system is brought about by a unitary operator, the time evolution operator. For time evolution from a state vector , \psi(t_0)\rangle at time 0 to a state vector , \psi(t)\rangle at time , the time-evolution ope ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
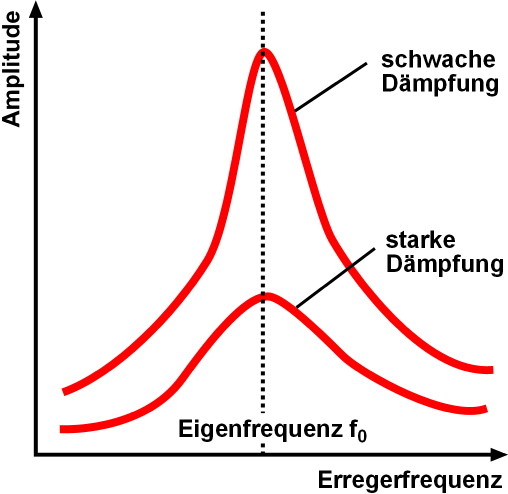
Resonance
Resonance describes the phenomenon of increased amplitude that occurs when the frequency of an applied periodic force (or a Fourier component of it) is equal or close to a natural frequency of the system on which it acts. When an oscillating force is applied at a resonant frequency of a dynamic system, the system will oscillate at a higher amplitude than when the same force is applied at other, non-resonant frequencies. Frequencies at which the response amplitude is a relative maximum are also known as resonant frequencies or resonance frequencies of the system. Small periodic forces that are near a resonant frequency of the system have the ability to produce large amplitude oscillations in the system due to the storage of vibrational energy. Resonance phenomena occur with all types of vibrations or waves: there is mechanical resonance, orbital resonance, acoustic resonance, electromagnetic resonance, nuclear magnetic resonance (NMR), electron spin resonance (ESR) a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unitary Transformation
In mathematics, a unitary transformation is a transformation that preserves the inner product: the inner product of two vectors before the transformation is equal to their inner product after the transformation. Formal definition More precisely, a unitary transformation is an isomorphism between two inner product spaces (such as Hilbert spaces). In other words, a ''unitary transformation'' is a bijective function U : H \to H_2\, between two inner product spaces, H and H_2, such that \langle Ux, Uy \rangle_ = \langle x, y \rangle_ \quad \text x, y \in H. Properties A unitary transformation is an isometry, as one can see by setting x=y in this formula. Unitary operator In the case when H_1 and H_2 are the same space, a unitary transformation is an automorphism of that Hilbert space, and then it is also called a unitary operator. Antiunitary transformation A closely related notion is that of antiunitary transformation, which is a bijective function :U:H_1\to H_2\, between t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
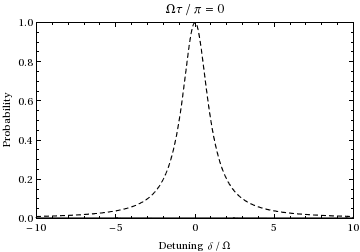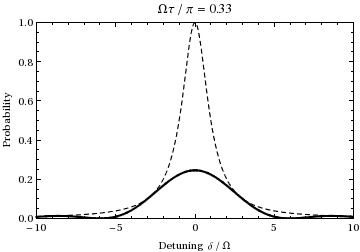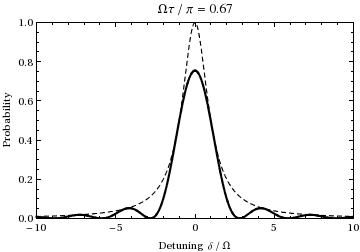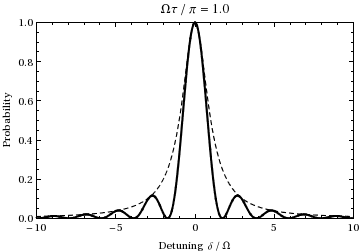
Rabi Frequency
The Rabi frequency is the frequency at which the probability amplitudes of two atomic energy levels fluctuate in an oscillating electromagnetic field. It is proportional to the Transition Dipole Moment of the two levels and to the amplitude (''not'' intensity) of the Electromagnetic field. Population transfer between the levels of such a 2-level system illuminated with light exactly resonant with the difference in energy between the two levels will occur at the Rabi frequency; when the incident light is detuned from this energy difference (detuned from resonance) then the population transfer occurs at the generalized Rabi frequency. The Rabi frequency is a semiclassical concept since it treats the atom as an object with quantized energy levels and the electromagnetic field as a continuous wave. In the context of a nuclear magnetic resonance experiment, the Rabi frequency is the nutation frequency of a sample's net nuclear magnetization vector about a radio-frequency field. (Not ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivation
Derivation may refer to: Language * Morphological derivation, a word-formation process * Parse tree or concrete syntax tree, representing a string's syntax in formal grammars Law * Derivative work, in copyright law * Derivation proceeding, a proceeding in United States patent law Music * The creation of a derived row, in the twelve-tone musical technique Science and mathematics * Derivation (differential algebra), a unary function satisfying the Leibniz product law * Formal proof or derivation, a sequence of sentences each of which is an axiom or follows from the preceding sentences in the sequence by a rule of inference * An after-the-fact justification for an action, in the work of sociologist Vilfredo Pareto See also *Derive (other), for meanings of "derive" and "derived" *Derivative In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Conjugate
In mathematics, the complex conjugate of a complex number is the number with an equal real part and an imaginary part equal in magnitude but opposite in sign. That is, (if a and b are real, then) the complex conjugate of a + bi is equal to a - bi. The complex conjugate of z is often denoted as \overline or z^*. In polar form, the conjugate of r e^ is r e^. This can be shown using Euler's formula. The product of a complex number and its conjugate is a real number: a^2 + b^2 (or r^2 in polar coordinates). If a root of a univariate polynomial with real coefficients is complex, then its complex conjugate is also a root. Notation The complex conjugate of a complex number z is written as \overline z or z^*. The first notation, a vinculum, avoids confusion with the notation for the conjugate transpose of a matrix, which can be thought of as a generalization of the complex conjugate. The second is preferred in physics, where dagger (†) is used for the conju ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Energy Eigenstate
A stationary state is a quantum state with all observables independent of time. It is an eigenvector of the energy operator (instead of a quantum superposition of different energies). It is also called energy eigenvector, energy eigenstate, energy eigenfunction, or energy eigenket. It is very similar to the concept of atomic orbital and molecular orbital in chemistry, with some slight differences explained below. Introduction A stationary state is called ''stationary'' because the system remains in the same state as time elapses, in every observable way. For a single-particle Hamiltonian, this means that the particle has a constant probability distribution for its position, its velocity, its spin, etc. (This is true assuming the particle's environment is also static, i.e. the Hamiltonian is unchanging in time.) The wavefunction itself is not stationary: It continually changes its overall complex phase factor, so as to form a standing wave. The oscillation frequency of the sta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dipole
In physics, a dipole () is an electromagnetic phenomenon which occurs in two ways: *An electric dipole deals with the separation of the positive and negative electric charges found in any electromagnetic system. A simple example of this system is a pair of charges of equal magnitude but opposite sign separated by some typically small distance. (A permanent electric dipole is called an electret.) *A magnetic dipole is the closed circulation of an electric current system. A simple example is a single loop of wire with constant current through it. A bar magnet is an example of a magnet with a permanent magnetic dipole moment. Dipoles, whether electric or magnetic, can be characterized by their dipole moment, a vector quantity. For the simple electric dipole, the electric dipole moment points from the negative charge towards the positive charge, and has a magnitude equal to the strength of each charge times the separation between the charges. (To be precise: for the definition ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |