|
Rhombi
In plane Euclidean geometry, a rhombus (plural rhombi or rhombuses) is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. The rhombus is often called a "diamond", after the diamonds suit in playing cards which resembles the projection of an octahedral diamond, or a lozenge, though the former sometimes refers specifically to a rhombus with a 60° angle (which some authors call a calisson after the French sweet – also see Polyiamond), and the latter sometimes refers specifically to a rhombus with a 45° angle. Every rhombus is simple (non-self-intersecting), and is a special case of a parallelogram and a kite. A rhombus with right angles is a square. Etymology The word "rhombus" comes from grc, ῥόμβος, rhombos, meaning something that spins, which derives from the verb , romanized: , meaning "to turn round and round." The word was used both by Eucli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kite (geometry)
In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word ''deltoid'' may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals.See H. S. M. Coxeter's review of in : "It is unfortunate that the author uses, instead of 'kite', the name 'deltoid', which belongs more properly to a curve, the three-cusped hypocycloid." A kite may also be called a dart, particularly if it is not convex. Every kite is an orthodiagonal quadrilateral (its diagonals are at right angles) and, when convex, a tangential quadrilateral (its sides are tangent to an inscribed circle). The convex kites are exactly the quadrilaterals that are both orthodiagonal and tangential. They include as special cases the right kites, with two opposite right angles; the rhombi, with two ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kite (geometry)
In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word ''deltoid'' may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals.See H. S. M. Coxeter's review of in : "It is unfortunate that the author uses, instead of 'kite', the name 'deltoid', which belongs more properly to a curve, the three-cusped hypocycloid." A kite may also be called a dart, particularly if it is not convex. Every kite is an orthodiagonal quadrilateral (its diagonals are at right angles) and, when convex, a tangential quadrilateral (its sides are tangent to an inscribed circle). The convex kites are exactly the quadrilaterals that are both orthodiagonal and tangential. They include as special cases the right kites, with two opposite right angles; the rhombi, with two ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Octahedron
In geometry, an octahedron (plural: octahedra, octahedrons) is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. A regular octahedron is the dual polyhedron of a cube. It is a rectified tetrahedron. It is a square bipyramid in any of three orthogonal orientations. It is also a triangular antiprism in any of four orientations. An octahedron is the three-dimensional case of the more general concept of a cross polytope. A regular octahedron is a 3-ball in the Manhattan () metric. Regular octahedron Dimensions If the edge length of a regular octahedron is ''a'', the radius of a circumscribed sphere (one that touches the octahedron at all vertices) is :r_u = \frac a \approx 0.707 \cdot a and the radius of an inscribed sphere (tangent to each of the octahedron's faces) is :r_i = \frac a \approx 0.408\cdot a while the midradius, which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isotoxal Figure
In geometry, a polytope (for example, a polygon or a polyhedron) or a tiling is isotoxal () or edge-transitive if its symmetries act transitively on its edges. Informally, this means that there is only one type of edge to the object: given two edges, there is a translation, rotation, and/or reflection that will move one edge to the other, while leaving the region occupied by the object unchanged. Isotoxal polygons An isotoxal polygon is an even-sided i.e. equilateral polygon, but not all equilateral polygons are isotoxal. The duals of isotoxal polygons are isogonal polygons. Isotoxal 4n-gons are centrally symmetric, so are also zonogons. In general, an isotoxal 2n-gon has \mathrm_n, (^*nn) dihedral symmetry. For example, a rhombus is an isotoxal "2×2-gon" (quadrilateral) with \mathrm_2, (^*22) symmetry. All regular polygons (equilateral triangle, square, etc.) are isotoxal, having double the minimum symmetry order: a regular n-gon has \mathrm_n, (^*nn) dihedral symmetry. An ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polyiamond
A polyiamond (also polyamond or simply iamond, or sometimes triangular polyomino) is a polyform whose base form is an equilateral triangle. The word ''polyiamond'' is a back-formation from ''diamond'', because this word is often used to describe the shape of a pair of equilateral triangles placed base to base, and the initial 'di-' looks like a Greek prefix meaning 'two-' (though ''diamond'' actually derives from Greek '' ἀδάμας'' - also the basis for the word "adamant"). The name was suggested by recreational mathematics writer Thomas H. O'Beirne in ''New Scientist'' 1961 number 1, page 164. Counting The basic combinatorial question is, How many different polyiamonds exist with a given number of cells? Like polyominoes, polyiamonds may be either free or one-sided. Free polyiamonds are invariant under reflection as well as translation and rotation. One-sided polyiamonds distinguish reflections. The number of free ''n''-iamonds for ''n'' = 1, 2, 3, ... is: :1, 1, 1, 3, 4, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archimedes
Archimedes of Syracuse (;; ) was a Greek mathematician, physicist, engineer, astronomer, and inventor from the ancient city of Syracuse in Sicily. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Considered the greatest mathematician of ancient history, and one of the greatest of all time,* * * * * * * * * * Archimedes anticipated modern calculus and analysis by applying the concept of the infinitely small and the method of exhaustion to derive and rigorously prove a range of geometrical theorems. These include the area of a circle, the surface area and volume of a sphere, the area of an ellipse, the area under a parabola, the volume of a segment of a paraboloid of revolution, the volume of a segment of a hyperboloid of revolution, and the area of a spiral. Heath, Thomas L. 1897. ''Works of Archimedes''. Archimedes' other mathematical achievements include deriving an approximation of pi, defining and in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square
In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length adjacent sides. It is the only regular polygon whose internal angle, central angle, and external angle are all equal (90°), and whose diagonals are all equal in length. A square with vertices ''ABCD'' would be denoted . Characterizations A convex quadrilateral is a square if and only if it is any one of the following: * A rectangle with two adjacent equal sides * A rhombus with a right vertex angle * A rhombus with all angles equal * A parallelogram with one right vertex angle and two adjacent equal sides * A quadrilateral with four equal sides and four right angles * A quadrilateral where the diagonals are equal, and are the perpendicular bisectors of each other (i.e., a rhombus with equal diagonals) * A convex quadrilateral with successiv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclid
Euclid (; grc-gre, Wikt:Εὐκλείδης, Εὐκλείδης; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the ''Euclid's Elements, Elements'' treatise, which established the foundations of geometry that largely dominated the field until the early 19th century. His system, now referred to as Euclidean geometry, involved new innovations in combination with a synthesis of theories from earlier Greek mathematicians, including Eudoxus of Cnidus, Hippocrates of Chios, Thales and Theaetetus (mathematician), Theaetetus. With Archimedes and Apollonius of Perga, Euclid is generally considered among the greatest mathematicians of antiquity, and one of the most influential in the history of mathematics. Very little is known of Euclid's life, and most information comes from the philosophers Proclus and Pappus of Alexandria many centuries later. Until the early Renaissance he was often mistaken f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
For The Learning Of Mathematics
''For the Learning of Mathematics'' is a triannual peer-reviewed academic journal covering mathematics education. It was established in 1981 by David Wheeler. Abstracting and indexing The journal is abstracted and indexed in: * EBSCO databases *Education Resources Information Center *Index Islamicus * ProQuest databases *Scopus Reception In 2012, a survey of researchers in the field ranked the journal with an A (the second highest ranking, below A*). In 2017, another ranking of journals placed it in the top tier. At the same time, the high ranking in both of these reviews was questioned, suggesting that the journal more properly belongs in the mid-tier. Editors-in-chief The following persons are or have been editor-in-chief: *David Wheeler (1981–1996) *David Pimm (1997–2002) *Laurinda Brown (2003–2007) *Brent Davis (2008–2010) *Richard Barwell (2011–2016) *David Reid (2017–present) See also * List of mathematics education journals This is a list of notable academic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadrilateral
In geometry a quadrilateral is a four-sided polygon, having four edges (sides) and four corners (vertices). The word is derived from the Latin words ''quadri'', a variant of four, and ''latus'', meaning "side". It is also called a tetragon, derived from greek "tetra" meaning "four" and "gon" meaning "corner" or "angle", in analogy to other polygons (e.g. pentagon). Since "gon" means "angle", it is analogously called a quadrangle, or 4-angle. A quadrilateral with vertices A, B, C and D is sometimes denoted as \square ABCD. Quadrilaterals are either simple (not self-intersecting), or complex (self-intersecting, or crossed). Simple quadrilaterals are either convex or concave. The interior angles of a simple (and planar) quadrilateral ''ABCD'' add up to 360 degrees of arc, that is :\angle A+\angle B+\angle C+\angle D=360^. This is a special case of the ''n''-gon interior angle sum formula: ''S'' = (''n'' − 2) × 180°. All non-self-crossing quadrilaterals tile the plane, b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bicone
In geometry, a bicone or dicone (from la, bi-, and Greek: ''di-'', both meaning "two") is the three-dimensional surface of revolution of a rhombus around one of its axes of symmetry. Equivalently, a bicone is the surface created by joining two congruent, right, circular cones at their bases. A bicone has circular symmetry and orthogonal bilateral symmetry. Geometry For a circular bicone with radius ''R'' and height center-to-top ''H'', the formula for volume becomes :V = \frac \pi R^2 H. For a right circular cone, the surface area is :SA =2\pi R S\, where S = \sqrt is the slant height. See also * Sphericon * Biconical antenna In radio systems, a biconical antenna is a broad-bandwidth antenna made of two roughly conical conductive objects, nearly touching at their points.Zhuohui Zhang,''Analysis and design of a broadband antenna for software defined radio'', ProQuest, 2 ... References External links * Elementary geometry Surfaces {{ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
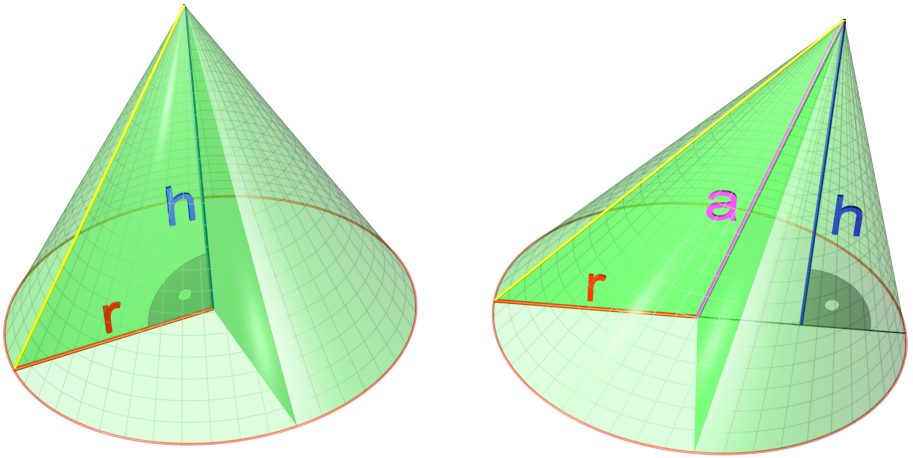
Cone
A cone is a three-dimensional geometric shape that tapers smoothly from a flat base (frequently, though not necessarily, circular) to a point called the apex or vertex. A cone is formed by a set of line segments, half-lines, or lines connecting a common point, the apex, to all of the points on a base that is in a plane that does not contain the apex. Depending on the author, the base may be restricted to be a circle, any one-dimensional quadratic form in the plane, any closed one-dimensional figure, or any of the above plus all the enclosed points. If the enclosed points are included in the base, the cone is a solid object; otherwise it is a two-dimensional object in three-dimensional space. In the case of a solid object, the boundary formed by these lines or partial lines is called the ''lateral surface''; if the lateral surface is unbounded, it is a conical surface. In the case of line segments, the cone does not extend beyond the base, while in the case of half-lin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
_by_Thomas_Degeorge.png)