|
Quantum Capacitance
Quantum capacitance, also called chemical capacitance and electrochemical capacitance C_\bar, is a quantity first introduced by Serge Luryi (1988), and is defined as the variation of electrical charge q with respect to the variation of electrochemical potential \bar, i.e., C_ = \frac. In the simplest example, if you make a parallel-plate capacitor where one or both of the plates has a low density of states, then the capacitance is ''not'' given by the normal formula for parallel-plate capacitors, C_e. Instead, the capacitance is lower, as if there was another capacitor in series, C_q. This second capacitance, related to the density of states of the plates, is the quantum capacitance and is represented by C_q. The equivalent capacitance is called electrochemical capacitance \frac = \frac + \frac. Quantum capacitance is especially important for low-density-of-states systems, such as a 2-dimensional electronic system in a semiconductor surface or interface or graphene, and can be use ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electric Charge
Electric charge is the physical property of matter that causes charged matter to experience a force when placed in an electromagnetic field. Electric charge can be ''positive'' or ''negative'' (commonly carried by protons and electrons respectively). Like charges repel each other and unlike charges attract each other. An object with an absence of net charge is referred to as neutral. Early knowledge of how charged substances interact is now called classical electrodynamics, and is still accurate for problems that do not require consideration of quantum effects. Electric charge is a conserved property; the net charge of an isolated system, the amount of positive charge minus the amount of negative charge, cannot change. Electric charge is carried by subatomic particles. In ordinary matter, negative charge is carried by electrons, and positive charge is carried by the protons in the nuclei of atoms. If there are more electrons than protons in a piece of matter, it will have ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
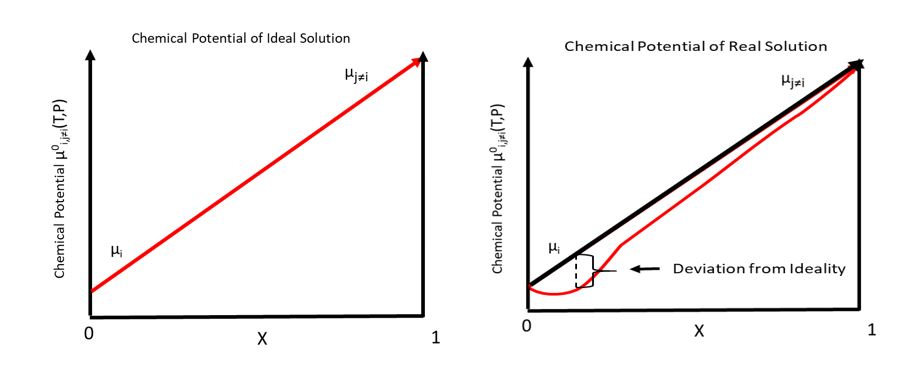
Chemical Potential
In thermodynamics, the chemical potential of a species is the energy that can be absorbed or released due to a change of the particle number of the given species, e.g. in a chemical reaction or phase transition. The chemical potential of a species in a mixture is defined as the rate of change of free energy of a thermodynamic system with respect to the change in the number of atoms or molecules of the species that are added to the system. Thus, it is the partial derivative of the free energy with respect to the amount of the species, all other species' concentrations in the mixture remaining constant. When both temperature and pressure are held constant, and the number of particles is expressed in moles, the chemical potential is the partial molar Gibbs free energy. At chemical equilibrium or in phase equilibrium, the total sum of the product of chemical potentials and stoichiometric coefficients is zero, as the free energy is at a minimum. In a system in diffusion equilibrium, th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Supercapacitor
A supercapacitor (SC), also called an ultracapacitor, is a high-capacity capacitor, with a capacitance value much higher than other capacitors but with lower voltage limits. It bridges the gap between electrolytic capacitors and rechargeable batteries. It typically stores 10 to 100 times more energy per unit volume or mass than electrolytic capacitors, can accept and deliver charge much faster than batteries, and tolerates many more charge and discharge cycles than rechargeable batteries. Supercapacitors are used in applications requiring many rapid charge/discharge cycles, rather than long-term compact energy storage — in automobiles, buses, trains, cranes and elevators, where they are used for regenerative braking, short-term energy storage, or burst-mode power delivery. Smaller units are used as power backup for static random-access memory (SRAM). Unlike ordinary capacitors, supercapacitors do not use the conventional solid dielectric, but rather, they use electrosta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Capacitance–voltage Profiling
Capacitance–voltage profiling (or C–V profiling, sometimes CV profiling) is a technique for characterizing semiconductor materials and devices. The applied voltage is varied, and the capacitance is measured and plotted as a function of voltage. The technique uses a metal–semiconductor junction (Schottky barrier) or a p–n junctionJ. Hilibrand and R.D. Gold, "Determination of the Impurity Distribution in Junction Diodes From Capacitance-Voltage Measurements", RCA Review, vol. 21, p. 245, June 1960 or a MOSFET to create a depletion region, a region which is empty of conducting electrons and holes, but may contain ionized donors and electrically active defects or ''traps''. The depletion region with its ionized charges inside behaves like a capacitor. By varying the voltage applied to the junction it is possible to vary the depletion width. The dependence of the depletion width upon the applied voltage provides information on the semiconductor's internal characteristics, such ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Juan Bisquert
Juan Bisquert (Düsseldorf, 1962), is a Spanish physicist known for his contributions to materials and devices for sustainable energy production. He grew up in Dénia, and he is a professor at Jaume I University in Castellón de la Plana. His work on solar cells relates physical principles and modelling of electronic and ionic processes to the interpretation of measurement techniques for the photovoltaic operation. Research activity At Universitat Jaume I he is the funding director of INAM (Institute of Advanced Materials), that develops research on materials, nanostructures and devices for the production of clean energy. He has published more than 400 papers in scientific journals. He has been cited more than 40,000 times in scientific journals. From 2014 to 2022 he appeared in the list " ISI Highly Cited Researchers" He wrote a series of books that have been published in the single volume "The Physics of Solar Energy Conversion". He edited the monography Photoelectrochemi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
TiO2
Titanium dioxide, also known as titanium(IV) oxide or titania , is the inorganic compound with the chemical formula . When used as a pigment, it is called titanium white, Pigment White 6 (PW6), or Colour Index International, CI 77891. It is a white solid that is insoluble to water, although mineral forms can appear black. As a pigment, it has a wide range of applications, including paint, sunscreen, and food coloring. When used as a food coloring, it has E number E171. World production in 2014 exceeded 9 million tonnes. It has been estimated that titanium dioxide is used in two-thirds of all pigments, and pigments based on the oxide have been valued at a price of $13.2 billion. Structure In all three of its main dioxides, titanium exhibits octahedral geometry, being bonded to six oxide anions. The oxides in turn are bonded to three Ti centers. The overall crystal structure of rutile is tetragonal in symmetry whereas anatase and brookite are orthorhombic. The oxygen substructu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dye-sensitized Solar Cells
A dye-sensitized solar cell (DSSC, DSC, DYSC or Grätzel cell) is a low-cost solar cell belonging to the group of thin film solar cells. It is based on a semiconductor formed between a photo-sensitized anode and an electrolyte, a '' photoelectrochemical'' system. The modern version of a dye solar cell, also known as the Grätzel cell, was originally co-invented in 1988 by Brian O'Regan and Michael Grätzel at UC Berkeley and this work was later developed by the aforementioned scientists at the École Polytechnique Fédérale de Lausanne (EPFL) until the publication of the first high efficiency DSSC in 1991. Michael Grätzel has been awarded the 2010 Millennium Technology Prize for this invention. The DSSC has a number of attractive features; it is simple to make using conventional roll-printing techniques, is semi-flexible and semi-transparent which offers a variety of uses not applicable to glass-based systems, and most of the materials used are low-cost. In practice it has ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Carbon Nanotubes
A scanning tunneling microscopy image of a single-walled carbon nanotube Rotating single-walled zigzag carbon nanotube A carbon nanotube (CNT) is a tube made of carbon with diameters typically measured in nanometers. ''Single-wall carbon nanotubes'' (''SWCNTs'') are one of the allotropes of carbon, intermediate between fullerene cages and flat graphene, with diameters in the range of a nanometre. Although not made this way, single-wall carbon nanotubes can be idealized as cutouts from a two-dimensional Hexagonal tiling, hexagonal lattice of carbon atoms rolled up along one of the Bravais lattice vectors of the hexagonal lattice to form a hollow cylinder. In this construction, periodic boundary conditions are imposed over the length of this roll-up vector to yield a helical lattice of seamlessly bonded carbon atoms on the cylinder surface. ''Multi-wall carbon nanotubes'' (''MWCNTs'') consisting of nested single-wall carbon nanotubes weakly bound together by van der Waals i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Effective Mass (solid-state Physics)
In solid state physics, a particle's effective mass (often denoted m^*) is the mass that it ''seems'' to have when responding to forces, or the mass that it seems to have when interacting with other identical particles in a thermal distribution. One of the results from the band theory of solids is that the movement of particles in a periodic potential, over long distances larger than the lattice spacing, can be very different from their motion in a vacuum. The effective mass is a quantity that is used to simplify band structures by modeling the behavior of a free particle with that mass. For some purposes and some materials, the effective mass can be considered to be a simple constant of a material. In general, however, the value of effective mass depends on the purpose for which it is used, and can vary depending on a number of factors. For electrons or electron holes in a solid, the effective mass is usually stated as a factor multiplying the rest mass of an electron, ''m'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Internal Chemical Potential
In thermodynamics, the chemical potential of a species is the energy that can be absorbed or released due to a change of the particle number of the given species, e.g. in a chemical reaction or phase transition. The chemical potential of a species in a mixture is defined as the rate of change of free energy of a thermodynamic system with respect to the change in the number of atoms or molecules of the species that are added to the system. Thus, it is the partial derivative of the free energy with respect to the amount of the species, all other species' concentrations in the mixture remaining constant. When both temperature and pressure are held constant, and the number of particles is expressed in moles, the chemical potential is the partial molar Gibbs free energy. At chemical equilibrium or in phase equilibrium, the total sum of the product of chemical potentials and stoichiometric coefficients is zero, as the free energy is at a minimum. In a system in diffusion equilibrium, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
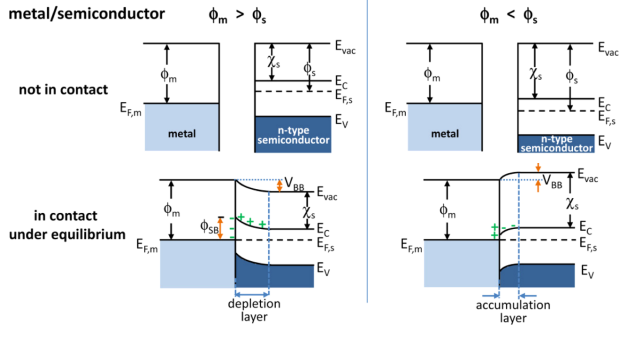
Band Bending
In solid-state physics, band bending refers to the process in which the electronic band structure in a material curves up or down near a junction or interface. It does not involve any physical (spatial) bending. When the electrochemical potential of the free charge carriers around an interface of a semiconductor is dissimilar, charge carriers are transferred between the two materials until an equilibrium state is reached whereby the potential difference vanishes. The band bending concept was first developed in 1938 when Mott, Davidov and Schottky all published theories of the rectifying effect of metal-semiconductor contacts. The use of semiconductor junctions sparked the computer revolution in 1990. Devices such as the diode, the transistor, the photocell and many more still play an important role in technology. Qualitative description Band bending can be induced by several types of contact. In this section metal-semiconductor contact, surface state, applied bias and adsorption ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thomas–Fermi Screening
Thomas–Fermi screening is a theoretical approach to calculate the effects of electric field screening by electrons in a solid.N. W. Ashcroft and N. D. Mermin, ''Solid State Physics'' (Thomson Learning, Toronto, 1976) It is a special case of the more general Lindhard theory; in particular, Thomas–Fermi screening is the limit of the Lindhard formula when the wavevector (the reciprocal of the length-scale of interest) is much smaller than the Fermi wavevector, i.e. the long-distance limit. It is named after Llewellyn Thomas and Enrico Fermi. The Thomas–Fermi wavevector (in Gaussian-cgs units) is k_0^2 = 4\pi e^2 \frac, where ''μ'' is the chemical potential ( Fermi level), ''n'' is the electron concentration and ''e'' is the elementary charge. Under many circumstances, including semiconductors that are not too heavily doped, , where ''k''B is Boltzmann constant and ''T'' is temperature. In this case, k_0^2 = \frac, i.e. is given by the familiar formula for Debye length. In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |