|
Proportional (fair Division)
A proportional division is a kind of fair division in which a resource is divided among ''n'' partners with subjective valuations, giving each partner at least 1/''n'' of the resource by his/her own subjective valuation. Proportionality was the first fairness criterion studied in the literature; hence it is sometimes called "simple fair division". It was first conceived by Steinhaus. Example Consider a land asset that has to be divided among 3 heirs: Alice and Bob who think that it's worth 3 million dollars, and George who thinks that it's worth $4.5M. In a proportional division, Alice receives a land-plot that she believes to be worth at least $1M, Bob receives a land-plot that ''he'' believes to be worth at least $1M (even though Alice may think it is worth less), and George receives a land-plot that he believes to be worth at least $1.5M. Existence A proportional division does not always exist. For example, if the resource contains several indivisible items and the number ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fair Division
Fair division is the problem in game theory of dividing a set of resources among several people who have an entitlement to them so that each person receives their due share. That problem arises in various real-world settings such as division of inheritance, partnership dissolutions, divorce settlements, electronic frequency allocation, airport traffic management, and exploitation of Earth observation satellites. It is an active research area in mathematics, economics (especially social choice theory), dispute resolution, etc. The central tenet of fair division is that such a division should be performed by the players themselves, maybe using a mediator but certainly not an arbiter as only the players really know how they value the goods. The archetypal fair division algorithm is divide and choose. It demonstrates that two agents with different tastes can divide a cake such that each of them believes that he got the best piece. The research in fair division can be seen as an exten ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fair Cake-cutting
Fair cake-cutting is a kind of fair division problem. The problem involves a ''heterogeneous'' resource, such as a cake with different toppings, that is assumed to be ''divisible'' – it is possible to cut arbitrarily small pieces of it without destroying their value. The resource has to be divided among several partners who have different preferences over different parts of the cake, i.e., some people prefer the chocolate toppings, some prefer the cherries, some just want as large a piece as possible. The division should be ''unanimously'' fair - each person should receive a piece that he or she believes to be a fair share. The "cake" is only a metaphor; procedures for fair cake-cutting can be used to divide various kinds of resources, such as land estates, advertisement space or broadcast time. The prototypical procedure for fair cake-cutting is divide and choose, which is mentioned already in the book of Genesis. It solves the fair division problem for two people. The modern ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proportional Cake-cutting
A proportional cake-cutting is a kind of fair cake-cutting. It is a division of a heterogeneous resource ("cake") that satisfies the proportionality criterion, namely, that every partner feels that his allocated share is worth at least 1/''n'' of the total. Two assumptions are usually made when proportionality is discussed: * The valuations of the partners are ''non-atomic'', i.e., there are no indivisible elements with positive value. * The valuations of the partners are ''additive'', i.e., when a piece is divided, the value of the piece is equal to the sum of its parts. Formal definitions The cake is denoted by C. There are n people. Each person i has a value function V_i. A partition of the cake, X_1\sqcup \cdots \sqcup X_n = C, is called ''proportional'' if:V_i(X_i) \ge V_i(C)/n for every person i \in \. Procedures For two people, divide and choose is the classic solution. One person divides the resource into what they believe are equal halves, and the other person ch ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Super-proportional Division
A strongly-proportional division (sometimes called super-proportional division) is a kind of a fair division. It is a division of resources among ''n'' partners, in which the value received by each partner is strictly more than his/her due share of 1/''n'' of the total value. Formally, in a strongly-proportional division of a resource ''C'' among ''n'' partners, each partner ''i'', with value measure ''Vi'', receives a share ''Xi'' such thatV_i(X_i) > V_i(C)/n.Obviously, a strongly-proportional division does not exist when all partners have the same value measure. The best condition that can ''always'' be guaranteed is V_i(X_i) \geq V_i(C)/n, which is the condition for a plain proportional division. However, one may hope that, when different agents have different valuations, it may be possible to use this fact for the benefit of all players, and give each of them strictly more than their due share. Existence In 1948, Hugo Steinhaus conjectured the existence of a super-proportiona ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Individual Rationality
Rational choice theory refers to a set of guidelines that help understand economic and social behaviour. The theory originated in the eighteenth century and can be traced back to political economist and philosopher, Adam Smith. The theory postulates that an individual will perform a cost-benefit analysis to determine whether an option is right for them.Gary Browning, Abigail Halcli, Frank Webster (2000). ''Understanding Contemporary Society: Theories of the Present'', London: SAGE Publications. It also suggests that an individual's self-driven rational actions will help better the overall economy. Rational choice theory looks at three concepts: rational actors, self interest and the invisible hand. Rationality can be used as an assumption for the behaviour of individuals in a wide range of contexts outside of economics. It is also used in political science, sociology, and philosophy. Overview The basic premise of rational choice theory is that the decisions made by individual ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
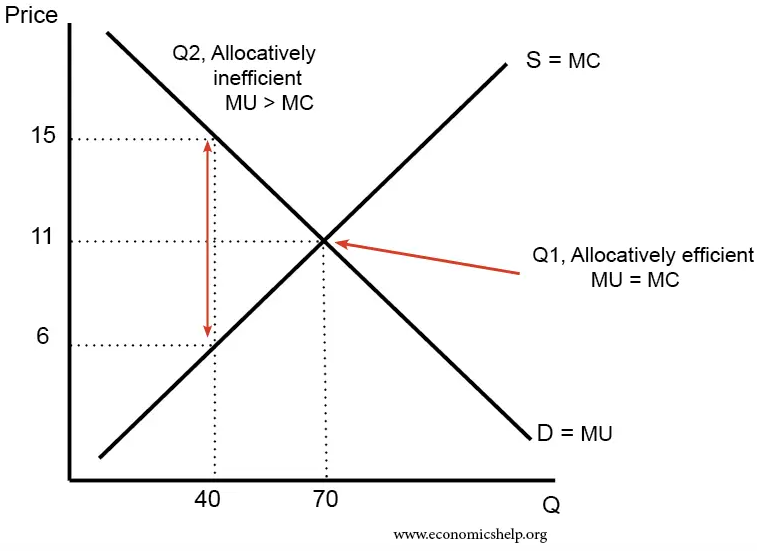
Allocative Efficiency
Allocative efficiency is a state of the economy in which production is aligned with consumer preferences; in particular, every good or service is produced up to the point where the last unit provides a marginal benefit to consumers equal to the marginal cost of producing. Description In contract theory, allocative efficiency is achieved in a contract in which the skill demanded by the offering party and the skill of the agreeing party are the same. Resource allocation efficiency includes two aspects: # At the macro aspect, it is the allocation efficiency of social resources, which is achieved through the economic system arrangements of the entire society. # The micro aspect is the use efficiency of resources, which can be understood as the production efficiency of the organization, which can be improved through innovation and progress within the organizations. Although there are different standards of evaluation for the concept of allocative efficiency, the basic principle ass ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fair Cake-cutting
Fair cake-cutting is a kind of fair division problem. The problem involves a ''heterogeneous'' resource, such as a cake with different toppings, that is assumed to be ''divisible'' – it is possible to cut arbitrarily small pieces of it without destroying their value. The resource has to be divided among several partners who have different preferences over different parts of the cake, i.e., some people prefer the chocolate toppings, some prefer the cherries, some just want as large a piece as possible. The division should be ''unanimously'' fair - each person should receive a piece that he or she believes to be a fair share. The "cake" is only a metaphor; procedures for fair cake-cutting can be used to divide various kinds of resources, such as land estates, advertisement space or broadcast time. The prototypical procedure for fair cake-cutting is divide and choose, which is mentioned already in the book of Genesis. It solves the fair division problem for two people. The modern ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perfect Division
Exact division, also called consensus division, is a partition of a continuous resource (" cake") into some ''k'' pieces, such that each of ''n'' people with different tastes agree on the value of each of the pieces. For example, consider a cake which is half chocolate and half vanilla. Alice values only the chocolate and George values only the vanilla. The cake is divided into three pieces: one piece contains 20% of the chocolate and 20% of the vanilla, the second contains 50% of the chocolate and 50% of the vanilla, and the third contains the rest of the cake. This is an exact division (with ''k''=3 and ''n''=2), as both Alice and George value the three pieces as 20%, 50% and 30% respectively. Several common variants and special cases are known by different terms: * Consensus halving – the cake should be partitioned into two pieces (''k''=2), and all agents agree that the pieces have equal values. *Consensus 1/''k''-division, for any constant ''k''>1 - the cake should be partition ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inequity Aversion
Inequity aversion (IA) is the preference for fairness and resistance to incidental inequalities. The social sciences that study inequity aversion include sociology, economics, psychology, anthropology, and ethology. Human studies Inequity aversion research on humans mostly occurs in the discipline of economics though it is also studied in sociology. Research on inequity aversion began in 1978 when studies suggested that humans are sensitive to inequities in favor of as well as those against them, and that some people attempt overcompensation when they feel "guilty" or unhappy to have received an undeserved reward. A more recent definition of inequity aversion (resistance to inequitable outcomes) was developed in 1999 by Fehr and Schmidt. They postulated that people make decisions so as to minimize inequity in outcomes. Specifically, consider a setting with individuals who receive pecuniary outcomes ''xi''. Then the utility to person ''i'' would be given by :U_i(\) = x_i - \frac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpg)