|
Prismatoid
In geometry, a prismatoid is a polyhedron whose vertices all lie in two parallel planes. Its lateral faces can be trapezoids or triangles. If both planes have the same number of vertices, and the lateral faces are either parallelograms or trapezoids, it is called a prismoid. Volume If the areas of the two parallel faces are and , the cross-sectional area of the intersection of the prismatoid with a plane midway between the two parallel faces is , and the height (the distance between the two parallel faces) is , then the volume of the prismatoid is given by V = \fracB. E. Meserve, R. E. Pingry: ''Some Notes on the Prismoidal Formula''. The Mathematics Teacher, Vol. 45, No. 4 (April 1952), pp. 257-263 (This formula follows immediately by integrating the area parallel to the two planes of vertices by Simpson's rule, since that rule is exact for integration of polynomials of degree up to 3, and in this case the area is at most a quadratic function in the height.) Prismatoid famil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prismatoid (parameters H,A₁,A₂,A₃)
In geometry, a prismatoid is a polyhedron whose vertices all lie in two parallel planes. Its lateral faces can be trapezoids or triangles. If both planes have the same number of vertices, and the lateral faces are either parallelograms or trapezoids, it is called a prismoid. Volume If the areas of the two parallel faces are and , the cross-sectional area of the intersection of the prismatoid with a plane midway between the two parallel faces is , and the height (the distance between the two parallel faces) is , then the volume of the prismatoid is given by V = \fracB. E. Meserve, R. E. Pingry: ''Some Notes on the Prismoidal Formula''. The Mathematics Teacher, Vol. 45, No. 4 (April 1952), pp. 257-263 (This formula follows immediately by integrating the area parallel to the two planes of vertices by Simpson's rule, since that rule is exact for integration of polynomials of degree up to 3, and in this case the area is at most a quadratic function in the height.) Prismatoid fam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pyramid (geometry)
In geometry, a pyramid () is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle, called a ''lateral face''. It is a conic solid with polygonal base. A pyramid with an base has vertices, faces, and edges. All pyramids are self-dual. A right pyramid has its apex directly above the centroid of its base. Nonright pyramids are called oblique pyramids. A regular pyramid has a regular polygon base and is usually implied to be a ''right pyramid''. When unspecified, a pyramid is usually assumed to be a ''regular'' square pyramid, like the physical pyramid structures. A triangle-based pyramid is more often called a tetrahedron. Among oblique pyramids, like acute and obtuse triangles, a pyramid can be called ''acute'' if its apex is above the interior of the base and ''obtuse'' if its apex is above the exterior of the base. A right-angled pyramid has its apex above an edge or vertex of the base. In a tetrahedro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cupola (geometry)
In geometry, a cupola is a solid formed by joining two polygons, one (the base) with twice as many edges as the other, by an alternating band of isosceles triangles and rectangles. If the triangles are equilateral and the rectangles are squares, while the base and its opposite face are regular polygons, the triangular, square, and pentagonal cupolae all count among the Johnson solids, and can be formed by taking sections of the cuboctahedron, rhombicuboctahedron, and rhombicosidodecahedron, respectively. A cupola can be seen as a prism where one of the polygons has been collapsed in half by merging alternate vertices. A cupola can be given an extended Schläfli symbol representing a regular polygon joined by a parallel of its truncation, or Cupolae are a subclass of the prismatoids. Its dual contains a shape that is sort of a weld between half of an -sided trapezohedron and a -sided pyramid. Examples The above-mentioned three polyhedra are the only non-trivial convex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Star Antiprism
In geometry, an antiprism or is a polyhedron composed of two parallel direct copies (not mirror images) of an polygon, connected by an alternating band of triangles. They are represented by the Conway notation . Antiprisms are a subclass of prismatoids, and are a (degenerate) type of snub polyhedron. Antiprisms are similar to prisms, except that the bases are twisted relatively to each other, and that the side faces (connecting the bases) are triangles, rather than quadrilaterals. The dual polyhedron of an -gonal antiprism is an -gonal trapezohedron. History At the intersection of modern-day graph theory and coding theory, the triangulation of a set of points have interested mathematicians since Isaac Newton, who fruitlessly sought a mathematical proof of the kissing number problem in 1694. The existence of antiprisms was discussed, and their name was coined by Johannes Kepler, though it is possible that they were previously known to Archimedes, as they satisf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallelepiped 2013-11-29
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms (the term ''rhomboid'' is also sometimes used with this meaning). By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, the four concepts—''parallelepiped'' and ''cube'' in three dimensions, ''parallelogram'' and ''square'' in two dimensions—are defined, but in the context of a more general affine geometry, in which angles are not differentiated, only ''parallelograms'' and ''parallelepipeds'' exist. Three equivalent definitions of ''parallelepiped'' are *a polyhedron with six faces (hexahedron), each of which is a parallelogram, *a hexahedron with three pairs of parallel faces, and *a prism of which the base is a parallelogram. The rectangular cuboid (six rectangular faces), cube (six square faces), and the rhombohedron (six rhombus faces) are all specific cases of parallelepiped. "Parallelepiped" is now usually pronounced or ; trad ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frustum
In geometry, a (from the Latin for "morsel"; plural: ''frusta'' or ''frustums'') is the portion of a solid (normally a pyramid or a cone) that lies between two parallel planes cutting this solid. In the case of a pyramid, the base faces are polygonal, the side faces are trapezoidal. A right frustum is a right pyramid or a right cone truncated perpendicularly to its axis; otherwise it is an oblique frustum. If all its edges are forced to become of the same length, then a frustum becomes a prism (possibly oblique or/and with irregular bases). In computer graphics, the viewing frustum is the three-dimensional region which is visible on the screen. It is formed by a clipped pyramid; in particular, ''frustum culling'' is a method of hidden surface determination. In the aerospace industry, a frustum is the fairing between two stages of a multistage rocket (such as the Saturn V), which is shaped like a truncated cone. Elements, special cases, and related concepts A frustu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cupola (geometry)
In geometry, a cupola is a solid formed by joining two polygons, one (the base) with twice as many edges as the other, by an alternating band of isosceles triangles and rectangles. If the triangles are equilateral and the rectangles are squares, while the base and its opposite face are regular polygons, the triangular, square, and pentagonal cupolae all count among the Johnson solids, and can be formed by taking sections of the cuboctahedron, rhombicuboctahedron, and rhombicosidodecahedron, respectively. A cupola can be seen as a prism where one of the polygons has been collapsed in half by merging alternate vertices. A cupola can be given an extended Schläfli symbol representing a regular polygon joined by a parallel of its truncation, or Cupolae are a subclass of the prismatoids. Its dual contains a shape that is sort of a weld between half of an -sided trapezohedron and a -sided pyramid. Examples The above-mentioned three polyhedra are the only non-trivial convex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antiprism
In geometry, an antiprism or is a polyhedron composed of two parallel direct copies (not mirror images) of an polygon, connected by an alternating band of triangles. They are represented by the Conway notation . Antiprisms are a subclass of prismatoids, and are a (degenerate) type of snub polyhedron. Antiprisms are similar to prisms, except that the bases are twisted relatively to each other, and that the side faces (connecting the bases) are triangles, rather than quadrilaterals. The dual polyhedron of an -gonal antiprism is an -gonal trapezohedron. History At the intersection of modern-day graph theory and coding theory, the triangulation of a set of points have interested mathematicians since Isaac Newton, who fruitlessly sought a mathematical proof of the kissing number problem in 1694. The existence of antiprisms was discussed, and their name was coined by Johannes Kepler, though it is possible that they were previously known to Archimedes, as they satisfy the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallelepiped
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms (the term ''rhomboid'' is also sometimes used with this meaning). By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, the four concepts—''parallelepiped'' and ''cube'' in three dimensions, ''parallelogram'' and ''square'' in two dimensions—are defined, but in the context of a more general affine geometry, in which angles are not differentiated, only ''parallelograms'' and ''parallelepipeds'' exist. Three equivalent definitions of ''parallelepiped'' are *a polyhedron with six faces (hexahedron), each of which is a parallelogram, *a hexahedron with three pairs of parallel faces, and *a prism of which the base is a parallelogram. The rectangular cuboid (six rectangular faces), cube (six square faces), and the rhombohedron (six rhombus faces) are all specific cases of parallelepiped. "Parallelepiped" is now usually pronounced or ; ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
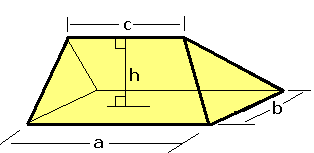
Wedge (geometry)
In solid geometry, a wedge is a polyhedron defined by two triangles and three trapezoid faces. A wedge has five faces, nine edges, and six vertices. A wedge is a subclass of the prismatoids with the base and opposite ridge in two parallel planes. A wedge can also be classified as a digonal cupola. Comparisons: * A wedge is a parallelepiped where a face has collapsed into a line. * A quadrilaterally-based pyramid is a wedge in which one of the edges between two trapezoid faces has collapsed into a point. Volume For a rectangle based wedge, the volume is :V = bh\left(\frac+\frac\right), where the base rectangle is ''a'' by ''b'', ''c'' is the apex edge length parallel to ''a'', and ''h'' the height from the base rectangle to the apex edge. Examples Wedges can be created from decomposition of other polyhedra. For instance, the dodecahedron can be divided into a central cube with 6 wedges covering the cube faces. The orientations of the wedges are such that the triangle and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prism (geometry)
In geometry, a prism is a polyhedron comprising an polygon Base (geometry), base, a second base which is a Translation (geometry), translated copy (rigidly moved without rotation) of the first, and other Face (geometry), faces, necessarily all parallelograms, joining corresponding sides of the two bases. All Cross section (geometry), cross-sections parallel to the bases are translations of the bases. Prisms are named after their bases, e.g. a prism with a pentagonal base is called a pentagonal prism. Prisms are a subclass of prismatoids. Like many basic geometric terms, the word ''prism'' () was first used in Euclid's Elements. Euclid defined the term in Book XI as “a solid figure contained by two opposite, equal and parallel planes, while the rest are parallelograms”. However, this definition has been criticized for not being specific enough in relation to the nature of the bases, which caused confusion among later geometry writers. Oblique prism An oblique prism is a pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polynomial
In mathematics, a polynomial is an expression consisting of indeterminates (also called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An example of a polynomial of a single indeterminate is . An example with three indeterminates is . Polynomials appear in many areas of mathematics and science. For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problems to complicated scientific problems; they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics and social science; they are used in calculus and numerical analysis to approximate other functions. In advanced mathematics, polynomials are used to construct polynomial rings and algebraic varieties, which are central concepts in algebra and algebraic geometry. Etymology The word ''polynomial'' join ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |