|
Positive Mass Theorem
The positive energy theorem (also known as the positive mass theorem) refers to a collection of foundational results in general relativity and differential geometry. Its standard form, broadly speaking, asserts that the gravitational energy of an isolated system is nonnegative, and can only be zero when the system has no gravitating objects. Although these statements are often thought of as being primarily physical in nature, they can be formalized as mathematical theorems which can be proven using techniques of differential geometry, partial differential equations, and geometric measure theory. Richard Schoen and Shing-Tung Yau, in 1979 and 1981, were the first to give proofs of the positive mass theorem. Edward Witten, in 1982, gave the outlines of an alternative proof, which were later filled in rigorously by mathematicians. Witten and Yau were awarded the Fields medal in mathematics in part for their work on this topic. An imprecise formulation of the Schoen-Yau / Witten posi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
General Relativity
General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics. General relativity generalizes special relativity and refines Newton's law of universal gravitation, providing a unified description of gravity as a geometric property of space and time or four-dimensional spacetime. In particular, the ' is directly related to the energy and momentum of whatever matter and radiation are present. The relation is specified by the Einstein field equations, a system of second order partial differential equations. Newton's law of universal gravitation, which describes classical gravity, can be seen as a prediction of general relativity for the almost flat spacetime geometry around stationary mass distributions. Some predictions of general relativity, however, are beyond Newton's law of universal gravitat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
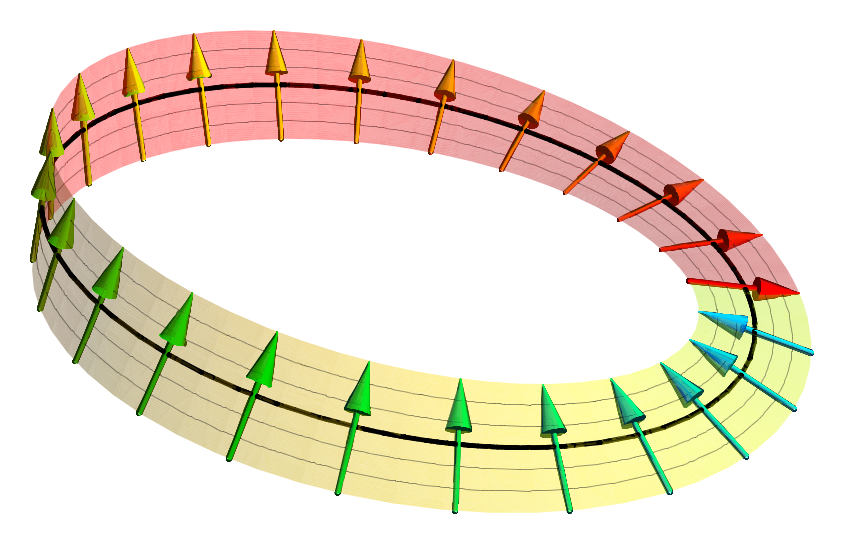
Spinor
In geometry and physics, spinors are elements of a complex vector space that can be associated with Euclidean space. Like geometric vectors and more general tensors, spinors transform linearly when the Euclidean space is subjected to a slight (infinitesimal) rotation. Unlike vectors and tensors, a spinor transforms to its negative when the space is continuously rotated through a complete turn from 0° to 360° (see picture). This property characterizes spinors: spinors can be viewed as the "square roots" of vectors (although this is inaccurate and may be misleading; they are better viewed as "square roots" of sections of vector bundles – in the case of the exterior algebra bundle of the cotangent bundle, they thus become "square roots" of differential forms). It is also possible to associate a substantially similar notion of spinor to Minkowski space, in which case the Lorentz transformations of special relativity play the role of rotations. Spinors were introduced in geome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Achilles Papapetrou
Achille Papapetrou ( el, Αχιλλέας Νικολάου Παπαπέτρου; February 2, 1907 – August 12, 1997) was a Greek theoretical physicist, who contributed to the general theory of relativity. He is known for the Mathisson–Papapetrou–Dixon equations, the Majumdar–Papapetrou solution, and the Weyl−Lewis−Papapetrou coordinates of gravity theory. He worked on exact solutions of Einstein's field equations and long sought a solution for rotating masses, which, however, were only found by Roy Kerr. Papapetrou was then the first who recognized and jubilantly welcomed Kerr's breakthrough announced at the Texas Symposium on Relativistic Astrophysics, Dallas, December 1963. Early life and education Papapetrou was born in Irakleia Serres in Northern Greece (Macedonia province), on February 2, 1907. His father was a schoolteacher. During World War I, his family was deported from Serres, but returned at the end of the war. From 1925, Papapetrou studied mechani ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sudhansu Datta Majumdar
Sudhansu Datta Majumdar (1915 – 1997) was an Indian physicist, and faculty member of the Indian Institute of Technology, Kharagpur. Biography Born in 1915 in Sylhet (now in Bangladesh), Sudhansu Datta Majumdar had his education in Sylhet; Presidency College, Calcutta, and University College of Science also called Rajabazar Science College, Calcutta University. In an academic career spanning several decades, he served in different capacities in various institutions. Beginning with a stint in the Palit Laboratory of Physics, Rajabazar Science College, Calcutta University, from where he wrote the now famous Majumdar–Papapetrou paper, he was appointed Lecturer in Physics in Calcutta University in 1951. Subsequently, he became a reader there in 1960. During 1956–57, he went to Cambridge University, United Kingdom, on an educational tour to interact with P. A. M. Dirac. In 1962, Majumdar obtained the rare honour of the degree of D.Sc. in Physics from Sc. College, Calcutta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gaussian Units
Gaussian units constitute a metric system of physical units. This system is the most common of the several electromagnetic unit systems based on cgs (centimetre–gram–second) units. It is also called the Gaussian unit system, Gaussian-cgs units, or often just cgs units. The term "cgs units" is ambiguous and therefore to be avoided if possible: there are several variants of cgs with conflicting definitions of electromagnetic quantities and units. SI units predominate in most fields, and continue to increase in popularity at the expense of Gaussian units. Alternative unit systems also exist. Conversions between quantities in Gaussian and SI units are direct unit conversions, because the quantities themselves are defined differently in each system. This means that the equations expressing physical laws of electromagnetism—such as Maxwell's—will change depending on the system of units employed. As an example, quantities that are dimensionless in one system may have dimension i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magnetic Charge
In particle physics, a magnetic monopole is a hypothetical elementary particle that is an isolated magnet with only one magnetic pole (a north pole without a south pole or vice versa). A magnetic monopole would have a net north or south "magnetic charge". Modern interest in the concept stems from particle theories, notably the grand unified and superstring theories, which predict their existence. The known elementary particles that have electric charge are electric monopoles. Magnetism in bar magnets and electromagnets is not caused by magnetic monopoles, and indeed, there is no known experimental or observational evidence that magnetic monopoles exist. Some condensed matter systems contain effective (non-isolated) magnetic monopole quasi-particles, or contain phenomena that are mathematically analogous to magnetic monopoles. Historical background Early science and classical physics Many early scientists attributed the magnetism of lodestones to two different "magnetic flu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electric Charge
Electric charge is the physical property of matter that causes charged matter to experience a force when placed in an electromagnetic field. Electric charge can be ''positive'' or ''negative'' (commonly carried by protons and electrons respectively). Like charges repel each other and unlike charges attract each other. An object with an absence of net charge is referred to as neutral. Early knowledge of how charged substances interact is now called classical electrodynamics, and is still accurate for problems that do not require consideration of quantum effects. Electric charge is a conserved property; the net charge of an isolated system, the amount of positive charge minus the amount of negative charge, cannot change. Electric charge is carried by subatomic particles. In ordinary matter, negative charge is carried by electrons, and positive charge is carried by the protons in the nuclei of atoms. If there are more electrons than protons in a piece of matter, it will have ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Einstein Field Equations
In the general theory of relativity, the Einstein field equations (EFE; also known as Einstein's equations) relate the geometry of spacetime to the distribution of matter within it. The equations were published by Einstein in 1915 in the form of a tensor equation which related the local ' (expressed by the Einstein tensor) with the local energy, momentum and stress within that spacetime (expressed by the stress–energy tensor). Analogously to the way that electromagnetic fields are related to the distribution of charges and currents via Maxwell's equations, the EFE relate the spacetime geometry to the distribution of mass–energy, momentum and stress, that is, they determine the metric tensor of spacetime for a given arrangement of stress–energy–momentum in the spacetime. The relationship between the metric tensor and the Einstein tensor allows the EFE to be written as a set of nonlinear partial differential equations when used in this way. The solutions of the EFE are t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anti-de Sitter Spacetime
In mathematics and physics, ''n''-dimensional anti-de Sitter space (AdS''n'') is a maximally symmetric Lorentzian manifold with constant negative scalar curvature. Anti-de Sitter space and de Sitter space are named after Willem de Sitter (1872–1934), professor of astronomy at Leiden University and director of the Leiden Observatory. Willem de Sitter and Albert Einstein worked together closely in Leiden in the 1920s on the spacetime structure of the universe. Manifolds of constant curvature are most familiar in the case of two dimensions, where the elliptic plane or surface of a sphere is a surface of constant positive curvature, a flat (i.e., Euclidean) plane is a surface of constant zero curvature, and a hyperbolic plane is a surface of constant negative curvature. Einstein's general theory of relativity places space and time on equal footing, so that one considers the geometry of a unified spacetime instead of considering space and time separately. The cases of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gary Gibbons
Gary William Gibbons (born 1 July 1946) is a British theoretical physicist. Education Gibbons was born in Coulsdon, Surrey. He was educated at Purley County Grammar School and the University of Cambridge, where in 1969 he became a research student under the supervision of Dennis Sciama. When Sciama moved to the University of Oxford, he became a student of Stephen Hawking, obtaining his PhD from Cambridge in 1973. Career and research Apart from a stay at the Max Planck Institute in Munich in the 1970s he has remained in Cambridge throughout his career, becoming a full professor in 1997, a Fellow of the Royal Society in 1999, and a Fellow of Trinity College, Cambridge in 2002. Having worked on classical general relativity for his PhD thesis, Gibbons focused on the quantum theory of black holes afterwards. Together with Malcolm Perry, he used thermal Green's functions to prove the universality of thermodynamic properties of horizons, including cosmological event horizons. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Malcolm Perry (physicist)
Malcolm John Perry (born 13 November 1951) is a British theoretical physicist and emeritus professor of theoretical physics at University of Cambridge and professor of theoretical physics at Queen Mary University of London. His research mainly concerns quantum gravity, black holes, general relativity, and supergravity. Biography Perry attended King Edward's School, Birmingham before reading physics at St John's College, Oxford. He was a graduate student at King's College, Cambridge, under the supervision of Stephen Hawking. He obtained his doctorate in 1978 with a thesis on the quantum mechanics of black holes. In these early years, he worked on several very influential papers on Euclidean quantum gravity and black hole radiation with Gary Gibbons and Hawking. After his graduate studies, he worked in Princeton, New Jersey from 1978 to 1986. With his student Rob Myers, he found the Myers-Perry metric, which describes the higher-dimensional generalization of the Kerr metric. H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |