|
Polyphase Matrix
In signal processing, a polyphase matrix is a matrix whose elements are filter masks. It represents a filter bank as it is used in sub-band coders alias discrete wavelet transforms. If \scriptstyle h,\, g are two filters, then one level the traditional wavelet transform maps an input signal \scriptstyle a_0 to two output signals \scriptstyle a_1,\, d_1, each of the half length: :\begin a_1 &= (h \cdot a_0) \downarrow 2 \\ d_1 &= (g \cdot a_0) \downarrow 2 \end Note, that the dot means polynomial multiplication; i.e., convolution and \scriptstyle\downarrow means downsampling. If the above formula is implemented directly, you will compute values that are subsequently flushed by the down-sampling. You can avoid their computation by splitting the filters and the signal into even and odd indexed values before the wavelet transformation: :\begin h_\mbox &= h \downarrow 2 & a_ &= a_0 \downarrow 2 \\ h_\mbox &= (h \leftarrow 1) \downarrow 2 & a_ &= (a_0 \leftarro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
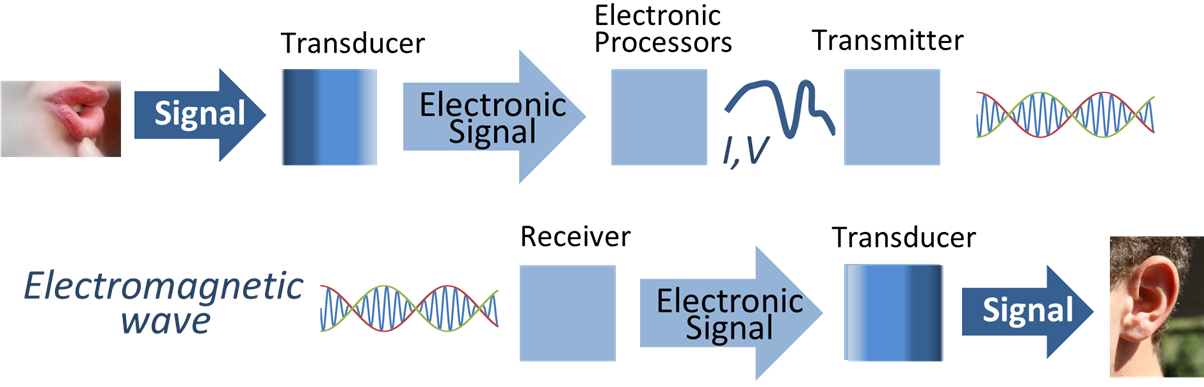
Signal Processing
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as audio signal processing, sound, image processing, images, and scientific measurements. Signal processing techniques are used to optimize transmissions, Data storage, digital storage efficiency, correcting distorted signals, subjective video quality and to also detect or pinpoint components of interest in a measured signal. History According to Alan V. Oppenheim and Ronald W. Schafer, the principles of signal processing can be found in the classical numerical analysis techniques of the 17th century. They further state that the digital refinement of these techniques can be found in the digital control systems of the 1940s and 1950s. In 1948, Claude Shannon wrote the influential paper "A Mathematical Theory of Communication" which was published in the Bell System Technical Journal. The paper laid the groundwork for later development of information c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverse Matrix
In linear algebra, an -by- square matrix is called invertible (also nonsingular or nondegenerate), if there exists an -by- square matrix such that :\mathbf = \mathbf = \mathbf_n \ where denotes the -by- identity matrix and the multiplication used is ordinary matrix multiplication. If this is the case, then the matrix is uniquely determined by , and is called the (multiplicative) ''inverse'' of , denoted by . Matrix inversion is the process of finding the matrix that satisfies the prior equation for a given invertible matrix . A square matrix that is ''not'' invertible is called singular or degenerate. A square matrix is singular if and only if its determinant is zero. Singular matrices are rare in the sense that if a square matrix's entries are randomly selected from any finite region on the number line or complex plane, the probability that the matrix is singular is 0, that is, it will "almost never" be singular. Non-square matrices (-by- matrices for which ) do not hav ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix Decomposition
In the mathematical discipline of linear algebra, a matrix decomposition or matrix factorization is a factorization of a matrix into a product of matrices. There are many different matrix decompositions; each finds use among a particular class of problems. Example In numerical analysis, different decompositions are used to implement efficient matrix algorithms. For instance, when solving a system of linear equations A \mathbf = \mathbf, the matrix ''A'' can be decomposed via the LU decomposition. The LU decomposition factorizes a matrix into a lower triangular matrix ''L'' and an upper triangular matrix ''U''. The systems L(U \mathbf) = \mathbf and U \mathbf = L^ \mathbf require fewer additions and multiplications to solve, compared with the original system A \mathbf = \mathbf, though one might require significantly more digits in inexact arithmetic such as floating point. Similarly, the QR decomposition expresses ''A'' as ''QR'' with ''Q'' an orthogonal matrix and ''R'' an upp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Norm
In mathematics, a matrix norm is a vector norm in a vector space whose elements (vectors) are matrices (of given dimensions). Preliminaries Given a field K of either real or complex numbers, let K^ be the -vector space of matrices with m rows and n columns and entries in the field K. A matrix norm is a norm on K^. This article will always write such norms with double vertical bars (like so: \, A\, ). Thus, the matrix norm is a function \, \cdot\, : K^ \to \R that must satisfy the following properties: For all scalars \alpha \in K and matrices A, B \in K^, *\, A\, \ge 0 (''positive-valued'') *\, A\, = 0 \iff A=0_ (''definite'') *\left\, \alpha A\right\, =\left, \alpha\ \left\, A\right\, (''absolutely homogeneous'') *\, A+B\, \le \, A\, +\, B\, (''sub-additive'' or satisfying the ''triangle inequality'') The only feature distinguishing matrices from rearranged vectors is multiplication. Matrix norms are particularly useful if they are also sub-multiplicative: *\left\, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Radius
In mathematics, the spectral radius of a square matrix is the maximum of the absolute values of its eigenvalues. More generally, the spectral radius of a bounded linear operator is the supremum of the absolute values of the elements of its spectrum. The spectral radius is often denoted by . Definition Matrices Let be the eigenvalues of a matrix . The spectral radius of is defined as :\rho(A) = \max \left \. The spectral radius can be thought of as an infimum of all norms of a matrix. Indeed, on the one hand, \rho(A) \leqslant \, A\, for every natural matrix norm \, \cdot\, ; and on the other hand, Gelfand's formula states that \rho(A) = \lim_ \, A^k\, ^ . Both of these results are shown below. However, the spectral radius does not necessarily satisfy \, A\mathbf\, \leqslant \rho(A) \, \mathbf\, for arbitrary vectors \mathbf \in \mathbb^n . To see why, let r > 1 be arbitrary and consider the matrix : C_r = \begin 0 & r^ \\ r & 0 \end . The characteristic polynomial ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Z Transform
In mathematics and signal processing, the Z-transform converts a discrete-time signal, which is a sequence of real or complex numbers, into a complex frequency-domain (z-domain or z-plane) representation. It can be considered as a discrete-time equivalent of the Laplace transform (s-domain). This similarity is explored in the theory of time-scale calculus. Whereas the continuous-time Fourier transform is evaluated on the Laplace s-domain's imaginary line, the discrete-time Fourier transform is evaluated over the unit circle of the z-domain. What is roughly the s-domain's left half-plane, is now the inside of the complex unit circle; what is the z-domain's outside of the unit circle, roughly corresponds to the right half-plane of the s-domain. One of the means of designing digital filters is to take analog designs, subject them to a bilinear transform which maps them from the s-domain to the z-domain, and then produce the digital filter by inspection, manipulation, or numeri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frobenius Norm
In mathematics, a matrix norm is a vector norm in a vector space whose elements (vectors) are matrices (of given dimensions). Preliminaries Given a field K of either real or complex numbers, let K^ be the -vector space of matrices with m rows and n columns and entries in the field K. A matrix norm is a norm on K^. This article will always write such norms with double vertical bars (like so: \, A\, ). Thus, the matrix norm is a function \, \cdot\, : K^ \to \R that must satisfy the following properties: For all scalars \alpha \in K and matrices A, B \in K^, *\, A\, \ge 0 (''positive-valued'') *\, A\, = 0 \iff A=0_ (''definite'') *\left\, \alpha A\right\, =\left, \alpha\ \left\, A\right\, (''absolutely homogeneous'') *\, A+B\, \le \, A\, +\, B\, (''sub-additive'' or satisfying the ''triangle inequality'') The only feature distinguishing matrices from rearranged vectors is multiplication. Matrix norms are particularly useful if they are also sub-multiplicative: *\left\, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Operator Norm
In mathematics, the operator norm measures the "size" of certain linear operators by assigning each a real number called its . Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces. Introduction and definition Given two normed vector spaces V and W (over the same base field, either the real numbers \R or the complex numbers \Complex), a linear map A : V \to W is continuous if and only if there exists a real number c such that \, Av\, \leq c \, v\, \quad \mbox v\in V. The norm on the left is the one in W and the norm on the right is the one in V. Intuitively, the continuous operator A never increases the length of any vector by more than a factor of c. Thus the image of a bounded set under a continuous operator is also bounded. Because of this property, the continuous linear operators are also known as bounded operators. In order to "measure the size" of A, one can take the infimum of the numbers c such that the above i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isometry
In mathematics, an isometry (or congruence, or congruent transformation) is a distance-preserving transformation between metric spaces, usually assumed to be bijective. The word isometry is derived from the Ancient Greek: ἴσος ''isos'' meaning "equal", and μέτρον ''metron'' meaning "measure". Introduction Given a metric space (loosely, a set and a scheme for assigning distances between elements of the set), an isometry is a transformation which maps elements to the same or another metric space such that the distance between the image elements in the new metric space is equal to the distance between the elements in the original metric space. In a two-dimensional or three-dimensional Euclidean space, two geometric figures are congruent if they are related by an isometry; the isometry that relates them is either a rigid motion (translation or rotation), or a composition of a rigid motion and a reflection. Isometries are often used in constructions where one space i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Norm
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any positive integer dimension, including the three-dimensional space and the '' Euclidean plane'' (dimension two). The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics. Ancient Greek geometers introduced Euclidean space for modeling the physical space. Their work was collected by the ancient Greek mathematician Euclid in his ''Elements'', with the great innovation of '' proving'' all properties of the space as theorems, by starting from a few fundamental properties, called ''postulates'', which either were considered as evident (for example, there is exactly one straight line passing through two points), or seemed impossible to prove (par ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adjoint Filter
In signal processing, the adjoint filter mask h^* of a filter mask h is reversed in time and the elements are complex conjugated. :(h^*)_k = \overline Its name is derived from the fact that the convolution with the adjoint filter is the adjoint operator of the original filter, with respect to the Hilbert space \ell_2 of the sequences in which the inner product is the Euclidean norm. :\langle h*x, y \rangle = \langle x, h^* * y \rangle The autocorrelation Autocorrelation, sometimes known as serial correlation in the discrete time case, is the correlation of a signal with a delayed copy of itself as a function of delay. Informally, it is the similarity between observations of a random variable ... of a signal x can be written as x^* * x. Properties * ^* = h * (h*g)^* = h^* * g^* * (h\leftarrow k)^* = h^* \rightarrow k References Digital signal processing {{signal-processing-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transposed Matrix
In linear algebra, the transpose of a matrix is an operator which flips a matrix over its diagonal; that is, it switches the row and column indices of the matrix by producing another matrix, often denoted by (among other notations). The transpose of a matrix was introduced in 1858 by the British mathematician Arthur Cayley. In the case of a logical matrix representing a binary relation R, the transpose corresponds to the converse relation RT. Transpose of a matrix Definition The transpose of a matrix , denoted by , , , A^, , , or , may be constructed by any one of the following methods: # Reflect over its main diagonal (which runs from top-left to bottom-right) to obtain #Write the rows of as the columns of #Write the columns of as the rows of Formally, the -th row, -th column element of is the -th row, -th column element of : :\left mathbf^\operatorname\right = \left mathbf\right. If is an matrix, then is an matrix. In the case of square matrices, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
