|
Place Value
Positional notation (or place-value notation, or positional numeral system) usually denotes the extension to any base of the Hindu–Arabic numeral system (or decimal system). More generally, a positional system is a numeral system in which the contribution of a digit to the value of a number is the value of the digit multiplied by a factor determined by the position of the digit. In early numeral systems, such as Roman numerals, a digit has only one value: I means one, X means ten and C a hundred (however, the value may be negated if placed before another digit). In modern positional systems, such as the decimal system, the position of the digit means that its value must be multiplied by some value: in 555, the three identical symbols represent five hundreds, five tens, and five units, respectively, due to their different positions in the digit string. The Babylonian numeral system, base 60, was the first positional system to be developed, and its influence is present today ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positional Notation Glossary-en
Positional notation (or place-value notation, or positional numeral system) usually denotes the extension to any base of the Hindu–Arabic numeral system (or decimal system). More generally, a positional system is a numeral system in which the contribution of a digit to the value of a number is the value of the digit multiplied by a factor determined by the position of the digit. In early numeral systems, such as Roman numerals, a digit has only one value: I means one, X means ten and C a hundred (however, the value may be negated if placed before another digit). In modern positional systems, such as the decimal system, the position of the digit means that its value must be multiplied by some value: in 555, the three identical symbols represent five hundreds, five tens, and five units, respectively, due to their different positions in the digit string. The Babylonian numeral system, base 60, was the first positional system to be developed, and its influence is present today ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
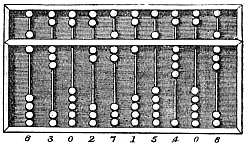
Abacus 6
The abacus (''plural'' abaci or abacuses), also called a counting frame, is a calculating tool which has been used since ancient times. It was used in the ancient Near East, Europe, China, and Russia, centuries before the adoption of the Hindu-Arabic numeral system. The exact origin of the abacus has not yet emerged. It consists of rows of movable beads, or similar objects, strung on a wire. They represent digits. One of the two numbers is set up, and the beads are manipulated to perform an operation such as addition, or even a square or cubic root. In their earliest designs, the rows of beads could be loose on a flat surface or sliding in grooves. Later the beads were made to slide on rods and built into a frame, allowing faster manipulation. Abacuses are still made, often as a bamboo frame with beads sliding on wires. In the ancient world, particularly before the introduction of positional notation, abacuses were a practical calculating tool. The abacus is still used to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Counting Rods
Counting rods () are small bars, typically 3–14 cm long, that were used by mathematicians for calculation in ancient East Asia. They are placed either horizontally or vertically to represent any integer or rational number. The written forms based on them are called rod numerals. They are a true positional numeral system with digits for 1–9 and a blank for 0, from the Warring states period (circa 475 BCE) to the 16th century. History Chinese arithmeticians used counting rods well over two thousand years ago. In 1954 forty-odd counting rods of the Warring States period (5th century BCE to 221 BCE) were found in Zuǒjiāgōngshān (左家公山) Chu (state), Chu Grave No.15 in Changsha, Hunan. In 1973 archeologists unearthed a number of wood scripts from a tomb in Hubei dating from the period of the Han dynasty (206 BCE to 220 CE). On one of the wooden scripts was written: "当利二月定算𝍥". This is one of the earliest examples of using counting-rod nu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abacus
The abacus (''plural'' abaci or abacuses), also called a counting frame, is a calculating tool which has been used since ancient times. It was used in the ancient Near East, Europe, China, and Russia, centuries before the adoption of the Hindu-Arabic numeral system. The exact origin of the abacus has not yet emerged. It consists of rows of movable beads, or similar objects, strung on a wire. They represent digits. One of the two numbers is set up, and the beads are manipulated to perform an operation such as addition, or even a square or cubic root. In their earliest designs, the rows of beads could be loose on a flat surface or sliding in grooves. Later the beads were made to slide on rods and built into a frame, allowing faster manipulation. Abacuses are still made, often as a bamboo frame with beads sliding on wires. In the ancient world, particularly before the introduction of positional notation, abacuses were a practical calculating tool. The abacus is still used to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sign-value Notation
A sign-value notation represents numbers by a series of numeric signs that added together equal the number represented. In Roman numerals for example, X means ten and L means fifty. Hence LXXX means eighty (50 + 10 + 10 + 10). There is no need for zero in sign-value notation. History Sign-value notation was the ancient way of writing numbers and only gradually evolved into place-value notation, also known as positional notation. When ancient people wanted to write "two sheep" in clay, they could inscribe in clay a picture of two sheep. But this would be impractical when they wanted to write "twenty sheep". In Mesopotamia they used small clay tokens to represent a number of a specific commodity, and strung the tokens like beads on a string, which were used for accounting. There was a token for one sheep and a token for ten sheep, and a different token for ten goats, etc. To ensure that nobody could alter the number and type of tokens, they inven ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Karl Menninger (mathematics)
Karl Menninger (October 6, 1898 – October 2, 1963) was a German teacher of and writer about mathematics. His major work was ''Zahlwort und Ziffer'' (1934,; English trans., ''Number Words and Number Symbols''), about non-academic mathematics in much of the world. (The omission of Africa was rectified by Claudia Zaslavsky Claudia Zaslavsky (January 12, 1917 – January 13, 2006) was an American mathematics teacher and ethnomathematician. Life She was born Claudia Natoma Cohen (later changed to Cogan) on January 12, 1917, in Upper Manhattan in New York City an ... in her book ''Africa Counts''.) References *Dauben, Joseph Warren, and Christoph Scriba, eds. (2002), ''Writing the History of Mathematics'', Birkhäuser, Basel, page 483. *Menninger, Karl (1934), ''Zahlwort und Ziffer''. Revised edition (1958). Göttingen: Vandenhoeck and Ruprecht. *Menninger, Karl (1969), ''Number Words and Number Symbols''. Cambridge, Mass.: The M.I.T. Press. German historians of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Carl Friedrich Gauss
Johann Carl Friedrich Gauss (; german: Gauß ; la, Carolus Fridericus Gauss; 30 April 177723 February 1855) was a German mathematician and physicist who made significant contributions to many fields in mathematics and science. Sometimes referred to as the ''Princeps mathematicorum'' () and "the greatest mathematician since antiquity", Gauss had an exceptional influence in many fields of mathematics and science, and he is ranked among history's most influential mathematicians. Also available at Retrieved 23 February 2014. Comprehensive biographical article. Biography Early years Johann Carl Friedrich Gauss was born on 30 April 1777 in Brunswick (Braunschweig), in the Duchy of Brunswick-Wolfenbüttel (now part of Lower Saxony, Germany), to poor, working-class parents. His mother was illiterate and never recorded the date of his birth, remembering only that he had been born on a Wednesday, eight days before the Feast of the Ascension (which occurs 39 days after Easter). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Sand Reckoner
''The Sand Reckoner'' ( el, Ψαμμίτης, ''Psammites'') is a work by Archimedes, an Ancient Greek mathematician of the 3rd century BC, in which he set out to determine an upper bound for the number of grains of sand that fit into the universe. In order to do this, he had to estimate the size of the universe according to the contemporary model, and invent a way to talk about extremely large numbers. The work, also known in Latin as ''Archimedis Syracusani Arenarius & Dimensio Circuli'', which is about eight pages long in translation, is addressed to the Syracusan king Gelo II (son of Hiero II), and is probably the most accessible work of Archimedes; in some sense, it is the first research-expository paper.Archimedes, The Sand Reckoner 511 R U, by Ilan Vardi accessed 28-II-2007. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archimedes
Archimedes of Syracuse (;; ) was a Greek mathematician, physicist, engineer, astronomer, and inventor from the ancient city of Syracuse in Sicily. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Considered the greatest mathematician of ancient history, and one of the greatest of all time,* * * * * * * * * * Archimedes anticipated modern calculus and analysis by applying the concept of the infinitely small and the method of exhaustion to derive and rigorously prove a range of geometrical theorems. These include the area of a circle, the surface area and volume of a sphere, the area of an ellipse, the area under a parabola, the volume of a segment of a paraboloid of revolution, the volume of a segment of a hyperboloid of revolution, and the area of a spiral. Heath, Thomas L. 1897. ''Works of Archimedes''. Archimedes' other mathematical achievements include deriving an approximation of pi, de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variable (mathematics)
In mathematics, a variable (from Latin '' variabilis'', "changeable") is a symbol that represents a mathematical object. A variable may represent a number, a vector, a matrix, a function, the argument of a function, a set, or an element of a set. Algebraic computations with variables as if they were explicit numbers solve a range of problems in a single computation. For example, the quadratic formula solves any quadratic equation by substituting the numeric values of the coefficients of that equation for the variables that represent them in the quadratic formula. In mathematical logic, a ''variable'' is either a symbol representing an unspecified term of the theory (a meta-variable), or a basic object of the theory that is manipulated without referring to its possible intuitive interpretation. History In ancient works such as Euclid's ''Elements'', single letters refer to geometric points and shapes. In the 7th century, Brahmagupta used different colours to represe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zero
0 (zero) is a number representing an empty quantity. In place-value notation such as the Hindu–Arabic numeral system, 0 also serves as a placeholder numerical digit, which works by multiplying digits to the left of 0 by the radix, usually by 10. As a number, 0 fulfills a central role in mathematics as the additive identity of the integers, real numbers, and other algebraic structures. Common names for the number 0 in English are ''zero'', ''nought'', ''naught'' (), ''nil''. In contexts where at least one adjacent digit distinguishes it from the letter O, the number is sometimes pronounced as ''oh'' or ''o'' (). Informal or slang terms for 0 include ''zilch'' and ''zip''. Historically, ''ought'', ''aught'' (), and ''cipher'', have also been used. Etymology The word ''zero'' came into the English language via French from the Italian , a contraction of the Venetian form of Italian via ''ṣafira'' or ''ṣifr''. In pre-Islamic time the word (Arabic ) had the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |




_by_Thomas_Degeorge.png)