|
Perturbation Series
In mathematics and applied mathematics, perturbation theory comprises methods for finding an approximate solution to a problem, by starting from the exact solution of a related, simpler problem. A critical feature of the technique is a middle step that breaks the problem into "solvable" and "perturbative" parts. In perturbation theory, the solution is expressed as a power series in a small parameter The first term is the known solution to the solvable problem. Successive terms in the series at higher powers of \varepsilon usually become smaller. An approximate 'perturbation solution' is obtained by truncating the series, usually by keeping only the first two terms, the solution to the known problem and the 'first order' perturbation correction. Perturbation theory is used in a wide range of fields, and reaches its most sophisticated and advanced forms in quantum field theory. Perturbation theory (quantum mechanics) describes the use of this method in quantum mechanics. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
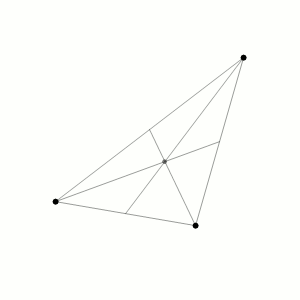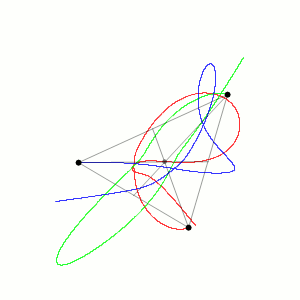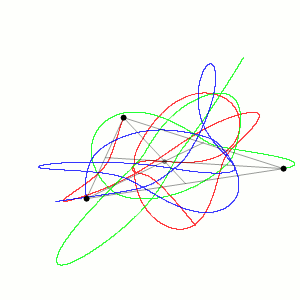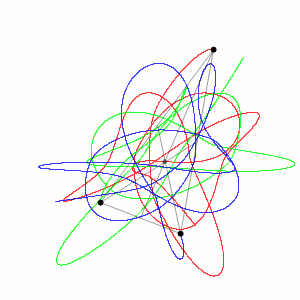
Three-body Problem
In physics and classical mechanics, the three-body problem is the problem of taking the initial positions and velocities (or momenta) of three point masses and solving for their subsequent motion according to Newton's laws of motion and Newton's law of universal gravitation. The three-body problem is a special case of the n-body problem, -body problem. Unlike two-body problems, no general closed-form solution exists, as the resulting dynamical system is chaos theory, chaotic for most initial conditions, and numerical methods are generally required. Historically, the first specific three-body problem to receive extended study was the one involving the Moon, Earth, and the Sun. In an extended modern sense, a three-body problem is any problem in classical mechanics Classical mechanics is a physical theory describing the motion of macroscopic objects, from projectiles to parts of machinery, and astronomical objects, such as spacecraft, planets, stars, and galaxies. For o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trajectory
A trajectory or flight path is the path that an object with mass in motion follows through space as a function of time. In classical mechanics, a trajectory is defined by Hamiltonian mechanics via canonical coordinates; hence, a complete trajectory is defined by position and momentum, simultaneously. The mass might be a projectile or a satellite. For example, it can be an orbit — the path of a planet, asteroid, or comet as it travels around a central mass. In control theory, a trajectory is a time-ordered set of states of a dynamical system (see e.g. Poincaré map). In discrete mathematics, a trajectory is a sequence (f^k(x))_ of values calculated by the iterated application of a mapping f to an element x of its source. Physics of trajectories A familiar example of a trajectory is the path of a projectile, such as a thrown ball or rock. In a significantly simplified model, the object moves only under the influence of a uniform gravitational force field. This can be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamiltonian (quantum Mechanics)
Hamiltonian may refer to: * Hamiltonian mechanics, a function that represents the total energy of a system * Hamiltonian (quantum mechanics), an operator corresponding to the total energy of that system ** Dyall Hamiltonian, a modified Hamiltonian with two-electron nature ** Molecular Hamiltonian, the Hamiltonian operator representing the energy of the electrons and nuclei in a molecule * Hamiltonian (control theory), a function used to solve a problem of optimal control for a dynamical system * Hamiltonian path, a path in a graph that visits each vertex exactly once * Hamiltonian group, a non-abelian group the subgroups of which are all normal * Hamiltonian economic program, the economic policies advocated by Alexander Hamilton, the first United States Secretary of the Treasury See also * Alexander Hamilton (1755 or 1757–1804), American statesman and one of the Founding Fathers of the US * Hamilton (other) Hamilton may refer to: People * Hamilton (name), a common ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Mechanics
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. It does not assume or postulate any natural laws, but explains the macroscopic behavior of nature from the behavior of such ensembles. Statistical mechanics arose out of the development of classical thermodynamics, a field for which it was successful in explaining macroscopic physical properties—such as temperature, pressure, and heat capacity—in terms of microscopic parameters that fluctuate about average values and are characterized by probability distributions. This established the fields of statistical thermodynamics and statistical physics. The founding of the field of statistical mechanics is generally credited to three physicists: *Ludwig Boltzmann, who developed the fundamental interpretation of entropy in terms of a collection of microstates *James Clerk Maxwell, who developed models of probability distr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamic Free Energy
The thermodynamic free energy is a concept useful in the thermodynamics of chemical or thermal processes in engineering and science. The change in the free energy is the maximum amount of work that a thermodynamic system can perform in a process at constant temperature, and its sign indicates whether the process is thermodynamically favorable or forbidden. Since free energy usually contains potential energy, it is not absolute but depends on the choice of a zero point. Therefore, only relative free energy values, or changes in free energy, are physically meaningful. The free energy is a thermodynamic state function, like the internal energy, enthalpy, and entropy. The free energy is the portion of any first-law energy that is available to perform thermodynamic work at constant temperature, ''i.e.'', work mediated by thermal energy. Free energy is subject to irreversible loss in the course of such work. Since first-law energy is always conserved, it is evident that free energy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave Equation
The (two-way) wave equation is a second-order linear partial differential equation for the description of waves or standing wave fields — as they occur in classical physics — such as mechanical waves (e.g. water waves, sound waves and seismic waves) or electromagnetic waves (including light waves). It arises in fields like acoustics, electromagnetism, and fluid dynamics. Single mechanical or electromagnetic waves propagating in a pre-defined direction can also be described with the first-order one-way wave equation which is much easier to solve and also valid for inhomogenious media. Introduction The (two-way) wave equation is a second-order partial differential equation describing waves, including traveling and standing waves; the latter can be considered as linear superpositions of waves traveling in opposite directions. This article mostly focuses on the scalar wave equation describing waves in scalars by scalar functions of a time variable (a variable repres ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equations Of Motion
In physics, equations of motion are equations that describe the behavior of a physical system in terms of its motion as a function of time.''Encyclopaedia of Physics'' (second Edition), R.G. Lerner, G.L. Trigg, VHC Publishers, 1991, ISBN (Verlagsgesellschaft) 3-527-26954-1 (VHC Inc.) 0-89573-752-3 More specifically, the equations of motion describe the behavior of a physical system as a set of mathematical functions in terms of dynamic variables. These variables are usually spatial coordinates and time, but may include momentum components. The most general choice are generalized coordinates which can be any convenient variables characteristic of the physical system.''Analytical Mechanics'', L.N. Hand, J.D. Finch, Cambridge University Press, 2008, The functions are defined in a Euclidean space in classical mechanics, but are replaced by curved spaces in relativity. If the dynamics of a system is known, the equations are the solutions for the differential equations describi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Equation
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, and the differential equation defines a relationship between the two. Such relations are common; therefore, differential equations play a prominent role in many disciplines including engineering, physics, economics, and biology. Mainly the study of differential equations consists of the study of their solutions (the set of functions that satisfy each equation), and of the properties of their solutions. Only the simplest differential equations are solvable by explicit formulas; however, many properties of solutions of a given differential equation may be determined without computing them exactly. Often when a closed-form expression for the solutions is not available, solutions may be approximated numerically using computers. The theory of d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Equation
In mathematics, an algebraic equation or polynomial equation is an equation of the form :P = 0 where ''P'' is a polynomial with coefficients in some field, often the field of the rational numbers. For many authors, the term ''algebraic equation'' refers only to ''univariate equations'', that is polynomial equations that involve only one variable. On the other hand, a polynomial equation may involve several variables. In the case of several variables (the ''multivariate'' case), the term ''polynomial equation'' is usually preferred to ''algebraic equation''. For example, :x^5-3x+1=0 is an algebraic equation with integer coefficients and :y^4 + \frac - \frac + xy^2 + y^2 + \frac = 0 is a multivariate polynomial equation over the rationals. Some but not all polynomial equations with rational coefficients have a solution that is an algebraic expression that can be found using a finite number of operations that involve only those same types of coefficients (that is, can be solved alg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Feynman Diagram
In theoretical physics, a Feynman diagram is a pictorial representation of the mathematical expressions describing the behavior and interaction of subatomic particles. The scheme is named after American physicist Richard Feynman, who introduced the diagrams in 1948. The interaction of subatomic particles can be complex and difficult to understand; Feynman diagrams give a simple visualization of what would otherwise be an arcane and abstract formula. According to David Kaiser, "Since the middle of the 20th century, theoretical physicists have increasingly turned to this tool to help them undertake critical calculations. Feynman diagrams have revolutionized nearly every aspect of theoretical physics." While the diagrams are applied primarily to quantum field theory, they can also be used in other fields, such as solid-state theory. Frank Wilczek wrote that the calculations that won him the 2004 Nobel Prize in Physics "would have been literally unthinkable without Feynman diagra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oxford University Press
Oxford University Press (OUP) is the university press of the University of Oxford. It is the largest university press in the world, and its printing history dates back to the 1480s. Having been officially granted the legal right to print books by decree in 1586, it is the second oldest university press after Cambridge University Press. It is a department of the University of Oxford and is governed by a group of 15 academics known as the Delegates of the Press, who are appointed by the vice-chancellor of the University of Oxford. The Delegates of the Press are led by the Secretary to the Delegates, who serves as OUP's chief executive and as its major representative on other university bodies. Oxford University Press has had a similar governance structure since the 17th century. The press is located on Walton Street, Oxford, opposite Somerville College, in the inner suburb of Jericho. For the last 500 years, OUP has primarily focused on the publication of pedagogical texts and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |




.jpg)