|
Perturbation Function
In mathematical optimization, the perturbation function is any function which relates to primal and dual problems. The name comes from the fact that any such function defines a perturbation of the initial problem. In many cases this takes the form of shifting the constraints. In some texts the value function is called the perturbation function, and the perturbation function is called the bifunction. Definition Given two dual pairs of separated locally convex spaces \left(X,X^*\right) and \left(Y,Y^*\right). Then given the function f: X \to \mathbb \cup \, we can define the primal problem by :\inf_ f(x). \, If there are constraint conditions, these can be built into the function f by letting f \leftarrow f + I_\mathrm where I is the characteristic function. Then F: X \times Y \to \mathbb \cup \ is a ''perturbation function'' if and only if F(x,0) = f(x). Use in duality The duality gap is the difference of the right and left hand side of the inequality :\sup_ -F^*(0,y^*) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems of sorts arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries. In the more general approach, an optimization problem consists of maxima and minima, maximizing or minimizing a Function of a real variable, real function by systematically choosing Argument of a function, input values from within an allowed set and computing the Value (mathematics), value of the function. The generalization of optimization theory and techniques to other formulations constitutes a large area of applied mathematics. More generally, opti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proper Convex Function
In mathematical analysis, in particular the subfields of convex analysis and optimization, a proper convex function is an extended real-valued convex function with a non-empty domain, that never takes on the value -\infty and also is not identically equal to +\infty. In convex analysis and variational analysis, a point (in the domain) at which some given function f is minimized is typically sought, where f is valued in the extended real number line \infty, \infty= \mathbb \cup \. Such a point, if it exists, is called a of the function and its value at this point is called the () of the function. If the function takes -\infty as a value then -\infty is necessarily the global minimum value and the minimization problem can be answered; this is ultimately the reason why the definition of "" requires that the function never take -\infty as a value. Assuming this, if the function's domain is empty or if the function is identically equal to +\infty then the minimization problem once a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fenchel Duality
In mathematics, Fenchel's duality theorem is a result in the theory of convex functions named after Werner Fenchel. Let ''ƒ'' be a proper convex function on R''n'' and let ''g'' be a proper concave function on R''n''. Then, if regularity conditions are satisfied, :\inf_x ( f(x)-g(x) ) = \sup_p ( g_*(p)-f^*(p)). where ''ƒ'' * is the convex conjugate of ''ƒ'' (also referred to as the Fenchel–Legendre transform) and ''g'' * is the concave conjugate of ''g''. That is, :f^ \left( x^ \right) := \sup \left \ :g_ \left( x^ \right) := \inf \left \ Mathematical theorem Let ''X'' and ''Y'' be Banach spaces, f: X \to \mathbb \cup \ and g: Y \to \mathbb \cup \ be convex functions and A: X \to Y be a bounded linear map. Then the Fenchel problems: :p^* = \inf_ \ :d^* = \sup_ \ satisfy weak duality, i.e. p^* \geq d^*. Note that f^*,g^* are the convex conjugates of ''f'',''g'' respectively, and A^* is the adjoint operator. The perturbation function for th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
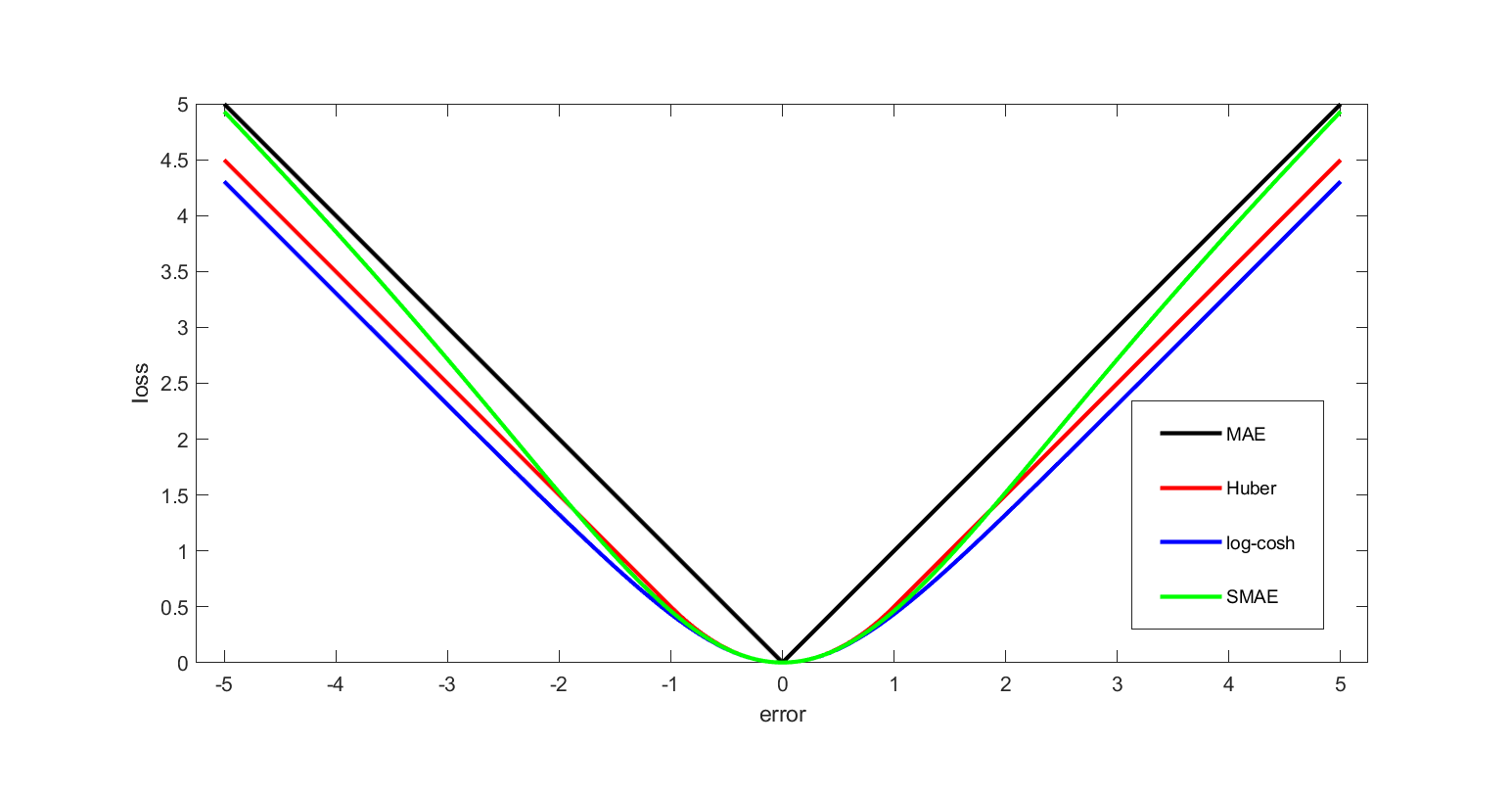
Objective Function
In mathematical optimization and decision theory, a loss function or cost function (sometimes also called an error function) is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost" associated with the event. An optimization problem seeks to minimize a loss function. An objective function is either a loss function or its opposite (in specific domains, variously called a reward function, a profit function, a utility function, a fitness function, etc.), in which case it is to be maximized. The loss function could include terms from several levels of the hierarchy. In statistics, typically a loss function is used for parameter estimation, and the event in question is some function of the difference between estimated and true values for an instance of data. The concept, as old as Laplace, was reintroduced in statistics by Abraham Wald in the middle of the 20th century. In the context of economics, for example, this ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adjoint Operator
In mathematics, specifically in operator theory, each linear operator A on a Euclidean vector space defines a Hermitian adjoint (or adjoint) operator A^* on that space according to the rule :\langle Ax,y \rangle = \langle x,A^*y \rangle, where \langle \cdot,\cdot \rangle is the inner product on the vector space. The adjoint may also be called the Hermitian conjugate or simply the Hermitian after Charles Hermite. It is often denoted by in fields like physics, especially when used in conjunction with bra–ket notation in quantum mechanics. In finite dimensions where operators are represented by matrices, the Hermitian adjoint is given by the conjugate transpose (also known as the Hermitian transpose). The above definition of an adjoint operator extends verbatim to bounded linear operators on Hilbert spaces H. The definition has been further extended to include unbounded '' densely defined'' operators whose domain is topologically dense in—but not necessarily equal to—H. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Map
In mathematics, and more specifically in linear algebra, a linear map (also called a linear mapping, linear transformation, vector space homomorphism, or in some contexts linear function) is a Map (mathematics), mapping V \to W between two vector spaces that preserves the operations of vector addition and scalar multiplication. The same names and the same definition are also used for the more general case of module (mathematics), modules over a ring (mathematics), ring; see Module homomorphism. If a linear map is a bijection then it is called a . In the case where V = W, a linear map is called a (linear) ''endomorphism''. Sometimes the term refers to this case, but the term "linear operator" can have different meanings for different conventions: for example, it can be used to emphasize that V and W are Real number, real vector spaces (not necessarily with V = W), or it can be used to emphasize that V is a function space, which is a common convention in functional analysis. Some ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fréchet Space
In functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces (normed vector spaces that are complete with respect to the metric induced by the norm). All Banach and Hilbert spaces are Fréchet spaces. Spaces of infinitely differentiable functions are typical examples of Fréchet spaces, many of which are typically Banach spaces. A Fréchet space X is defined to be a locally convex metrizable topological vector space (TVS) that is complete as a TVS, meaning that every Cauchy sequence in X converges to some point in X (see footnote for more details).Here "Cauchy" means Cauchy with respect to the canonical uniformity that every TVS possess. That is, a sequence x_ = \left(x_m\right)_^ in a TVS X is Cauchy if and only if for all neighborhoods U of the origin in X, x_m - x_n \in U whenever m and n are sufficiently large. Note that this definition of a Cau ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projection (set Theory)
In set theory, a projection is one of two closely related types of functions or operations, namely: * A set-theoretic operation typified by the ''j''th projection map, written \mathrm_, that takes an element \vec = (x_1,\ \ldots,\ x_j,\ \ldots,\ x_k) of the Cartesian product (X_1 \times \cdots \times X_j \times \cdots \times X_k) to the value \mathrm_(\vec) = x_j. * A function that sends an element ''x'' to its equivalence class under a specified equivalence relation ''E'', or, equivalently, a surjection from a set to another set.. The function from elements to equivalence classes is a surjection, and every surjection corresponds to an equivalence relation under which two elements are equivalent when they have the same image. The result of the mapping is written as 'x''when ''E'' is understood, or written as 'x''sub>''E'' when it is necessary to make ''E'' explicit. See also * Cartesian product * Projection (relational algebra) * Projection (mathematics) * Relation Relation or re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Interior
In functional analysis, a branch of mathematics, the algebraic interior or radial kernel of a subset of a vector space is a refinement of the concept of the interior. Definition Assume that A is a subset of a vector space X. The ''algebraic interior'' (or ''radial kernel'') ''of A with respect to X'' is the set of all points at which A is a radial set. A point a_0 \in A is called an of A and A is said to be if for every x \in X there exists a real number t_x > 0 such that for every t \in , t_x a_0 + t x \in A. This last condition can also be written as a_0 + , t_xx \subseteq A where the set a_0 + , t_xx ~:=~ \left\ is the line segment (or closed interval) starting at a_0 and ending at a_0 + t_x x; this line segment is a subset of a_0 + radial points of the set. If M is a linear subspace of X and A \subseteq X then this definition can be generalized to the ''algebraic interior of A with respect to M'' is: \operatorname_M A := \left\. where \operatorname_M A \subseteq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lower Semi-continuous
In mathematical analysis, semicontinuity (or semi-continuity) is a property of extended real-valued functions that is weaker than continuity. An extended real-valued function f is upper (respectively, lower) semicontinuous at a point x_0 if, roughly speaking, the function values for arguments near x_0 are not much higher (respectively, lower) than f\left(x_0\right). A function is continuous if and only if it is both upper and lower semicontinuous. If we take a continuous function and increase its value at a certain point x_0 to f\left(x_0\right) + c for some c>0, then the result is upper semicontinuous; if we decrease its value to f\left(x_0\right) - c then the result is lower semicontinuous. The notion of upper and lower semicontinuous function was first introduced and studied by René Baire in his thesis in 1899. Definitions Assume throughout that X is a topological space and f:X\to\overline is a function with values in the extended real numbers \overline=\R \cup \ = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Function
In mathematics, a real-valued function is called convex if the line segment between any two points on the graph of a function, graph of the function lies above the graph between the two points. Equivalently, a function is convex if its epigraph (mathematics), epigraph (the set of points on or above the graph of the function) is a convex set. A twice-differentiable function of a single variable is convex if and only if its second derivative is nonnegative on its entire domain. Well-known examples of convex functions of a single variable include the quadratic function x^2 and the exponential function e^x. In simple terms, a convex function refers to a function whose graph is shaped like a cup \cup, while a concave function's graph is shaped like a cap \cap. Convex functions play an important role in many areas of mathematics. They are especially important in the study of optimization problems where they are distinguished by a number of convenient properties. For instance, a st ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strong Duality
Strong duality is a condition in mathematical optimization in which the primal optimal objective and the dual optimal objective are equal. This is as opposed to weak duality (the primal problem has optimal value smaller than or equal to the dual problem, in other words the duality gap is greater than or equal to zero). Characterizations Strong duality holds if and only if the duality gap is equal to 0. Sufficient conditions Sufficient conditions comprise: * F = F^ where F is the perturbation function relating the primal and dual problems and F^ is the biconjugate of F (follows by construction of the duality gap) * F is convex and lower semi-continuous (equivalent to the first point by the Fenchel–Moreau theorem) * the primal problem is a linear optimization problem * Slater's condition for a convex optimization problem See also *Convex optimization Convex optimization is a subfield of mathematical optimization that studies the problem of minimizing convex function ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
