|
Puzzle-solving
A puzzle is a game, problem, or toy that tests a person's ingenuity or knowledge. In a puzzle, the solver is expected to put pieces together ( or take them apart) in a logical way, in order to arrive at the correct or fun solution of the puzzle. There are different genres of puzzles, such as crossword puzzles, word-search puzzles, number puzzles, relational puzzles, and logic puzzles. The academic study of puzzles is called enigmatology. Puzzles are often created to be a form of entertainment but they can also arise from serious mathematical or logical problems. In such cases, their solution may be a significant contribution to mathematical research. Etymology The ''Oxford English Dictionary'' dates the word ''puzzle'' (as a verb) to the end of the 16th century. Its earliest use documented in the ''OED'' was in a book titled ''The Voyage of Robert Dudley...to the West Indies, 1594–95, narrated by Capt. Wyatt, by himself, and by Abram Kendall, master'' (published circa 1595) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Game
A game is a structured form of play (activity), play, usually undertaken for enjoyment, entertainment or fun, and sometimes used as an educational tool. Many games are also considered to be work (such as professional players of spectator sports or games) or art (such as jigsaw puzzles or games involving an artistic layout such as Mahjong, solitaire, or some video games). Games are sometimes played purely for enjoyment, sometimes for achievement or reward as well. They can be played alone, in teams, or online; by amateurs or by professionals. The players may have an audience of non-players, such as when people are entertained by watching a World Chess Championship, chess championship. On the other hand, players in a game may constitute their own audience as they take their turn to play. Often, part of the entertainment for children playing a game is deciding who is part of their audience and who is a player. A toy and a game are not the same. Toys generally allow for unrestr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Puzzle
Mathematical puzzles make up an integral part of recreational mathematics. They have specific rules, but they do not usually involve competition between two or more players. Instead, to solve such a puzzle, the solver must find a solution that satisfies the given conditions. Mathematical puzzles require mathematics to solve them. Logic puzzles are a common type of mathematical puzzle. Conway's Game of Life and fractals, as two examples, may also be considered mathematical puzzles even though the solver interacts with them only at the beginning by providing a set of initial conditions. After these conditions are set, the rules of the puzzle determine all subsequent changes and moves. Many of the puzzles are well known because they were discussed by Martin Gardner in his "Mathematical Games" column in Scientific American. Mathematical puzzles are sometimes used to motivate students in teaching elementary school math problem solving techniques.Kulkarni, DEnjoying Math: Learning Problem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Peg Solitaire
Peg solitaire, Solo Noble or simply Solitaire is a board game for one player involving movement of pegs on a board with holes. Some sets use marbles in a board with indentations. The game is known as solitaire in Britain and as peg solitaire in the US where 'solitaire' is now the common name for patience. It is also called Brainvita in India, where sets are sold commercially under this name. The first evidence of the game can be traced back to the court of Louis XIV, and the specific date of 1697, with an engraving made ten years later by Claude Auguste Berey of Anne de Rohan-Chabot, Princess of Soubise, with the puzzle by her side. The August 1697 edition of the French literary magazine '' Mercure galant'' contains a description of the board, rules and sample problems. This is the first known reference to the game in print. The standard game fills the entire board with pegs except for the central hole. The objective is, making valid moves, to empty the entire board except fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Combination Puzzle
A combination puzzle, also known as a sequential move puzzle, is a puzzle which consists of a set of pieces which can be manipulated into different combinations by a group of operations. Many such puzzles are mechanical puzzles of polyhedral shape, consisting of multiple layers of pieces along each axis which can rotate independently of each other. Collectively known as twisty puzzles, the archetype of this kind of puzzle is the Rubik's Cube. Each rotating side is usually marked with different colours, intended to be scrambled, then 'solved' by a sequence of moves that sort the facets by colour. As a generalisation, combination puzzles also include mathematically defined examples that have not been, or are impossible to, physically construct. Description A combination puzzle is solved by achieving a particular combination starting from a random (scrambled) combination. Often, the solution is required to be some recognisable pattern such as "all like colours together" or "all ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Soma Cube
The Soma cube is a solid dissection puzzle invented by Danish polymath Piet Hein in 1933 during a lecture on quantum mechanics conducted by Werner Heisenberg. Seven pieces made out of unit cubes must be assembled into a 3×3×3 cube. The pieces can also be used to make a variety of other 3D shapes. The pieces of the Soma cube consist of all possible combinations of three or four unit cubes, joined at their faces, such that at least one inside corner is formed. There is one combination of three cubes that satisfies this condition, and six combinations of four cubes that satisfy this condition, of which two are mirror images of each other (see Chirality). Thus, 3 + (6 × 4) is 27, which is exactly the number of cells in a 3×3×3 cube. The Soma cube was popularized by Martin Gardner in the September 1958 Mathematical Games column in ''Scientific American.'' The book '' Winning Ways for your Mathematical Plays'' also contains a detailed analysis of the Soma cube problem. Ther ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rubik's Cube
The Rubik's Cube is a Three-dimensional space, 3-D combination puzzle originally invented in 1974 by Hungarians, Hungarian sculptor and professor of architecture Ernő Rubik. Originally called the Magic Cube, the puzzle was licensed by Rubik to be sold by Pentangle Puzzles in the UK in 1978, and then by Ideal Toy Company, Ideal Toy Corp in 1980 via businessman Tibor Laczi and Seven Towns founder Tom Kremer. The cube was released internationally in 1980 and became one of the most recognized icons in popular culture. It won the 1980 Spiel des Jahres, German Game of the Year special award for Best Puzzle. , 350 million cubes had been sold worldwide, making it the world's bestselling puzzle game and bestselling toy. The Rubik's Cube was inducted into the US National Toy Hall of Fame in 2014. On the original classic Rubik's Cube, each of the six faces was covered by nine stickers, each of one of six solid colours: white, red, blue, orange, green, and yellow. Some later versions ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mechanical Puzzle
A mechanical puzzle is a puzzle presented as a set of mechanically interlinked pieces in which the solution is to manipulate the whole object or parts of it. While puzzles of this type have been in use by humanity as early as the 3rd century BC, one of the most well-known mechanical puzzles of modern day is the Rubik's Cube, invented by the Hungarian architect Ernő Rubik in 1974. The puzzles are typically designed for a single player, where the goal is for the player to see through the principle of the object, rather than accidentally coming up with the right solution through trial and error. With this in mind, they are often used as an intelligence test or in problem solving training. History The oldest known mechanical puzzle comes from Greece and appeared in the 3rd century BC. The game consists of a square divided into 14 parts, and the aim was to create different shapes from these pieces. This is not easy to do. (see Ostomachion loculus Archimedius) In Iran "puzzle-lo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eight Queens Puzzle
The eight queens puzzle is the problem of placing eight chess queens on an 8×8 chessboard so that no two queens threaten each other; thus, a solution requires that no two queens share the same row, column, or diagonal. There are 92 solutions. The problem was first posed in the mid-19th century. In the modern era, it is often used as an example problem for various computer programming techniques. The eight queens puzzle is a special case of the more general ''n'' queens problem of placing ''n'' non-attacking queens on an ''n''×''n'' chessboard. Solutions exist for all natural numbers ''n'' with the exception of ''n'' = 2 and ''n'' = 3. Although the exact number of solutions is only known for ''n'' ≤ 27, the asymptotic growth rate of the number of solutions is (0.143 ''n'')''n''. History Chess composer Max Bezzel published the eight queens puzzle in 1848. Franz Nauck published the first solutions in 1850.W. W. Rouse Ball (1960) "The Eight Queens Problem", in ''Mathema ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Knight's Tour
A knight's tour is a sequence of moves of a knight on a chessboard such that the knight visits every square exactly once. If the knight ends on a square that is one knight's move from the beginning square (so that it could tour the board again immediately, following the same path), the tour is closed (or re-entrant); otherwise, it is open. The knight's tour problem is the mathematical problem of finding a knight's tour. Creating a program to find a knight's tour is a common problem given to computer science students. Variations of the knight's tour problem involve chessboards of different sizes than the usual , as well as irregular (non-rectangular) boards. Theory The knight's tour problem is an instance of the more general Hamiltonian path problem in graph theory. The problem of finding a closed knight's tour is similarly an instance of the Hamiltonian cycle problem. Unlike the general Hamiltonian path problem, the knight's tour problem can be solved in linear time. Histor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chess Problem
A chess problem, also called a chess composition, is a puzzle set by the composer using chess pieces on a chess board, which presents the solver with a particular task. For instance, a position may be given with the instruction that White is to move first, and checkmate Black in two moves against any possible defence. A chess problem fundamentally differs from over-the-board play in that the latter involves a struggle between black and white, whereas the former involves a competition between the composer and the solver. Most positions which occur in a chess problem are 'unrealistic' in the sense that they are very unlikely to occur in over-the-board play. There is a good deal of specialized jargon used in connection with chess problems; see glossary of chess problems for a list. Definition The term "chess problem" is not sharply defined: there is no clear demarcation between chess compositions on the one hand and puzzles or tactical exercises on the other. In practice, however, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sangaku
Sangaku or San Gaku ( ja, 算額, lit=calculation tablet) are Japanese geometrical problems or theorems on wooden tablets which were placed as offerings at Shinto shrines or Buddhist temples during the Edo period by members of all social classes. History The Sangaku were painted in color on wooden tablets ( ema) and hung in the precincts of Buddhist temples and Shinto shrines as offerings to the kami and buddhas, as challenges to the congregants, or as displays of the solutions to questions. Many of these tablets were lost during the period of modernization that followed the Edo period, but around nine hundred are known to remain. Fujita Kagen (1765–1821), a Japanese mathematician of prominence, published the first collection of ''sangaku'' problems, his ''Shimpeki Sampo'' (Mathematical problems Suspended from the Temple) in 1790, and in 1806 a sequel, the ''Zoku Shimpeki Sampo''. During this period Japan applied strict regulations to commerce and foreign relations for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Three Utilities Problem
The classical mathematical puzzle known as the three utilities problem or sometimes water, gas and electricity asks for non-crossing connections to be drawn between three houses and three utility companies in the plane. When posing it in the early 20th century, Henry Dudeney wrote that it was already an old problem. It is an impossible puzzle: it is not possible to connect all nine lines without crossing. Versions of the problem on nonplanar surfaces such as a torus or Möbius strip, or that allow connections to pass through other houses or utilities, can be solved. This puzzle can be formalized as a problem in topological graph theory by asking whether the complete bipartite graph K_, with vertices representing the houses and utilities and edges representing their connections, has a graph embedding in the plane. The impossibility of the puzzle corresponds to the fact that K_ is not a planar graph. Multiple proofs of this impossibility are known, and form part of the proof of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |

.jpg)

.jpg)
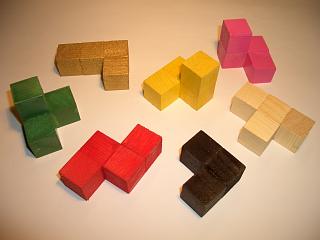



.png)
