|
Process Capability Index
The process capability index, or process capability ratio, is a statistical measure of process capability: the ability of an engineering process to produce an output within specification limits. The concept of process capability only holds meaning for processes that are in a state of statistical control. This means it cannot account for deviations which are not expected, such as misaligned, damaged, or worn equipment. Process capability indices measure how much "natural variation" a process experiences relative to its specification limits, and allows different processes to be compared to how well an organization controls them. Somewhat counterintuitively, higher index values indicate better performance, with zero indicating high deviation. Example for non-specialists A company produces axles with nominal diameter 20 mm on a lathe. As no axle can be made to ''exactly'' 20 mm, the designer specifies the maximum admissible deviations (called tolerances or specificatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Process Capability
The process capability is a measurable property of a Process (engineering), process to the specification, expressed as a process capability index (e.g., Cpk or Cpm) or as a process performance index (e.g., Ppk or Ppm). The output of this measurement is often illustrated by a histogram and calculations that predict how many parts will be produced out of specification (OOS). Two parts of process capability are: # Measure the variability of the output of a process, and # Compare that variability with a proposed specification or product tolerance Capabilities The input of a process usually has at least one or more measurable characteristics that are used to specify outputs. These can be analyzed statistically; where the output data shows a normal distribution the process can be described by the process mean (average) and the standard deviation. A process needs to be established with appropriate process controls in place. A control chart analysis is used to determine whether the p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Six Sigma
Six Sigma (6σ) is a set of techniques and tools for process improvement. It was introduced by American engineer Bill Smith while working at Motorola in 1986. Six Sigma strategies seek to improve manufacturing quality by identifying and removing the causes of defects and minimizing variability in manufacturing and business processes. This is done by using empirical and statistical quality management methods and by hiring people who serve as Six Sigma experts. Each Six Sigma project follows a defined methodology and has specific value targets, such as reducing pollution or increasing customer satisfaction. The term ''Six Sigma'' originates from statistical quality control, a reference to the fraction of a normal curve that lies within six standard deviations of the mean, used to represent a defect rate. History Motorola pioneered Six Sigma, setting a "six sigma" goal for its manufacturing business. It registered Six Sigma as a service mark on June 11, 1991 (); on December 28, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Process Performance Index
In process improvement efforts, the process performance index is an estimate of the process capability of a process during its initial set-up, ''before'' it has been brought into a state of statistical control. Formally, if the upper and lower specifications of the process are USL and LSL, the estimated mean of the process is \hat, and the estimated variability of the process (expressed as a standard deviation) is \hat, then the process performance index is defined as: :\hat_ = \min \Bigg , \Bigg/MATH> \hat is estimated using the sample standard deviation. Ppk may be negative if the process mean falls outside the specification limits (because the process is producing a large proportion of defective output). Some specifications may only be one sided (for example, strength). For specifications that only have a lower limit, \hat_ = ; for those that only have an upper limit, \hat_ = . Practitioners may also encounter \hat_ = \frac , a metric that does not account for process per ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Process Capability
The process capability is a measurable property of a Process (engineering), process to the specification, expressed as a process capability index (e.g., Cpk or Cpm) or as a process performance index (e.g., Ppk or Ppm). The output of this measurement is often illustrated by a histogram and calculations that predict how many parts will be produced out of specification (OOS). Two parts of process capability are: # Measure the variability of the output of a process, and # Compare that variability with a proposed specification or product tolerance Capabilities The input of a process usually has at least one or more measurable characteristics that are used to specify outputs. These can be analyzed statistically; where the output data shows a normal distribution the process can be described by the process mean (average) and the standard deviation. A process needs to be established with appropriate process controls in place. A control chart analysis is used to determine whether the p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
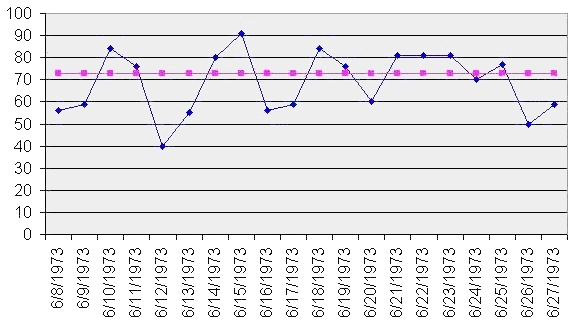
Run Chart
A run chart, also known as a run-sequence plot is a graph that displays observed data in a time sequence. Often, the data displayed represent some aspect of the output or performance of a manufacturing or other business process. It is therefore a form of line chart. Overview Run sequence plots are an easy way to graphically summarize a univariate data set. A common assumption of univariate data sets is that they behave like:NIST/SEMATECH (2003)"Run-Sequence Plot"In: ''e-Handbook of Statistical Methods'' 6/01/2003 (Date created). * random drawings; * from a fixed distribution; * with a common location; and * with a common scale. With run sequence plots, shifts in location and scale are typically quite evident. Also, outliers can easily be detected. Examples could include measurements of the fill level of bottles filled at a bottling plant or the water temperature of a dishwashing machine each time it is run. Time is generally represented on the horizontal (x) axis and the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Micrometre
The micrometre (English in the Commonwealth of Nations, Commonwealth English as used by the International Bureau of Weights and Measures; SI symbol: μm) or micrometer (American English), also commonly known by the non-SI term micron, is a unit of length in the International System of Units (SI) equalling (SI standard prefix "micro-" = ); that is, one millionth of a metre (or one thousandth of a millimetre, , or about ). The nearest smaller common SI Unit, SI unit is the nanometre, equivalent to one thousandth of a micrometre, one millionth of a millimetre or one billionth of a metre (). The micrometre is a common unit of measurement for wavelengths of infrared radiation as well as sizes of biological cell (biology), cells and bacteria, and for grading wool by the diameter of the fibres. The width of a single human hair ranges from approximately 20 to . Examples Between 1 μm and 10 μm: * 1–10 μm – length of a typical bacterium * 3–8 μm – width of str ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Control Chart
Control charts are graphical plots used in production control to determine whether quality and manufacturing processes are being controlled under stable conditions. (ISO 7870-1) The hourly status is arranged on the graph, and the occurrence of abnormalities is judged based on the presence of data that differs from the conventional trend or deviates from the control limit line. Control charts are classified into Shewhart individuals control chart (ISO 7870-2) and CUSUM(CUsUM)(or cumulative sum control chart)(ISO 7870-4). Control charts, also known as Shewhart charts (after Walter A. Shewhart) or process-behavior charts, are a statistical process control tool used to determine if a manufacturing or business process is in a state of control. It is more appropriate to say that the control charts are the graphical device for statistical process monitoring (SPM). Traditional control charts are mostly designed to monitor process parameters when the underlying form of the process ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normally Distributed
In probability theory and statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real number, real-valued random variable. The general form of its probability density function is f(x) = \frac e^\,. The parameter is the Mean#Mean of a probability distribution, mean or expected value, expectation of the distribution (and also its median and mode (statistics), mode), while the parameter \sigma^2 is the variance. The standard deviation of the distribution is (sigma). A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural science, natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Density Function
In probability theory, a probability density function (PDF), density function, or density of an absolutely continuous random variable, is a Function (mathematics), function whose value at any given sample (or point) in the sample space (the set of possible values taken by the random variable) can be interpreted as providing a ''relative likelihood'' that the value of the random variable would be equal to that sample. Probability density is the probability per unit length, in other words, while the ''absolute likelihood'' for a continuous random variable to take on any particular value is 0 (since there is an infinite set of possible values to begin with), the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would be close to one sample compared to the other sample. More precisely, the PDF is used to specify the probability of the random variable falling ''within ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parts Per Million
In science and engineering, the parts-per notation is a set of pseudo-units to describe the small values of miscellaneous dimensionless quantity, dimensionless quantities, e.g. mole fraction or mass fraction (chemistry), mass fraction. Since these fraction (mathematics), fractions are quantity-per-quantity measures, they are pure numbers with no associated units of measurement. Commonly used are * parts-per-million - ppm, * parts-per-billion - ppb, * parts-per-trillion - ppt, * parts-per-quadrillion - ppq, This notation is not part of the International System of Units - SI system and its meaning is ambiguous. Applications Parts-per notation is often used describing dilute solutions in chemistry, for instance, the relative abundance of dissolved minerals or pollutants in water. The quantity "1 ppm" can be used for a mass fraction if a water-borne pollutant is present at one-millionth of a gram per gram of sample solution. When working with aqueous solutions, it is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Defects Per Million Opportunities
In process improvement efforts, defects per million opportunities or DPMO (or nonconformities per million opportunities (NPMO)) is a measure of process performance. It is defined as \text = \frac A defect can be defined as a nonconformance of a quality characteristic (e.g. strength, width, response time) to its specification. DPMO is stated in opportunities per million units for convenience: processes that are considered highly capable (e.g., processes of Six Sigma Six Sigma (6σ) is a set of techniques and tools for process improvement. It was introduced by American engineer Bill Smith while working at Motorola in 1986. Six Sigma strategies seek to improve manufacturing quality by identifying and removin ... quality) are those that experience fewer than 3.4 defects per million opportunities (or services provided). Note that DPMO differs from reporting defective parts per million (PPM) in that it comprehends the possibility that a unit under inspection may be found to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |