|
Preconditioning
In mathematics, preconditioning is the application of a transformation, called the preconditioner, that conditions a given problem into a form that is more suitable for numerical solving methods. Preconditioning is typically related to reducing a condition number of the problem. The preconditioned problem is then usually solved by an iterative method. Preconditioning for linear systems In linear algebra and numerical analysis, a preconditioner P of a matrix A is a matrix such that P^A has a smaller condition number than A. It is also common to call T=P^ the preconditioner, rather than P, since P itself is rarely explicitly available. In modern preconditioning, the application of T=P^, i.e., multiplication of a column vector, or a block of column vectors, by T=P^, is commonly performed in a matrix-free fashion, i.e., where neither P, nor T=P^ (and often not even A) are explicitly available in a matrix form. Preconditioners are useful in iterative methods to solve a linear ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conjugate Gradient Method
In mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is positive-definite. The conjugate gradient method is often implemented as an iterative algorithm, applicable to sparse systems that are too large to be handled by a direct implementation or other direct methods such as the Cholesky decomposition. Large sparse systems often arise when numerically solving partial differential equations or optimization problems. The conjugate gradient method can also be used to solve unconstrained optimization problems such as energy minimization. It is commonly attributed to Magnus Hestenes and Eduard Stiefel, who programmed it on the Z4, and extensively researched it. The biconjugate gradient method provides a generalization to non-symmetric matrices. Various nonlinear conjugate gradient methods seek minima of nonlinear optimization problems. Description of the problem addressed by co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Preconditioned Conjugate Gradient Method
In mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is positive-definite. The conjugate gradient method is often implemented as an iterative algorithm, applicable to sparse systems that are too large to be handled by a direct implementation or other direct methods such as the Cholesky decomposition. Large sparse systems often arise when numerically solving partial differential equations or optimization problems. The conjugate gradient method can also be used to solve unconstrained optimization problems such as energy minimization. It is commonly attributed to Magnus Hestenes and Eduard Stiefel, who programmed it on the Z4, and extensively researched it. The biconjugate gradient method provides a generalization to non-symmetric matrices. Various nonlinear conjugate gradient methods seek minima of nonlinear optimization problems. Description of the problem addressed by conju ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
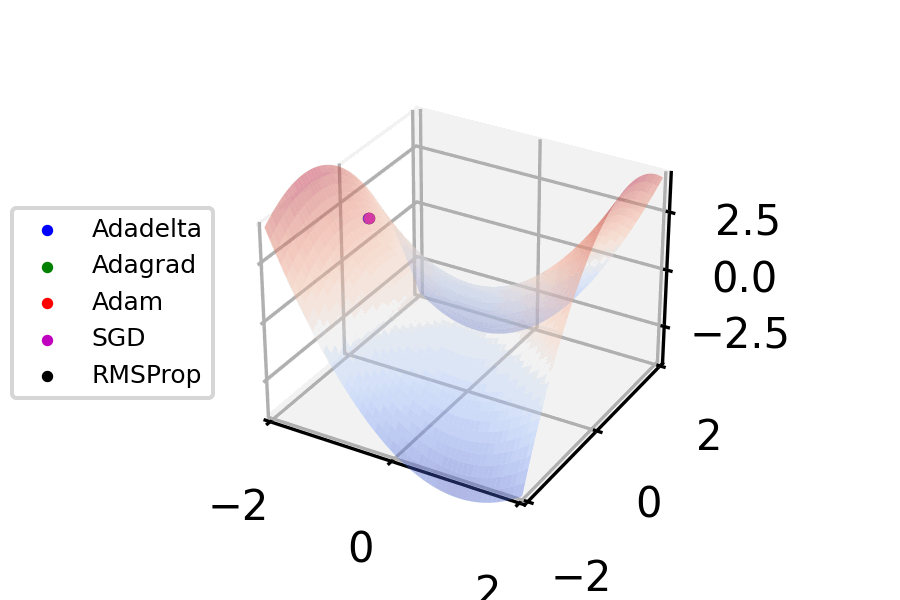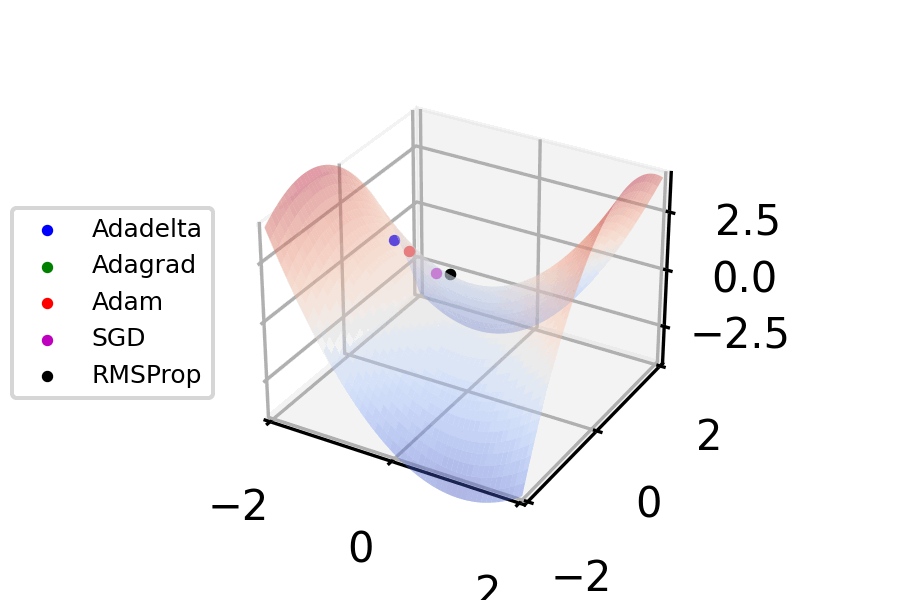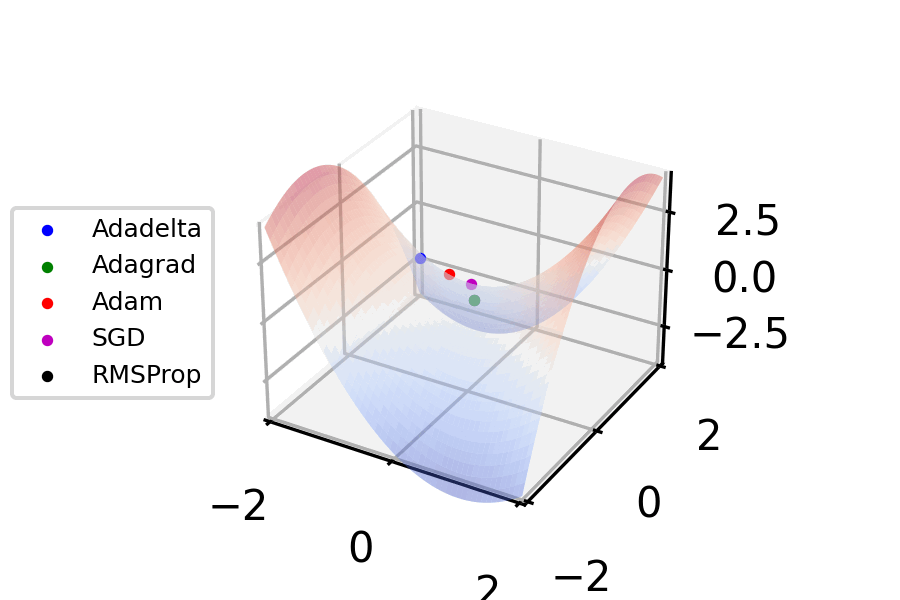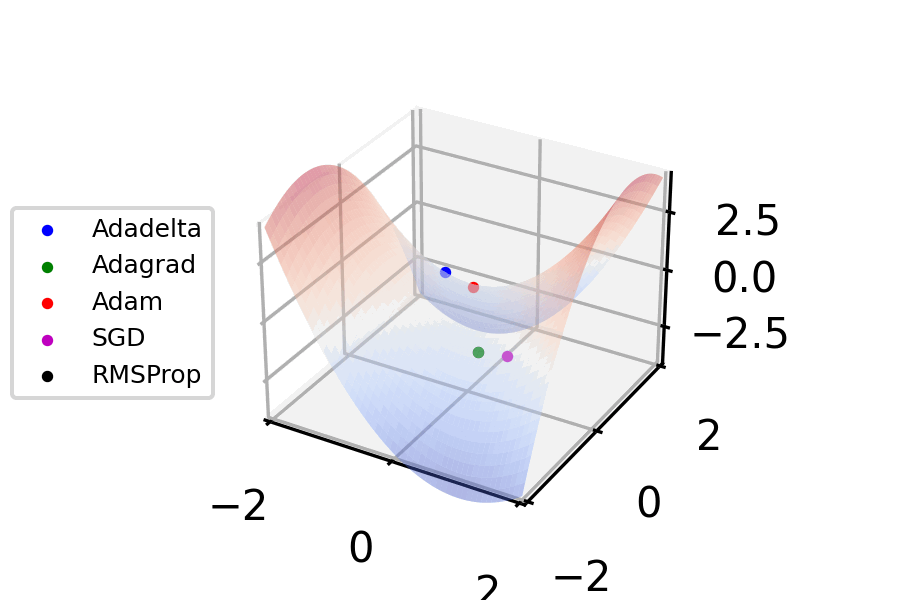
Gradient Descent
In mathematics, gradient descent (also often called steepest descent) is a first-order iterative optimization algorithm for finding a local minimum of a differentiable function. The idea is to take repeated steps in the opposite direction of the gradient (or approximate gradient) of the function at the current point, because this is the direction of steepest descent. Conversely, stepping in the direction of the gradient will lead to a local maximum of that function; the procedure is then known as gradient ascent. Gradient descent is generally attributed to Augustin-Louis Cauchy, who first suggested it in 1847. Jacques Hadamard independently proposed a similar method in 1907. Its convergence properties for non-linear optimization problems were first studied by Haskell Curry in 1944, with the method becoming increasingly well-studied and used in the following decades. Description Gradient descent is based on the observation that if the multi-variable function F(\mathbf) is def ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multigrid
In numerical analysis, a multigrid method (MG method) is an algorithm for solving differential equations using a hierarchy of discretizations. They are an example of a class of techniques called multiresolution methods, very useful in problems exhibiting multiple scales of behavior. For example, many basic relaxation methods exhibit different rates of convergence for short- and long-wavelength components, suggesting these different scales be treated differently, as in a Fourier analysis approach to multigrid. MG methods can be used as solvers as well as preconditioners. The main idea of multigrid is to accelerate the convergence of a basic iterative method (known as relaxation, which generally reduces short-wavelength error) by a ''global'' correction of the fine grid solution approximation from time to time, accomplished by solving a coarse problem. The coarse problem, while cheaper to solve, is similar to the fine grid problem in that it also has short- and long-wavelength errors ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Biconjugate Gradient Method
In mathematics, more specifically in numerical linear algebra, the biconjugate gradient method is an algorithm to solve systems of linear equations :A x= b.\, Unlike the conjugate gradient method, this algorithm does not require the matrix A to be self-adjoint, but instead one needs to perform multiplications by the conjugate transpose . The algorithm # Choose initial guess x_0\,, two other vectors x_0^* and b^*\, and a preconditioner M\, # r_0 \leftarrow b-A\, x_0\, # r_0^* \leftarrow b^*-x_0^*\, A # p_0 \leftarrow M^ r_0\, # p_0^* \leftarrow r_0^*M^\, # for k=0, 1, \ldots do ## \alpha_k \leftarrow \, ## x_ \leftarrow x_k + \alpha_k \cdot p_k\, ## x_^* \leftarrow x_k^* + \overline\cdot p_k^*\, ## r_ \leftarrow r_k - \alpha_k \cdot A p_k\, ## r_^* \leftarrow r_k^*- \overline \cdot p_k^*\, A ## \beta_k \leftarrow \, ## p_ \leftarrow M^ r_ + \beta_k \cdot p_k\, ## p_^* \leftarrow r_^*M^ + \overline\cdot p_k^*\, In the above formulation, the computed r_k\, and r_k^* satisfy :r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diagonally Dominant Matrix
In mathematics, a square matrix is said to be diagonally dominant if, for every row of the matrix, the magnitude of the diagonal entry in a row is larger than or equal to the sum of the magnitudes of all the other (non-diagonal) entries in that row. More precisely, the matrix ''A'' is diagonally dominant if :, a_, \geq \sum_ , a_, \quad\text i \, where ''a''''ij'' denotes the entry in the ''i''th row and ''j''th column. Note that this definition uses a weak inequality, and is therefore sometimes called ''weak diagonal dominance''. If a strict inequality (>) is used, this is called ''strict diagonal dominance''. The unqualified term ''diagonal dominance'' can mean both strict and weak diagonal dominance, depending on the context. Variations The definition in the first paragraph sums entries across each row. It is therefore sometimes called ''row diagonal dominance''. If one changes the definition to sum down each column, this is called ''column diagonal dominance''. Any stric ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Evgenii Georgievich D'yakonov
Evgenii Georgievich Dyakonov (russian: Евгений Георгиевич Дьяконов) (July 2, 1935 – August 11, 2006) was a Russian mathematician. Dyakonov was a Ph.D. student of Sergei Sobolev. He worked at the Moscow State University. He authored over hundred papers and several books. Dyakonov was recognized for his pioneering work in the 60s–80s on efficient spectrally equivalent preconditioning for linear systems and eigenvalue problems. In the last decade, strengthened Sobolev space In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of ''Lp''-norms of the function together with its derivatives up to a given order. The derivatives are understood in a suitable weak sense ...s became Dyakonov's main topic of research, e.g., (Dyakonov, 2004). References External links Evgenii D'yakonov — scientific works on the website Math-Net.Ru* * obituary on NA Digest by Andrew Knyazev. Russian ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Differential Equations
In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a multivariable function. The function is often thought of as an "unknown" to be solved for, similarly to how is thought of as an unknown number to be solved for in an algebraic equation like . However, it is usually impossible to write down explicit formulas for solutions of partial differential equations. There is, correspondingly, a vast amount of modern mathematical and scientific research on methods to numerically approximate solutions of certain partial differential equations using computers. Partial differential equations also occupy a large sector of pure mathematical research, in which the usual questions are, broadly speaking, on the identification of general qualitative features of solutions of various partial differential equations, such as existence, uniqueness, regularity, and stability. Among the many open questions are the e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Gradient Descent
Stochastic gradient descent (often abbreviated SGD) is an iterative method for optimizing an objective function with suitable smoothness properties (e.g. differentiable or subdifferentiable). It can be regarded as a stochastic approximation of gradient descent optimization, since it replaces the actual gradient (calculated from the entire data set) by an estimate thereof (calculated from a randomly selected subset of the data). Especially in high-dimensional optimization problems this reduces the very high computational burden, achieving faster iterations in trade for a lower convergence rate. While the basic idea behind stochastic approximation can be traced back to the Robbins–Monro algorithm of the 1950s, stochastic gradient descent has become an important optimization method in machine learning. Background Both statistical estimation and machine learning consider the problem of minimizing an objective function that has the form of a sum: : Q(w) = \frac\sum_^n Q_i(w), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadratic Form
In mathematics, a quadratic form is a polynomial with terms all of degree two ("form" is another name for a homogeneous polynomial). For example, :4x^2 + 2xy - 3y^2 is a quadratic form in the variables and . The coefficients usually belong to a fixed field , such as the real or complex numbers, and one speaks of a quadratic form over . If K=\mathbb R, and the quadratic form takes zero only when all variables are simultaneously zero, then it is a definite quadratic form, otherwise it is an isotropic quadratic form. Quadratic forms occupy a central place in various branches of mathematics, including number theory, linear algebra, group theory (orthogonal group), differential geometry (Riemannian metric, second fundamental form), differential topology ( intersection forms of four-manifolds), and Lie theory (the Killing form). Quadratic forms are not to be confused with a quadratic equation, which has only one variable and includes terms of degree two or less. A quadratic form is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scalar Product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a scalar as a result". It is also used sometimes for other symmetric bilinear forms, for example in a pseudo-Euclidean space. is an algebraic operation that takes two equal-length sequences of numbers (usually coordinate vectors), and returns a single number. In Euclidean geometry, the dot product of the Cartesian coordinates of two vectors is widely used. It is often called the inner product (or rarely projection product) of Euclidean space, even though it is not the only inner product that can be defined on Euclidean space (see Inner product space for more). Algebraically, the dot product is the sum of the products of the corresponding entries of the two sequences of numbers. Geometrically, it is the product of the Euclidean magnitudes of the two vectors and the cosine of the angle between them. These definitions are equivalent when using Cartesian coordinates. In mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positive-definite Matrix
In mathematics, a symmetric matrix M with real entries is positive-definite if the real number z^\textsfMz is positive for every nonzero real column vector z, where z^\textsf is the transpose of More generally, a Hermitian matrix (that is, a complex matrix equal to its conjugate transpose) is positive-definite if the real number z^* Mz is positive for every nonzero complex column vector z, where z^* denotes the conjugate transpose of z. Positive semi-definite matrices are defined similarly, except that the scalars z^\textsfMz and z^* Mz are required to be positive ''or zero'' (that is, nonnegative). Negative-definite and negative semi-definite matrices are defined analogously. A matrix that is not positive semi-definite and not negative semi-definite is sometimes called indefinite. A matrix is thus positive-definite if and only if it is the matrix of a positive-definite quadratic form or Hermitian form. In other words, a matrix is positive-definite if and only if it defines a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
