|
Positional Angle
In astronomy, position angle (usually abbreviated PA) is the convention for measuring angles on the sky. The International Astronomical Union defines it as the angle measured relative to the north celestial pole (NCP), turning positive into the direction of the right ascension. In the standard (non-flipped) images, this is a counterclockwise measure relative to the axis into the direction of positive declination. In the case of observed visual binary stars, it is defined as the angular offset of the secondary star from the primary relative to the north celestial pole. As the example illustrates, if one were observing a hypothetical binary star with a PA of 135°, that means an imaginary line in the eyepiece drawn from the north celestial pole to the primary (P) would be offset from the secondary (S) such that the angle would be 135°. When graphing visual binaries, the NCP is, as in the illustration, normally drawn from the center point (origin) that is the Primary downward& ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Position Angle
In astronomy, position angle (usually abbreviated PA) is the convention for measuring angles on the sky. The International Astronomical Union defines it as the angle measured relative to the north celestial pole (NCP), turning positive into the direction of the right ascension. In the standard (non-flipped) images, this is a counterclockwise measure relative to the axis into the direction of positive declination. In the case of observed visual binary stars, it is defined as the angular offset of the secondary star from the primary relative to the north celestial pole. As the example illustrates, if one were observing a hypothetical binary star with a PA of 135°, that means an imaginary line in the eyepiece drawn from the north celestial pole to the primary (P) would be offset from the secondary (S) such that the angle would be 135°. When graphing visual binaries, the NCP is, as in the illustration, normally drawn from the center point (origin) that is the Primary downward&nd ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great-circle Distance
The great-circle distance, orthodromic distance, or spherical distance is the distance along a great circle. It is the shortest distance between two points on the surface of a sphere, measured along the surface of the sphere (as opposed to a straight line through the sphere's interior). The distance between two points in Euclidean space is the length of a straight line between them, but on the sphere there are no straight lines. In spaces with curvature, straight lines are replaced by geodesics. Geodesics on the sphere are circles on the sphere whose centers coincide with the center of the sphere, and are called 'great circles'. The determination of the great-circle distance is part of the more general problem of great-circle navigation, which also computes the azimuths at the end points and intermediate way-points. Through any two points on a sphere that are not antipodal points (directly opposite each other), there is a unique great circle. The two points separate the gre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
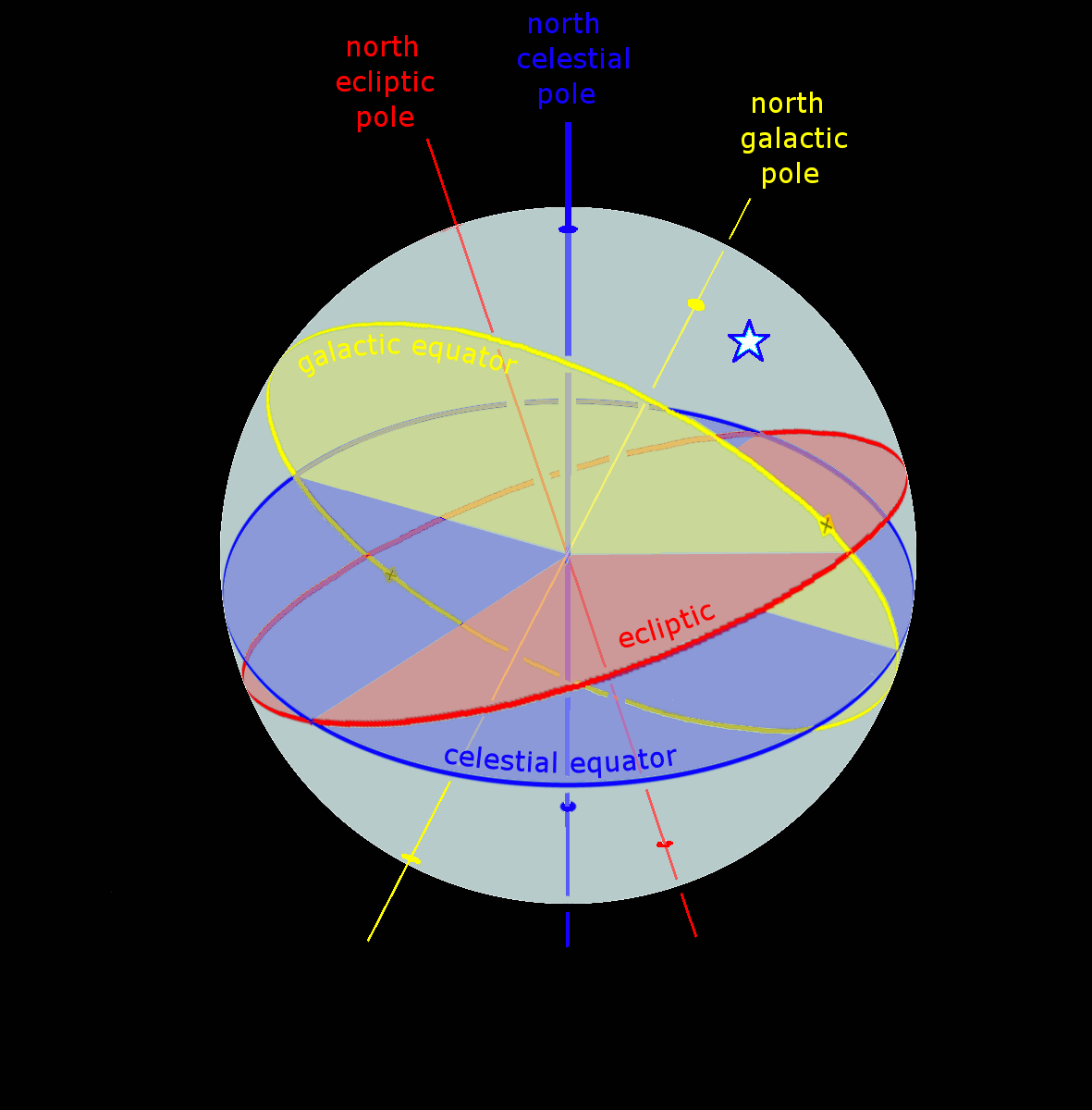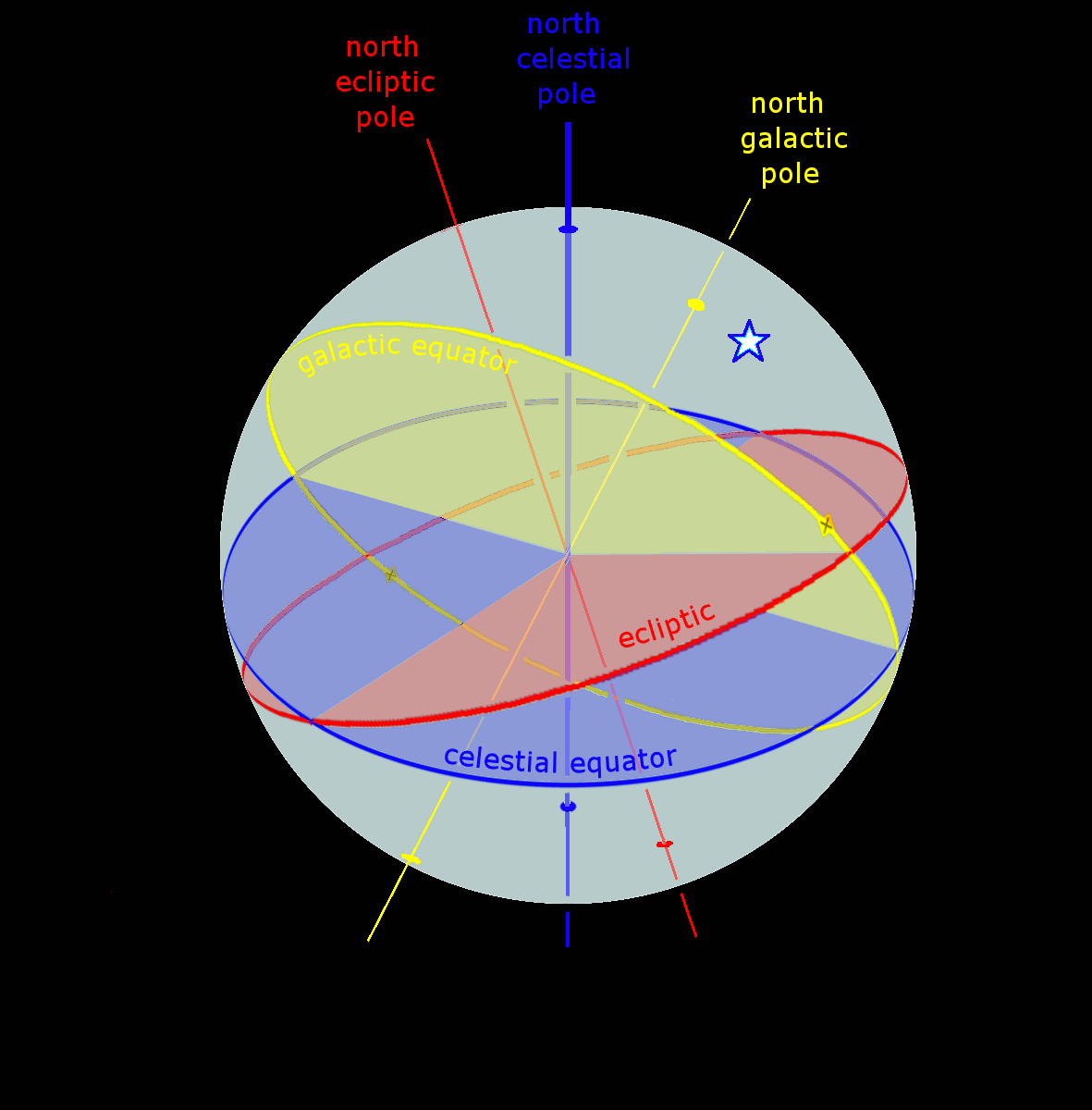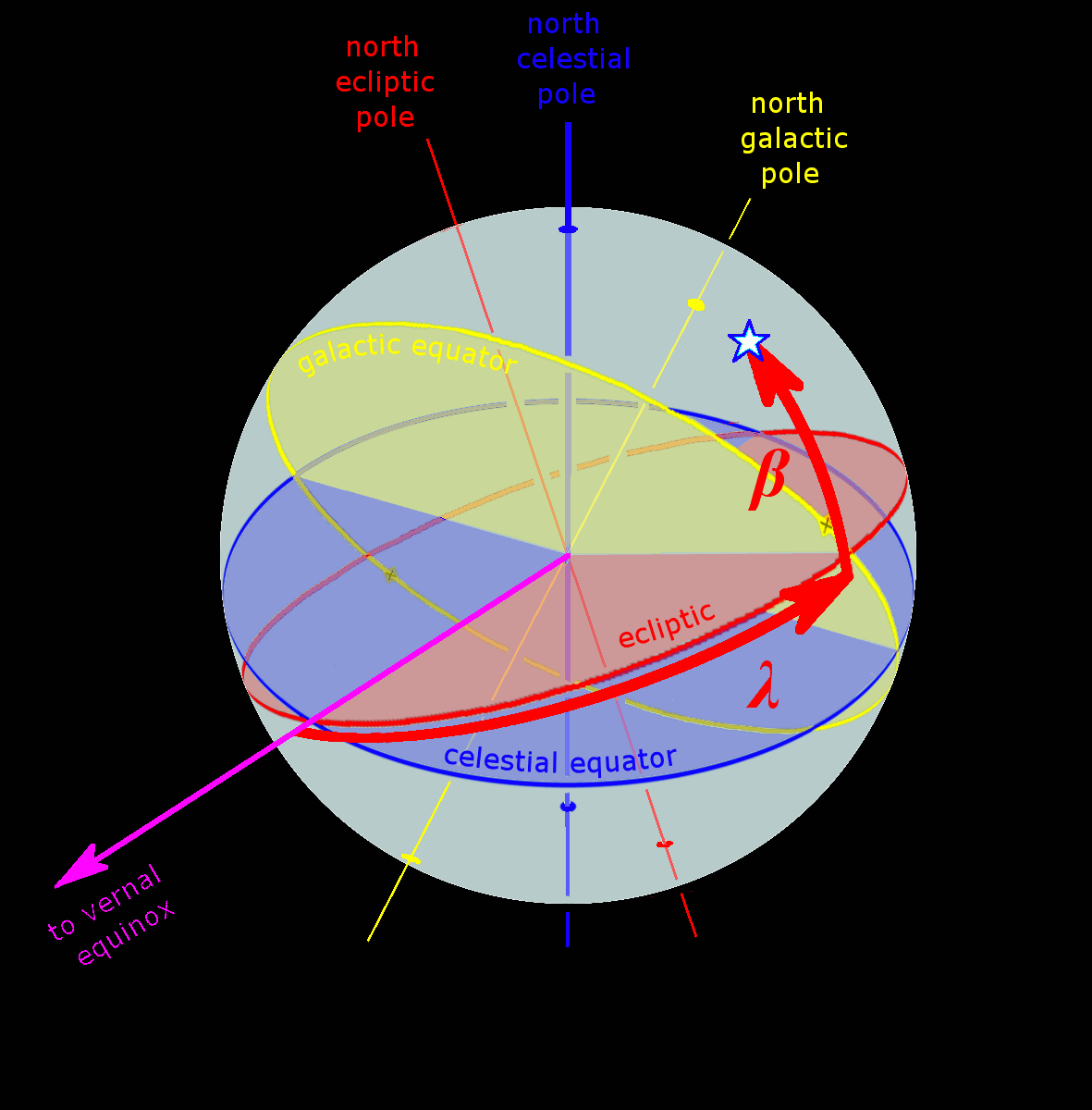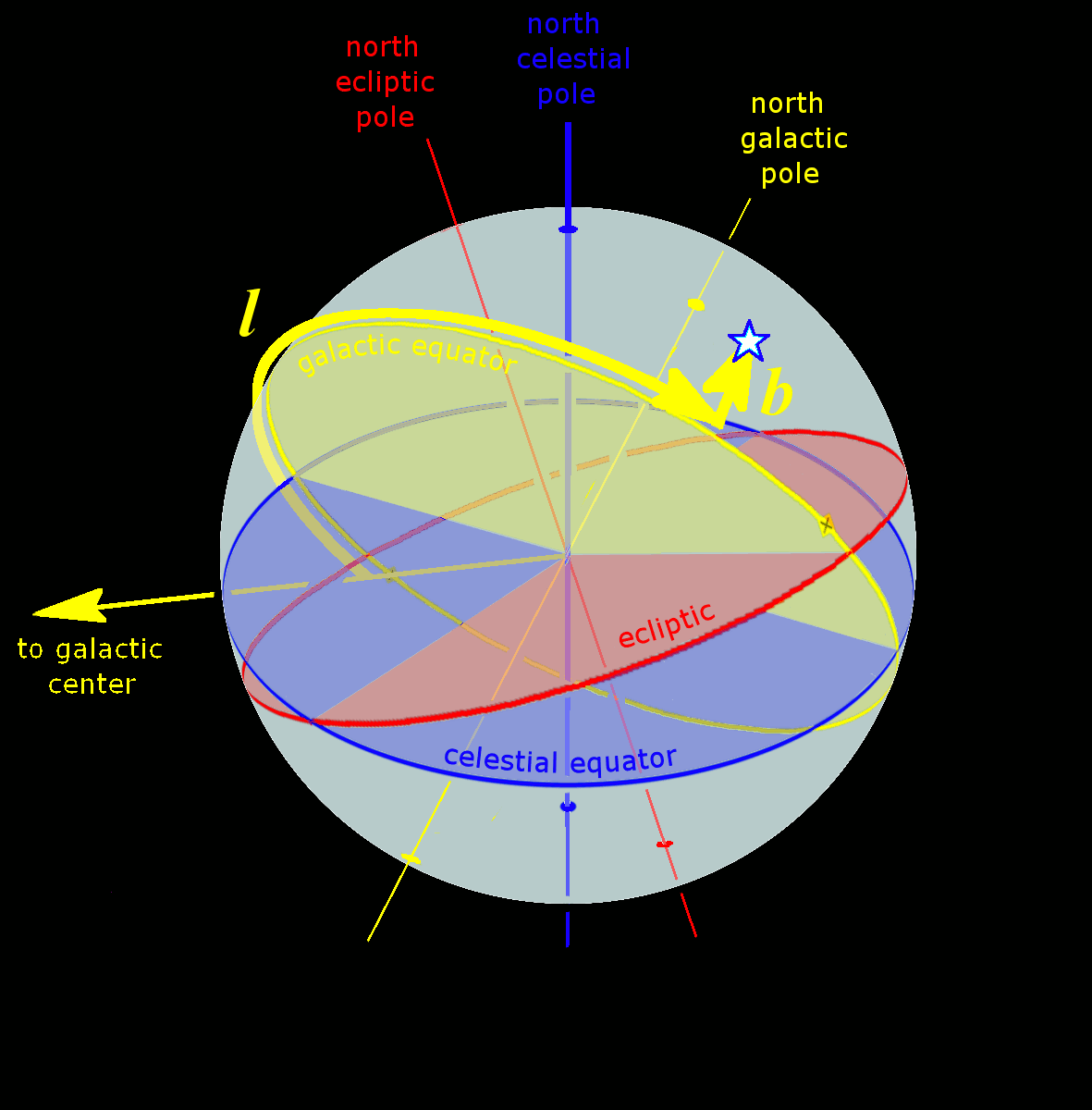
Astronomical Coordinate Systems
Astronomical coordinate systems are organized arrangements for specifying positions of satellites, planets, stars, galaxies, and other celestial objects relative to physical reference points available to a situated observer (e.g. the true horizon and north cardinal direction to an observer situated on the Earth's surface). Coordinate systems in astronomy can specify an object's position in three-dimensional space or plot merely its direction on a celestial sphere, if the object's distance is unknown or trivial. Spherical coordinates, projected on the celestial sphere, are analogous to the geographic coordinate system used on the surface of Earth. These differ in their choice of fundamental plane, which divides the celestial sphere into two equal hemispheres along a great circle. Rectangular coordinates, in appropriate units, have the same fundamental () plane and primary (-axis) direction, such as a rotation axis. Each coordinate system is named after its choice of fundamental ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cambridge University Press
Cambridge University Press is the university press of the University of Cambridge. Granted letters patent by Henry VIII of England, King Henry VIII in 1534, it is the oldest university press A university press is an academic publishing house specializing in monographs and scholarly journals. Most are nonprofit organizations and an integral component of a large research university. They publish work that has been reviewed by schola ... in the world. It is also the King's Printer. Cambridge University Press is a department of the University of Cambridge and is both an academic and educational publisher. It became part of Cambridge University Press & Assessment, following a merger with Cambridge Assessment in 2021. With a global sales presence, publishing hubs, and offices in more than 40 Country, countries, it publishes over 50,000 titles by authors from over 100 countries. Its publishing includes more than 380 academic journals, monographs, reference works, school and uni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Distance
Angular distance \theta (also known as angular separation, apparent distance, or apparent separation) is the angle between the two sightlines, or between two point objects as viewed from an observer. Angular distance appears in mathematics (in particular geometry and trigonometry) and all natural sciences (e.g. astronomy and geophysics). In the classical mechanics of rotating objects, it appears alongside angular velocity, angular acceleration, angular momentum, moment of inertia and torque. Use The term ''angular distance'' (or ''separation'') is technically synonymous with ''angle'' itself, but is meant to suggest the linear distance between objects (for instance, a couple of stars observed from Earth). Measurement Since the angular distance (or separation) is conceptually identical to an angle, it is measured in the same units, such as degrees or radians, using instruments such as goniometers or optical instruments specially designed to point in well-defined directions and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallactic Angle
In spherical astronomy, the parallactic angle is the angle between the great circle through a celestial object and the zenith, and the hour circle of the object. It is usually denoted ''q''. In the triangle zenith—object—celestial pole, the parallactic angle will be the position angle of the zenith at the celestial object. Despite its name, this angle is unrelated with parallax. The parallactic angle is zero or 180° when the object crosses the meridian. Uses For ground-based observatories, the Earth atmosphere acts like a prism which disperses light of different wavelengths such that a star generates a rainbow along the direction that points to the zenith. So given an astronomical picture with a coordinate system with a known direction to the Celestial pole, the parallactic angle represents the direction of that prismatic effect relative to that reference direction. Knowledge of that angle is needed to align Atmospheric Dispersion Correctors with the beam axis of the teles ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triple Product
In geometry and algebra, the triple product is a product of three 3-dimensional vectors, usually Euclidean vectors. The name "triple product" is used for two different products, the scalar-valued scalar triple product and, less often, the vector-valued vector triple product. Scalar triple product The scalar triple product (also called the mixed product, box product, or triple scalar product) is defined as the dot product of one of the vectors with the cross product of the other two. Geometric interpretation Geometrically, the scalar triple product : \mathbf\cdot(\mathbf\times \mathbf) is the (signed) volume of the parallelepiped defined by the three vectors given. Here, the parentheses may be omitted without causing ambiguity, since the dot product cannot be evaluated first. If it were, it would leave the cross product of a scalar and a vector, which is not defined. Properties * The scalar triple product is unchanged under a circular shift of its three operands (a, b, c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cross Product
In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space (named here E), and is denoted by the symbol \times. Given two linearly independent vectors and , the cross product, (read "a cross b"), is a vector that is perpendicular to both and , and thus normal to the plane containing them. It has many applications in mathematics, physics, engineering, and computer programming. It should not be confused with the dot product (projection product). If two vectors have the same direction or have the exact opposite direction from each other (that is, they are ''not'' linearly independent), or if either one has zero length, then their cross product is zero. More generally, the magnitude of the product equals the area of a parallelogram with the vectors for sides; in particular, the magnitude of the product of two perpendic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Trigonometry
Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the sides and angles of spherical triangles, traditionally expressed using trigonometric functions. On the sphere, geodesics are great circles. Spherical trigonometry is of great importance for calculations in astronomy, geodesy, and navigation. The origins of spherical trigonometry in Greek mathematics and the major developments in Islamic mathematics are discussed fully in History of trigonometry and Mathematics in medieval Islam. The subject came to fruition in Early Modern times with important developments by John Napier, Delambre and others, and attained an essentially complete form by the end of the nineteenth century with the publication of Todhunter's textbook ''Spherical trigonometry for the use of colleges and Schools''. Since then, significant developments have been the application of vector methods, quaternion methods, and the use of numerical methods. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dot Product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a scalar as a result". It is also used sometimes for other symmetric bilinear forms, for example in a pseudo-Euclidean space. is an algebraic operation that takes two equal-length sequences of numbers (usually coordinate vectors), and returns a single number. In Euclidean geometry, the dot product of the Cartesian coordinates of two vectors is widely used. It is often called the inner product (or rarely projection product) of Euclidean space, even though it is not the only inner product that can be defined on Euclidean space (see Inner product space for more). Algebraically, the dot product is the sum of the products of the corresponding entries of the two sequences of numbers. Geometrically, it is the product of the Euclidean magnitudes of the two vectors and the cosine of the angle between them. These definitions are equivalent when using Cartesian coordinates. In mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |