|
Parallactic Angle
In spherical astronomy, the parallactic angle is the angle between the great circle through a celestial object and the zenith, and the hour circle of the object. It is usually denoted ''q''. In the triangle zenith—object—celestial pole, the parallactic angle will be the position angle of the zenith at the celestial object. Despite its name, this angle is unrelated with parallax. The parallactic angle is 0° or 180° when the object crosses the meridian. Uses For ground-based observatories, the Earth atmosphere acts like a prism which disperses light of different wavelengths such that a star generates a rainbow along the direction that points to the zenith. So given an astronomical picture with a coordinate system with a known direction to the Celestial pole, the parallactic angle represents the direction of that prismatic effect relative to that reference direction. Knowledge of that angle is needed to align Atmospheric Dispersion Correctors with the beam axis of the t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Astronomy
Spherical astronomy, or positional astronomy, is a branch of observational astronomy used to locate astronomical objects on the celestial sphere, as seen at a particular date, time, and location on Earth. It relies on the mathematical methods of spherical trigonometry and the measurements of astrometry. This is the oldest branch of astronomy and dates back to antiquity. Observations of celestial objects have been, and continue to be, important for religious and astrological purposes, as well as for timekeeping and navigation. The science of actually measuring positions of celestial objects in the sky is known as astrometry. The primary elements of spherical astronomy are celestial coordinate systems and time. The coordinates of objects on the sky are listed using the equatorial coordinate system, which is based on the projection of Earth's equator onto the celestial sphere. The position of an object in this system is given in terms of right ascension (α) and declination (δ). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Libration
In lunar astronomy, libration is the cyclic variation in the apparent position of the Moon that is perceived by observers on the Earth and caused by changes between the orbital and rotational planes of the moon. It causes an observer to see slightly different hemispheres of the surface at different times. It is similar in both cause and effect to the changes in the Moon's apparent size because of changes in lunar distance (astronomy), distance. It is caused by three mechanisms detailed below, two of which cause a relatively tiny physical libration via tidal forces exerted by the Earth. Such true librations are known as well for other moons with locked rotation. The quite different phenomenon of a trojan asteroid's movement has been called ''Trojan libration'', and ''Trojan libration point'' means Lagrangian point. Lunar libration The Moon keeps one wikt:hemisphere, hemisphere of itself facing the Earth because of tidal locking. Therefore, the first view of the far side of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equator
The equator is the circle of latitude that divides Earth into the Northern Hemisphere, Northern and Southern Hemisphere, Southern Hemispheres of Earth, hemispheres. It is an imaginary line located at 0 degrees latitude, about in circumference, halfway between the North Pole, North and South Pole, South poles. The term can also be used for any other celestial body that is roughly spherical. In three-dimensional space, spatial (3D) geometry, as applied in astronomy, the equator of a rotating spheroid (such as a planet) is the parallel (circle of latitude) at which latitude is defined to be 0°. It is an imaginary line on the spheroid, equidistant from its geographical pole, poles, dividing it into northern and southern hemispheres. In other words, it is the intersection of the spheroid with the plane (geometry), plane perpendicular to its axis of rotation and midway between its geographical poles. On and near the equator (on Earth), noontime sunlight appears almost directly o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
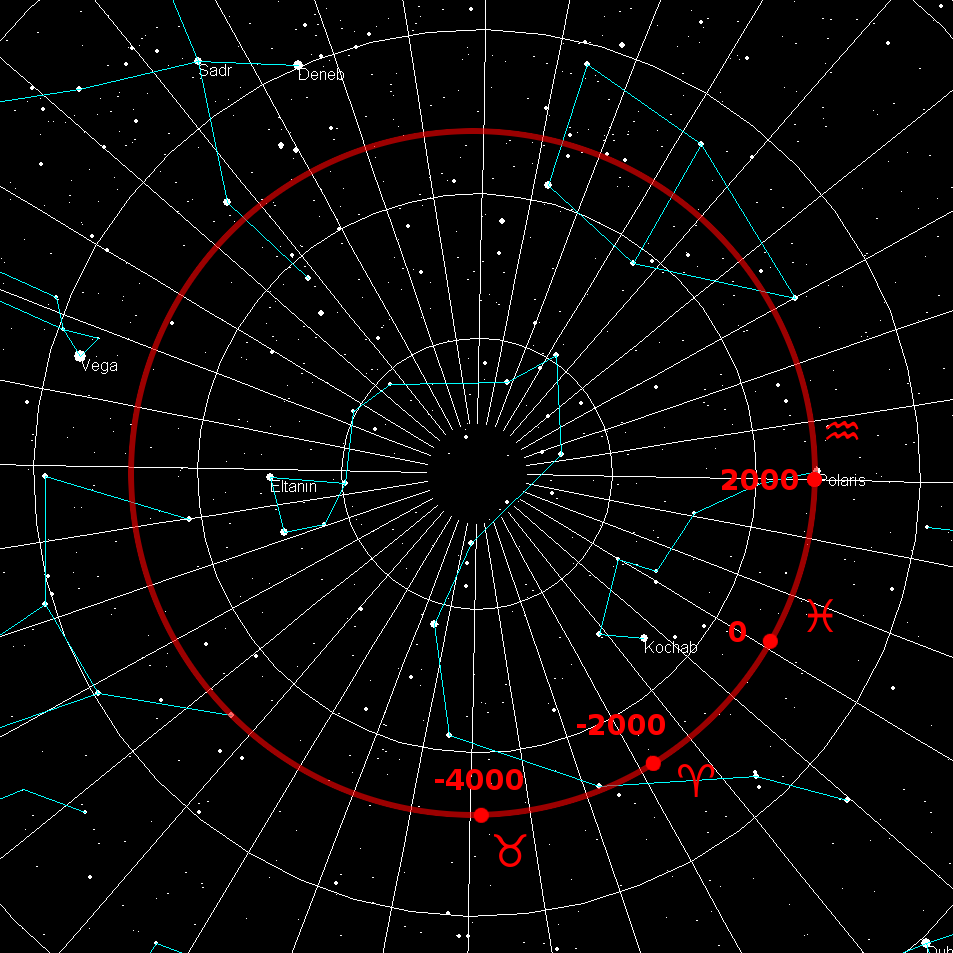
Celestial Pole
The north and south celestial poles are the two points in the sky where Earth's axis of rotation, indefinitely extended, intersects the celestial sphere. The north and south celestial poles appear permanently directly overhead to observers at Earth's North Pole and South Pole, respectively. As Earth spins on its axis, the two celestial poles remain fixed in the sky, and all other celestial points appear to rotate around them, completing one circuit per day (strictly, per sidereal day). The celestial poles are also the poles of the celestial equatorial coordinate system, meaning they have declinations of +90 degrees and −90 degrees (for the north and south celestial poles, respectively). Despite their apparently fixed positions, the celestial poles in the long term do not actually remain permanently fixed against the background of the stars. Because of a phenomenon known as the precession of the equinoxes, the poles trace out circles on the celestial sphere, with a period ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sidereal Time
Sidereal time ("sidereal" pronounced ) is a system of timekeeping used especially by astronomers. Using sidereal time and the celestial coordinate system, it is easy to locate the positions of celestial objects in the night sky. Sidereal time is a "time scale that is based on Earth's rate of rotation measured relative to the fixed stars". A sidereal day (also known as the sidereal rotation period) represents the time for one rotation about the planet axis relative to the stars. Viewed from the same location, a star seen at one position in the sky will be seen at the same position on another night at the same time of day (or night), if the day is defined as a sidereal day. This is similar to how the time kept by a sundial (Solar time) can be used to find the location of the Sun. Just as the Sun and Moon appear to rise in the east and set in the west due to the rotation of Earth, so do the stars. Both solar time and sidereal time make use of the regularity of Earth's rot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Atan2
In computing and mathematics, the function (mathematics), function atan2 is the 2-Argument of a function, argument arctangent. By definition, \theta = \operatorname(y, x) is the angle measure (in radians, with -\pi 0, \\[5mu] \arctan\left(\frac y x\right) + \pi &\text x < 0 \text y \ge 0, \\[5mu] \arctan\left(\frac y x\right) - \pi &\text x < 0 \text y < 0, \\[5mu] +\frac &\text x = 0 \text y > 0, \\[5mu] -\frac &\text x = 0 \text y < 0, \\[5mu] \text &\text x = 0 \text y = 0. \end Instead of the tangent, it can be convenient to use the half-tangent as a representation of an angle, partly because the angle has a unique half-tangent, (See tangent half-angle formula.) The expression with in the denominator should be used when and to avoid possible loss of significance in computing . When an function is unavailable, it can be computed as twice the arctangent of the half-tangent . That is, |
Spherical Trigonometry
Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the edge (geometry), sides and angles of spherical triangles, traditionally expressed using trigonometric functions. On the sphere, geodesics are great circles. Spherical trigonometry is of great importance for calculations in astronomy, geodesy, and navigation. The origins of spherical trigonometry in Greek mathematics and the major developments in Islamic mathematics are discussed fully in History of trigonometry and Mathematics in medieval Islam. The subject came to fruition in Early Modern times with important developments by John Napier, Jean Baptiste Joseph Delambre, Delambre and others, and attained an essentially complete form by the end of the nineteenth century with the publication of Todhunter's textbook ''Spherical trigonometry for the use of colleges and Schools''. Since then, significant developments have been the application of vector methods, quaternion m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
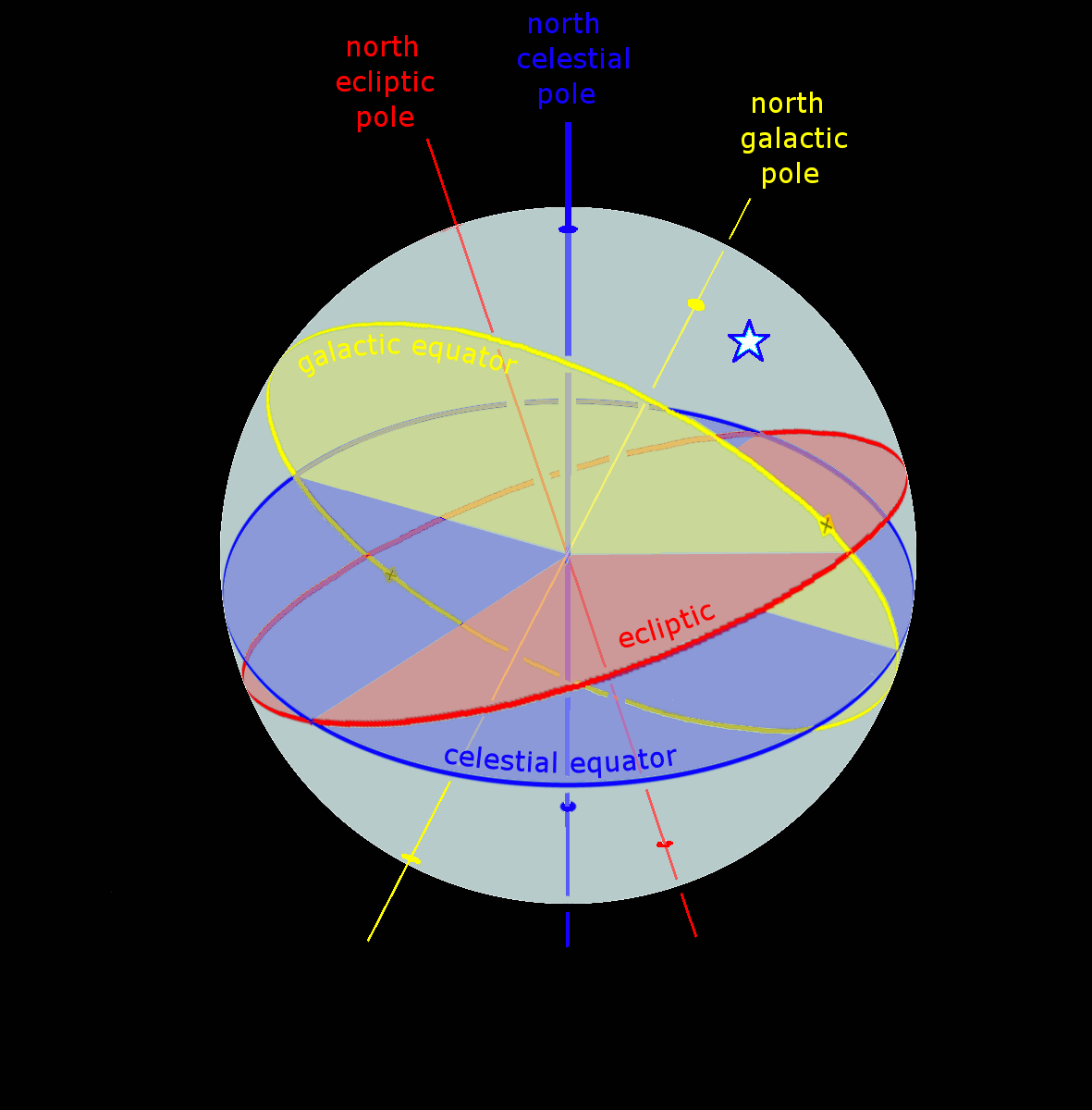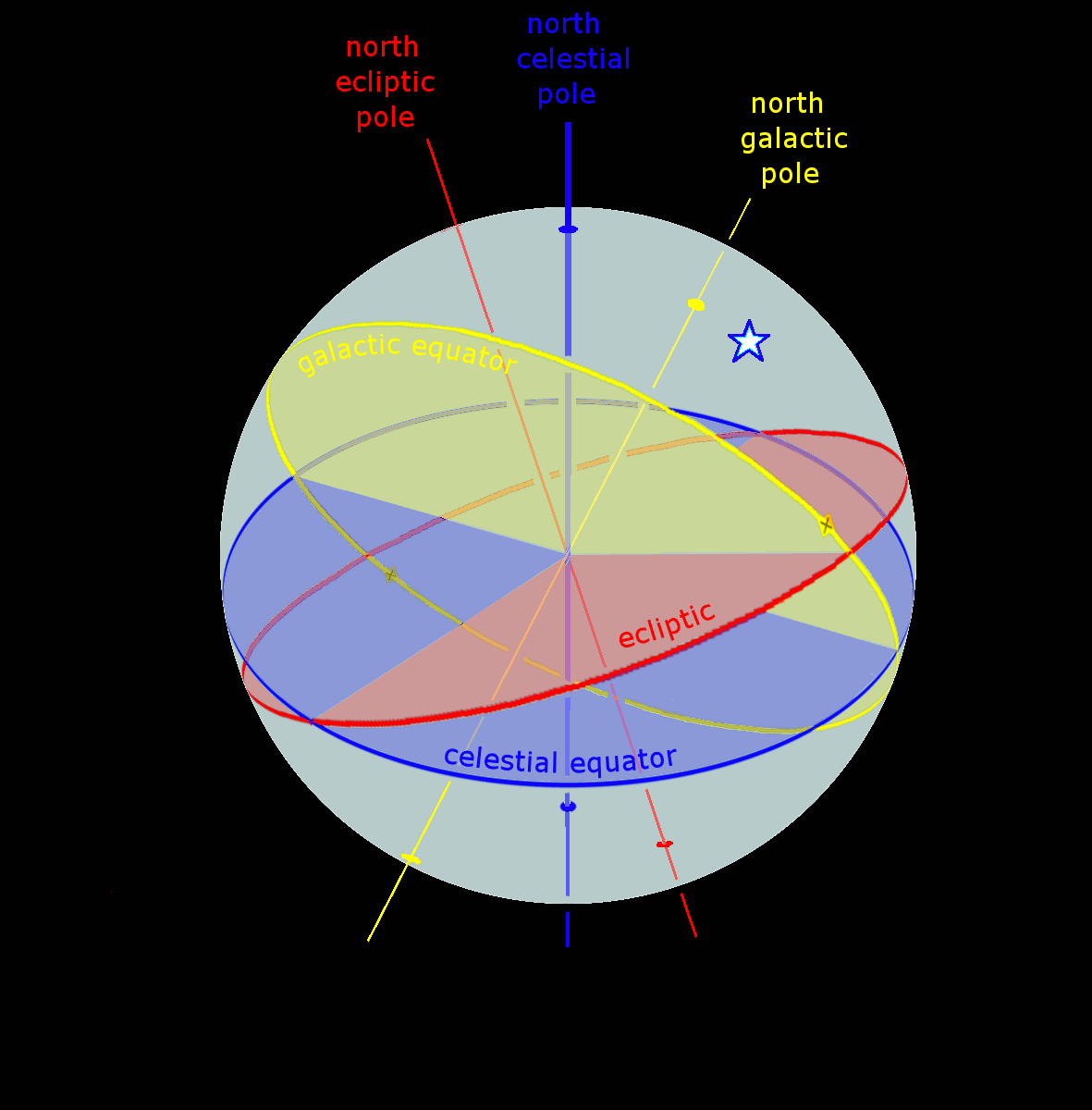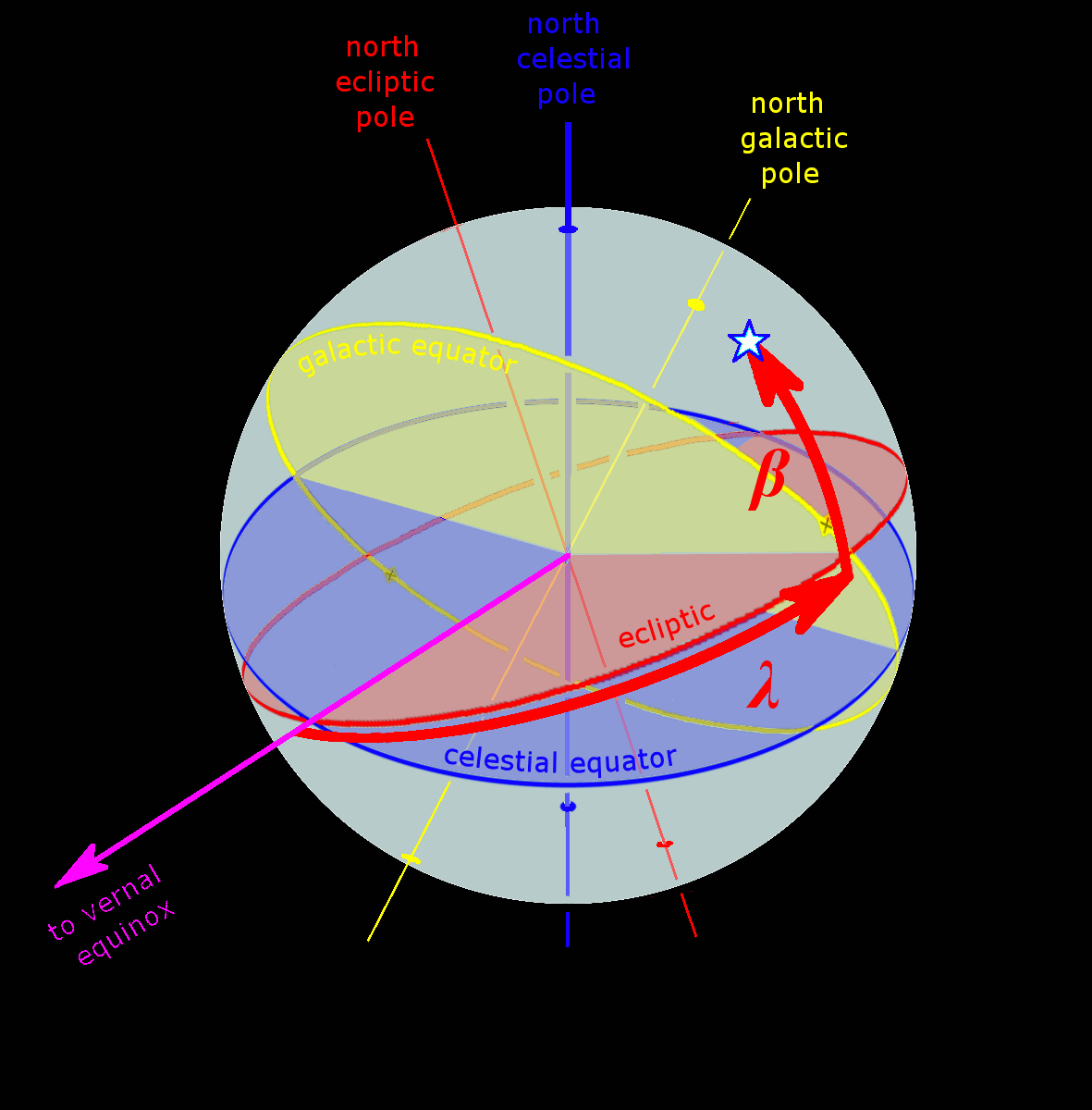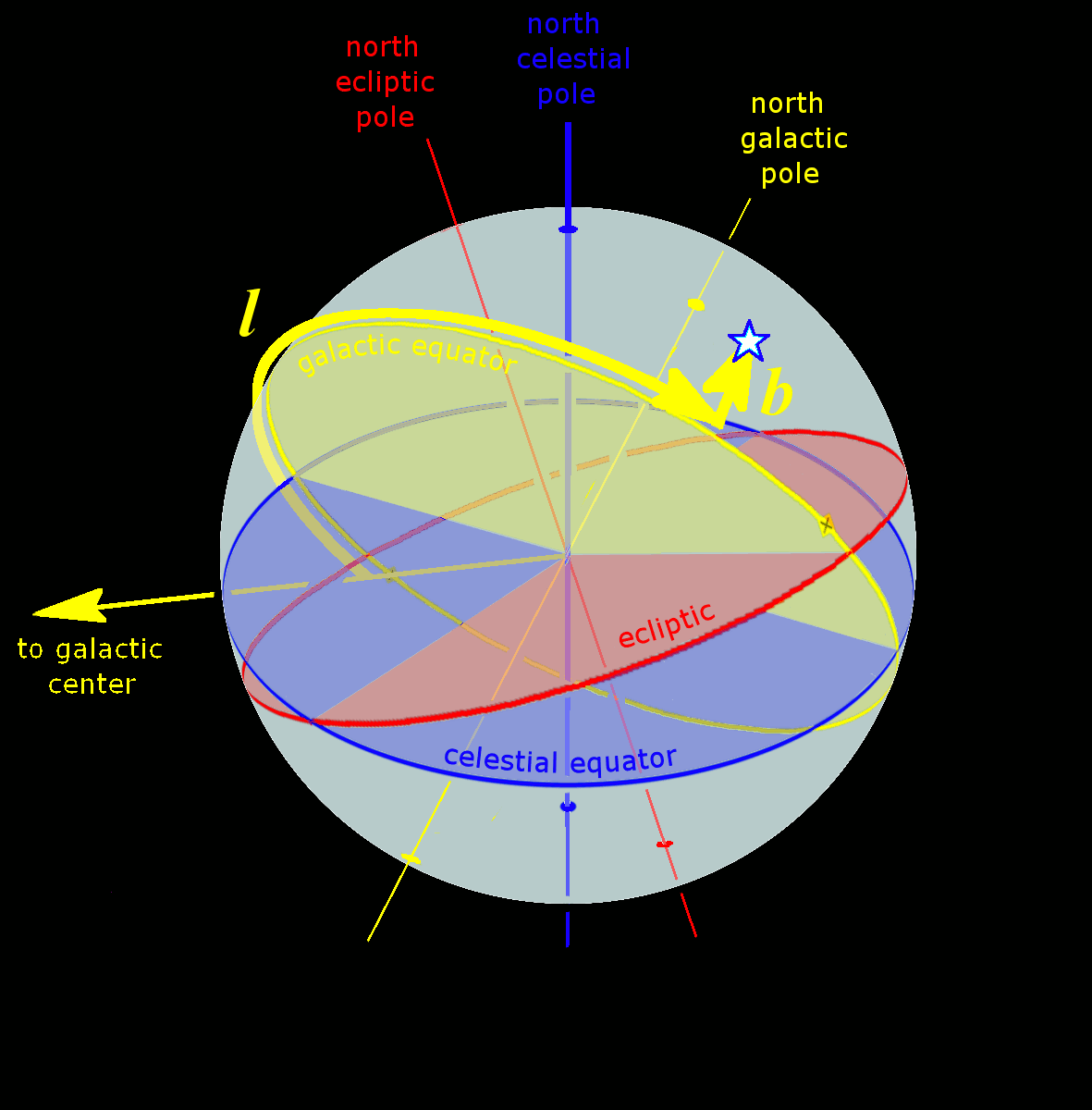
Celestial Coordinate System
In astronomy, coordinate systems are used for specifying positions of celestial objects (satellites, planets, stars, galaxies, etc.) relative to a given reference frame, based on physical reference points available to a situated observer (e.g. the true horizon and north to an observer on Earth's surface). Coordinate systems in astronomy can specify an object's relative position in three-dimensional space or plot merely by its direction on a celestial sphere, if the object's distance is unknown or trivial. Spherical coordinates, projected on the celestial sphere, are analogous to the geographic coordinate system used on the surface of Earth. These differ in their choice of fundamental plane, which divides the celestial sphere into two equal hemispheres along a great circle. Rectangular coordinates, in appropriate units, have the same fundamental () plane and primary (-axis) direction, such as an axis of rotation. Each coordinate system is named after its choice of fund ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clockwise
Two-dimensional rotation can occur in two possible directions or senses of rotation. Clockwise motion (abbreviated CW) proceeds in the same direction as a clock's hands relative to the observer: from the top to the right, then down and then to the left, and back up to the top. The opposite sense of rotation or revolution is (in Commonwealth English) anticlockwise (ACW) or (in North American English) counterclockwise (CCW). Three-dimensional rotation can have similarly defined senses when considering the corresponding angular velocity vector. Terminology Before clocks were commonplace, the terms " sunwise" and "deasil", "deiseil" and even "deocil" from the Scottish Gaelic language and from the same root as the Latin "dexter" ("right") were used for clockwise. " Widdershins" or "withershins" (from Middle Low German "weddersinnes", "opposite course") was used for counterclockwise. The terms clockwise and counterclockwise can only be applied to a rotational motion once a side ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Position Angle
In astronomy, position angle (usually abbreviated PA) is the convention for measuring angles on the sky. The International Astronomical Union defines it as the angle measured relative to the Celestial pole, north celestial pole (NCP), turning positive into the direction of the right ascension. In the standard (non-flipped) images, this is a counterclockwise measure relative to the axis into the direction of positive declination. In the case of observed Visual binary, visual binary stars, it is defined as the angular offset of the secondary star from the primary relative to the Celestial pole, north celestial pole. As the example illustrates, if one were observing a hypothetical binary star with a PA of 30°, that means an imaginary line in the eyepiece drawn from the north celestial pole to the primary (P) would be offset from the secondary (S) such that the angle would be 30°. When graphing visual binaries, the NCP is, as in the illustration, normally drawn from the center po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subsolar Point
The subsolar point on a planet or a moon is the point at which its Sun is perceived to be directly overhead (at the zenith); that is, where the Sun's rays strike the planet exactly perpendicular to its surface. The subsolar point occurs at the location on a planet or a moon where the Sun culminates at the location's zenith. This occurs at solar noon. At this point, the Sun's rays will fall exactly vertical relative to an object on the ground and thus cast no observable shadow. To an observer on a planet with an orientation and rotation similar to those of Earth, the subsolar point will appear to move westward with a speed of 1600 km/h, completing one circuit around the globe each day, approximately moving along the equator. However, it will also move north and south between the tropics over the course of a year, so will appear to spiral like a helix. The term subsolar point can also mean the point closest to the Sun on an astronomical object, even though the Sun might no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |