|
Polyhedral Map Projection
A polyhedral map projection is a map projection based on a spherical polyhedron. Typically, the polyhedron is overlaid on the globe, and each face of the polyhedron is transformed to a polygon or other shape in the plane. The best-known polyhedral map projection is Buckminster Fuller's Dymaxion map. When the spherical polyhedron faces are transformed to the faces of an ordinary polyhedron instead of laid flat in a plane, the result is a polyhedral globe. Often the polyhedron used is a Platonic solid or Archimedean solid. However, other polyhedra can be used: the AuthaGraph projection makes use of a polyhedron with 96 faces, and the myriahedral projection allows for an arbitrary large number of faces. Although interruptions between faces are common, and more common with an increasing number of faces, some maps avoid them: the Lee conformal projection only has interruptions at its border, and the AuthaGraph projection scales its faces so that the map fills a rectangle without int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dymaxion Projection
The Dymaxion map projection, also called the Fuller projection, is a kind of polyhedral map projection of the Earth's surface onto the unfolded net of an icosahedron. The resulting map is heavily interrupted in order to reduce shape and size distortion compared to other world maps, but the interruptions are chosen to lie in the ocean. The projection was invented by Buckminster Fuller. In 1943, Fuller proposed a projection onto a cuboctahedron, which he called the ''Dymaxion World'', using the name ''Dymaxion'' which he also applied to several of his other inventions. In 1954, Fuller and cartographer Shoji Sadao produced an updated Dymaxion map, the Airocean World Map, based on an icosahedron with a few of the triangular faces cut to avoid breaks in landmasses. The Dymaxion projection is intended for representations of the entire Earth. History The March 1, 1943, edition of ''Life'' magazine included a photographic essay titled "Life Presents R. Buckminster Fuller's Dymaxion ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leonardo Da Vinci
Leonardo di ser Piero da Vinci (15 April 1452 - 2 May 1519) was an Italian polymath of the High Renaissance who was active as a painter, draughtsman, engineer, scientist, theorist, sculptor, and architect. While his fame initially rested on his achievements as a painter, he has also become known for #Journals and notes, his notebooks, in which he made drawings and notes on a variety of subjects, including anatomy, astronomy, botany, cartography, painting, and palaeontology. Leonardo is widely regarded to have been a genius who epitomised the Renaissance humanism, Renaissance humanist ideal, and his List of works by Leonardo da Vinci, collective works comprise a contribution to later generations of artists matched only by that of his younger contemporary Michelangelo. Born out of wedlock to a successful notary and a lower-class woman in, or near, Vinci, Tuscany, Vinci, he was educated in Florence by the Italian painter and sculptor Andrea del Verrocchio. He began his career ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bernard J
Bernard ('' Bernhard'') is a French and West Germanic masculine given name. It has West Germanic origin and is also a surname. The name is attested from at least the 9th century. West Germanic ''Bernhard'' is composed from the two elements ''bern'' "bear" and ''hard'' "brave, hardy". Its native Old English cognate was ''Beornheard'', which was replaced or merged with the French form ''Bernard'' that was brought to England after the Norman Conquest. The name ''Bernhard'' was notably popular among Old Frisian speakers. Its wider use was popularized due to Saint Bernhard of Clairvaux (canonized in 1174). In Ireland, the name was an anglicized form of Brian. Geographical distribution Bernard is the second most common surname in France. As of 2014, 42.2% of all known bearers of the surname ''Bernard'' were residents of France (frequency 1:392), 12.5% of the United States (1:7,203), 7.0% of Haiti (1:382), 6.6% of Tanzania (1:1,961), 4.8% of Canada (1:1,896), 3.6% of Nigeria (1:12, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
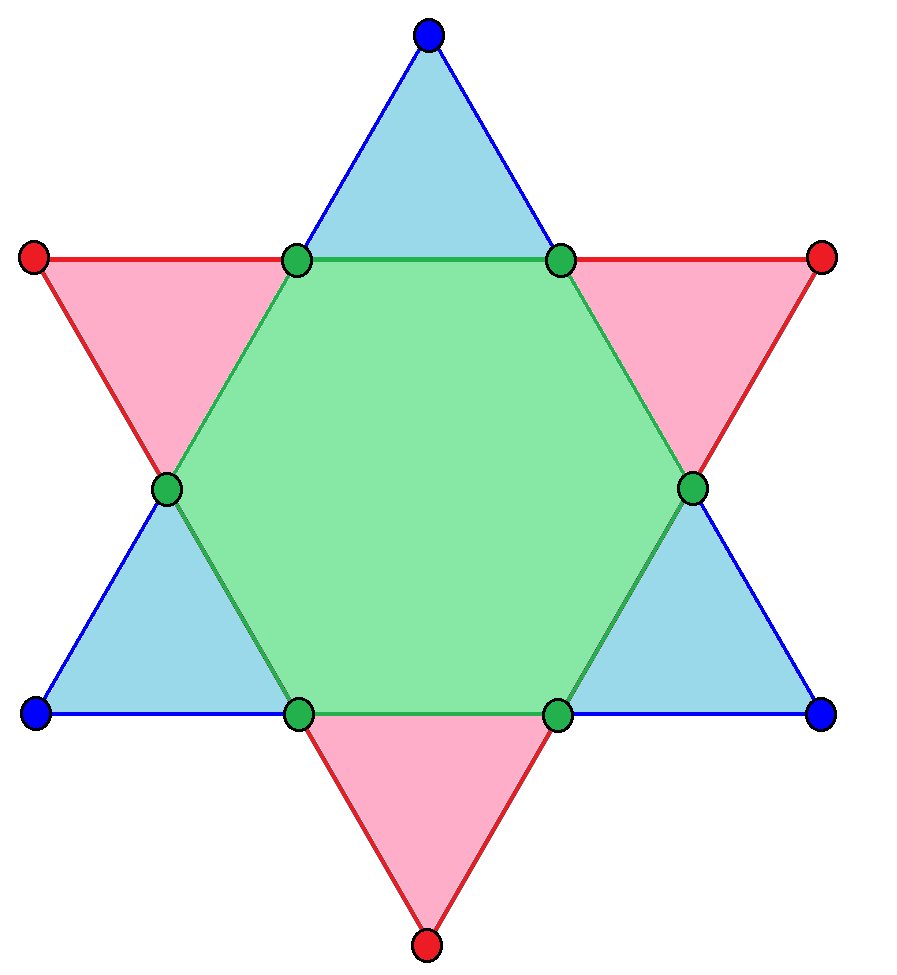
Hexagram
, can be seen as a compound polygon, compound composed of an upwards (blue here) and downwards (pink) facing equilateral triangle, with their intersection as a regular hexagon (in green). A hexagram (Greek language, Greek) or sexagram (Latin language, Latin) is a six-pointed geometric star figure with the Schläfli symbol , 2, or . The term is used to refer to a compound figure of two equilateral triangles. The intersection is a regular hexagon. The hexagram is part of an infinite series of shapes which are compounds of two n-dimensional simplex, simplices. In three dimensions, Compound of two tetrahedra, the analogous compound is the stellated octahedron, and in four dimensions the compound of two 5-cells is obtained. It has been historically used in various religious and cultural contexts and as decorative motifs. The symbol was used as a decorative motif in medieval Christian churches and Jewish synagogues. In the medieval period, a Muslim mystical symbol known as the Seal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hexagon
In geometry, a hexagon (from Greek , , meaning "six", and , , meaning "corner, angle") is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°. Regular hexagon A regular hexagon is defined as a hexagon that is both equilateral and equiangular. In other words, a hexagon is said to be regular if the edges are all equal in length, and each of its internal angle is equal to 120°. The Schläfli symbol denotes this polygon as \ . However, the regular hexagon can also be considered as the cutting off the vertices of an equilateral triangle, which can also be denoted as \mathrm\ . A regular hexagon is bicentric, meaning that it is both cyclic (has a circumscribed circle) and tangential (has an inscribed circle). The common length of the sides equals the radius of the circumscribed circle or circumcircle, which equals \tfrac times the apothem (radius of the inscribed circle). Measurement The longest diagonals of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rhombus
In plane Euclidean geometry, a rhombus (: rhombi or rhombuses) is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. The rhombus is often called a "diamond", after the Diamonds (suit), diamonds suit in playing cards which resembles the projection of an Octahedron#Orthogonal projections, octahedral diamond, or a lozenge (shape), lozenge, though the former sometimes refers specifically to a rhombus with a 60° angle (which some authors call a calisson after calisson, the French sweet—also see Polyiamond), and the latter sometimes refers specifically to a rhombus with a 45° angle. Every rhombus is simple polygon, simple (non-self-intersecting), and is a special case of a parallelogram and a Kite (geometry), kite. A rhombus with right angles is a square. Etymology The word "rhombus" comes from , meaning something that spins, which derives from the verb , roman ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oscar S
Oscar, OSCAR, or The Oscar may refer to: People and fictional and mythical characters * Oscar (given name), including lists of people and fictional characters named Oscar, Óscar or Oskar * Oscar (footballer, born 1954), Brazilian footballer José Oscar Bernardi * Oscar (footballer, born 1991), Brazilian footballer Oscar dos Santos Emboaba Júnior * Oscar (Irish mythology), son of Oisín and grandson of Finn mac Cumhall Places in the United States * Oscar, Kentucky, an unincorporated community * Oscar, Louisiana, an unincorporated community * Oscar, Missouri, an unincorporated community * Oscar, Oklahoma, an unincorporated community * Oscar, Pennsylvania, an unincorporated community * Oscar, Texas, an unincorporated community * Oscar, West Virginia, an unincorporated community * Oscar Township, Otter Tail County, Minnesota, a civil township * Lake Oscar (other) Animals * Oscar (bionic cat), a cat that had implants after losing both hind paws * Oscar (bull) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polyhedra
In geometry, a polyhedron (: polyhedra or polyhedrons; ) is a three-dimensional figure with flat polygonal faces, straight edges and sharp corners or vertices. The term "polyhedron" may refer either to a solid figure or to its boundary surface. The terms solid polyhedron and polyhedral surface are commonly used to distinguish the two concepts. Also, the term ''polyhedron'' is often used to refer implicitly to the whole structure formed by a solid polyhedron, its polyhedral surface, its faces, its edges, and its vertices. There are many definitions of polyhedron. Nevertheless, the polyhedron is typically understood as a generalization of a two-dimensional polygon and a three-dimensional specialization of a polytope, a more general concept in any number of dimensions. Polyhedra have several general characteristics that include the number of faces, topological classification by Euler characteristic, duality, vertex figures, surface area, volume, interior lines, Dehn invari ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adams Hemisphere-in-a-square Projection
The Adams hemisphere-in-a-square is a conformal map projection for a hemisphere. It is a transverse version of the Peirce quincuncial projection, and is named after American cartographer Oscar S. Adams, who published it in 1925.. When it is used to represent the entire sphere it is known as the Adams doubly periodic projection. Like many conformal projections, conformality fails at certain points, in this case at the four corners. See also * List of map projections * Guyou hemisphere-in-a-square projection * Doubly periodic function In mathematics, a doubly periodic function is a function defined on the complex plane and having two "periods", which are complex numbers ''u'' and ''v'' that are linearly independent as vectors over the field of real numbers. That ''u'' and ''v'' ... References Conformal projections {{geometry-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Guyou Hemisphere-in-a-square Projection
The Guyou hemisphere-in-a-square projection is a conformal map projection for the hemisphere. It is an oblique aspect of the Peirce quincuncial projection. History The projection was developed by of France in 1887. Formal description The projection can be computed as an oblique aspect of the Peirce quincuncial projection by rotating the axis 45 degrees. It can also be computed by rotating the coordinates −45 degrees before computing the stereographic projection; this projection is then remapped into a square whose coordinates are then rotated 45 degrees. Supplement No. 1 t''The Canadian Cartographer'' 13 The projection is conformal except for the four corners of each hemisphere's square. Like other conformal polygonal projections, the Guyou is a Schwarz–Christoffel mapping. Properties Its properties are very similar to those of the Peirce quincuncial projection: * Each hemisphere is represented as a square, the sphere as a rectangle of aspect ratio 2:1. * The part ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Peirce Quincuncial Projection
The Peirce quincuncial projection is the conformal map projection from the sphere to an unfolded square dihedron, developed by Charles Sanders Peirce in 1879. Each octant (solid geometry), octant projects onto an Special right triangle#45-45-90 triangle, isosceles right triangle, and these are arranged into a square. The name ''quincuncial'' refers to this arrangement: the north pole at the center and quarters of the south pole in the corners form a quincunx pattern like the pips on the ''five'' face of a traditional dice, die. The projection has the distinctive property that it forms a seamless square tiling of the plane, conformal except at four Mathematical singularity, singular points along the equator. Typically the projection is square and oriented such that the north pole lies at the center, but Guyou hemisphere-in-a-square projection, an oblique aspect in a rectangle was proposed by Émile Guyou in 1887, and Adams hemisphere-in-a-square_projection, a transverse aspect wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dihedra
A dihedron (pl. dihedra) is a type of polyhedron, made of two polygon faces which share the same set of ''n'' edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is the fundamental domain of a lens space L(''p'',''q''). Dihedra have also been called bihedra, flat polyhedra, or doubly covered polygons. As a spherical tiling, a dihedron can exist as nondegenerate form, with two ''n''-sided faces covering the sphere, each face being a hemisphere, and vertices on a great circle. It is regular if the vertices are equally spaced. The dual of an ''n''-gonal dihedron is an ''n''-gonal hosohedron, where ''n'' digon faces share two vertices. As a flat-faced polyhedron A dihedron can be considered a degenerate prism whose two (planar) ''n''-sided polygon bases are connected "back-to-back", so that the resulting object has no depth. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |