Peirce Quincuncial Projection
The Peirce quincuncial projection is the conformal map projection from the sphere to an unfolded square dihedron, developed by Charles Sanders Peirce in 1879. Each octant projects onto an isosceles right triangle, and these are arranged into a square. The name ''quincuncial'' refers to this arrangement: the north pole at the center and quarters of the south pole in the corners form a quincunx pattern like the pips on the ''five'' face of a traditional die. The projection has the distinctive property that it forms a seamless square tiling of the plane, conformal except at four singular points along the equator. Typically the projection is square and oriented such that the north pole lies at the center, but an oblique aspect in a rectangle was proposed by Émile Guyou in 1887, and a transverse aspect was proposed by Oscar Adams in 1925. The projection has seen use in digital photography for portraying spherical panoramas. History The maturation of complex analysis led to gene ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

Peirce Quincuncial Projection SW 20W
Peirce may refer to: Schools * Peirce College, Philadelphia, formerly known as Peirce College of Business, Peirce Junior College and Peirce School of Business Administration * Peirce School (also known as Old Peirce School), West Newton, Massachusetts * Helen C. Peirce School of International Studies, an elementary school in Chicago Others * Peirce (crater), a lunar crater * Peirce (given name), including a list of people with the given name * Peirce (surname), including a list of people with the surname See also * * * Pierce (other) * Peirse (other) Peirse may refer to: People with the surname *Henry Peirse (1750s-1824), English politician * Richard Peirse (Royal Navy officer) (1860-1940), English Royal Navy officer *Richard Peirse (1892-1970), English RAF commander * Richard Peirse (RAF offic ...

Complex Plane
In mathematics, the complex plane is the plane formed by the complex numbers, with a Cartesian coordinate system such that the -axis, called the real axis, is formed by the real numbers, and the -axis, called the imaginary axis, is formed by the imaginary numbers. The complex plane allows a geometric interpretation of complex numbers. Under addition, they add like vectors. The multiplication of two complex numbers can be expressed more easily in polar coordinates—the magnitude or ''modulus'' of the product is the product of the two absolute values, or moduli, and the angle or ''argument'' of the product is the sum of the two angles, or arguments. In particular, multiplication by a complex number of modulus 1 acts as a rotation. The complex plane is sometimes known as the Argand plane or Gauss plane. Notational conventions Complex numbers In complex analysis, the complex numbers are customarily represented by the symbol ''z'', which can be separated into its real (''x'') and ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

Tessellate
A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called ''tiles'', with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety of geometries. A periodic tiling has a repeating pattern. Some special kinds include '' regular tilings'' with regular polygonal tiles all of the same shape, and '' semiregular tilings'' with regular tiles of more than one shape and with every corner identically arranged. The patterns formed by periodic tilings can be categorized into 17 wallpaper groups. A tiling that lacks a repeating pattern is called "non-periodic". An '' aperiodic tiling'' uses a small set of tile shapes that cannot form a repeating pattern. A '' tessellation of space'', also known as a space filling or honeycomb, can be defined in the geometry of higher dimensions. A real physical tessellation is a tiling made of materials such as cemented ceramic squares or hexagons. ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

Peirce Quincuncial Projection SW 20W Tiles
Peirce may refer to: Schools * Peirce College, Philadelphia, formerly known as Peirce College of Business, Peirce Junior College and Peirce School of Business Administration * Peirce School (also known as Old Peirce School), West Newton, Massachusetts * Helen C. Peirce School of International Studies, an elementary school in Chicago Others * Peirce (crater), a lunar crater * Peirce (given name), including a list of people with the given name * Peirce (surname), including a list of people with the surname See also * * * Pierce (other) * Peirse (other) Peirse may refer to: People with the surname *Henry Peirse (1750s-1824), English politician * Richard Peirse (Royal Navy officer) (1860-1940), English Royal Navy officer *Richard Peirse (1892-1970), English RAF commander * Richard Peirse (RAF offic ...

Differentiability
In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. In other words, the graph of a differentiable function has a non-vertical tangent line at each interior point in its domain. A differentiable function is smooth (the function is locally well approximated as a linear function at each interior point) and does not contain any break, angle, or cusp. If is an interior point in the domain of a function , then is said to be ''differentiable at'' if the derivative f'(x_0) exists. In other words, the graph of has a non-vertical tangent line at the point . is said to be differentiable on if it is differentiable at every point of . is said to be ''continuously differentiable'' if its derivative is also a continuous function over the domain of the function f. Generally speaking, is said to be of class if its first k derivatives f^(x), f^(x), \ldots, f^(x) exist and are continuous over the domain of the func ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

Mercator Projection
The Mercator projection () is a cylindrical map projection presented by Flemish geographer and cartographer Gerardus Mercator in 1569. It became the standard map projection for navigation because it is unique in representing north as up and south as down everywhere while preserving local directions and shapes. The map is thereby conformal. As a side effect, the Mercator projection inflates the size of objects away from the equator. This inflation is very small near the equator but accelerates with increasing latitude to become infinite at the poles. As a result, landmasses such as Greenland, Antarctica and Russia appear far larger than they actually are relative to landmasses near the equator, such as Central Africa. History There is some controversy over the origins of the Mercator. German polymath Erhard Etzlaub engraved miniature "compass maps" (about 10×8 cm) of Europe and parts of Africa that spanned latitudes 0°–67° to allow adjustment of his portable pocket-s ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

Peirce Projection Spherical Conics
Peirce may refer to: Schools * Peirce College, Philadelphia, formerly known as Peirce College of Business, Peirce Junior College and Peirce School of Business Administration * Peirce School (also known as Old Peirce School), West Newton, Massachusetts * Helen C. Peirce School of International Studies, an elementary school in Chicago Others * Peirce (crater), a lunar crater * Peirce (given name), including a list of people with the given name * Peirce (surname), including a list of people with the surname See also * * * Pierce (other) * Peirse (other) Peirse may refer to: People with the surname *Henry Peirse (1750s-1824), English politician * Richard Peirse (Royal Navy officer) (1860-1940), English Royal Navy officer *Richard Peirse (1892-1970), English RAF commander * Richard Peirse (RAF offic ...

Lemniscate Elliptic Functions
In mathematics, the lemniscate elliptic functions are elliptic functions related to the arc length of the lemniscate of Bernoulli. They were first studied by Giulio Fagnano in 1718 and later by Leonhard Euler and Carl Friedrich Gauss, among others. The lemniscate sine and lemniscate cosine functions, usually written with the symbols and (sometimes the symbols and or and are used instead) are analogous to the trigonometric functions sine and cosine. While the trigonometric sine relates the arc length to the chord length in a unit-diameter circle x^2+y^2 = x, the lemniscate sine relates the arc length to the chord length of a lemniscate \bigl(x^2+y^2\bigr)^2=x^2-y^2. The lemniscate functions have periods related to a number called the lemniscate constant, the ratio of a lemniscate's perimeter to its diameter. This number is a quartic analog of the ( quadratic) , ratio of perimeter to diameter of a circle. As complex functions, and have a square period lattice (a mul ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

Jacobi Elliptic Functions
In mathematics, the Jacobi elliptic functions are a set of basic elliptic functions. They are found in the description of the motion of a pendulum (see also pendulum (mathematics)), as well as in the design of electronic elliptic filters. While trigonometry, trigonometric functions are defined with reference to a circle, the Jacobi elliptic functions are a generalization which refer to other conic sections, the ellipse in particular. The relation to trigonometric functions is contained in the notation, for example, by the matching notation \operatorname for \sin. The Jacobi elliptic functions are used more often in practical problems than the Weierstrass elliptic functions as they do not require notions of complex analysis to be defined and/or understood. They were introduced by . Carl Friedrich Gauss had already studied special Jacobi elliptic functions in 1797, the lemniscate elliptic functions in particular, but his work was published much later. Overview There are twelve Jacob ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

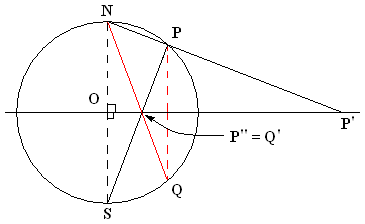
Stereographic Projection
In mathematics, a stereographic projection is a perspective projection of the sphere, through a specific point on the sphere (the ''pole'' or ''center of projection''), onto a plane (geometry), plane (the ''projection plane'') perpendicular to the diameter through the point. It is a smooth function, smooth, bijection, bijective function (mathematics), function from the entire sphere except the center of projection to the entire plane. It maps circle of a sphere, circles on the sphere to generalised circle, circles or lines on the plane, and is conformal map, conformal, meaning that it preserves angles at which curves meet and thus Local property, locally approximately preserves similarity (geometry), shapes. It is neither isometry, isometric (distance preserving) nor Equiareal map, equiareal (area preserving). The stereographic projection gives a way to representation (mathematics), represent a sphere by a plane. The metric tensor, metric induced metric, induced by the inverse s ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

Map Projection
In cartography, map projection is the term used to describe a broad set of transformations employed to represent the two-dimensional curved surface of a globe on a plane. In a map projection, coordinates, often expressed as latitude and longitude, of locations from the surface of the globe are transformed to coordinates on a plane. Projection is a necessary step in creating a two-dimensional map and is one of the essential elements of cartography. All projections of a sphere on a plane necessarily distort the surface in some way and to some extent. Depending on the purpose of the map, some distortions are acceptable and others are not; therefore, different map projections exist in order to preserve some properties of the sphere-like body at the expense of other properties. The study of map projections is primarily about the characterization of their distortions. There is no limit to the number of possible map projections. More generally, projections are considered in several fi ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]