|
Partially Observable Markov Decision Process
A partially observable Markov decision process (POMDP) is a generalization of a Markov decision process (MDP). A POMDP models an agent decision process in which it is assumed that the system dynamics are determined by an MDP, but the agent cannot directly observe the underlying state. Instead, it must maintain a sensor model (the probability distribution of different observations given the underlying state) and the underlying MDP. Unlike the policy function in MDP which maps the underlying states to the actions, POMDP's policy is a mapping from the history of observations (or belief states) to the actions. The POMDP framework is general enough to model a variety of real-world sequential decision processes. Applications include robot navigation problems, machine maintenance, and planning under uncertainty in general. The general framework of Markov decision processes with imperfect information was described by Karl Johan Åström in 1965 in the case of a discrete state space, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Principle Component Analysis
Principal component analysis (PCA) is a popular technique for analyzing large datasets containing a high number of dimensions/features per observation, increasing the interpretability of data while preserving the maximum amount of information, and enabling the visualization of multidimensional data. Formally, PCA is a statistical technique for reducing the dimensionality of a dataset. This is accomplished by linearly transforming the data into a new coordinate system where (most of) the variation in the data can be described with fewer dimensions than the initial data. Many studies use the first two principal components in order to plot the data in two dimensions and to visually identify clusters of closely related data points. Principal component analysis has applications in many fields such as population genetics, microbiome studies, and atmospheric science. The principal components of a collection of points in a real coordinate space are a sequence of p unit vectors, where the i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamic Programming
Dynamic programming is both a mathematical optimization method and a computer programming method. The method was developed by Richard Bellman in the 1950s and has found applications in numerous fields, from aerospace engineering to economics. In both contexts it refers to simplifying a complicated problem by breaking it down into simpler sub-problems in a recursive manner. While some decision problems cannot be taken apart this way, decisions that span several points in time do often break apart recursively. Likewise, in computer science, if a problem can be solved optimally by breaking it into sub-problems and then recursively finding the optimal solutions to the sub-problems, then it is said to have '' optimal substructure''. If sub-problems can be nested recursively inside larger problems, so that dynamic programming methods are applicable, then there is a relation between the value of the larger problem and the values of the sub-problems.Cormen, T. H.; Leiserson, C. E.; Riv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Julia (programming Language)
Julia is a high-level, dynamic programming language. Its features are well suited for numerical analysis and computational science. Distinctive aspects of Julia's design include a type system with parametric polymorphism in a dynamic programming language; with multiple dispatch as its core programming paradigm. Julia supports concurrent, (composable) parallel and distributed computing (with or without using MPI or the built-in corresponding to "OpenMP-style" threads), and direct calling of C and Fortran libraries without glue code. Julia uses a just-in-time (JIT) compiler that is referred to as "just- ahead-of-time" (JAOT) in the Julia community, as Julia compiles all code (by default) to machine code before running it. Julia is garbage-collected, uses eager evaluation, and includes efficient libraries for floating-point calculations, linear algebra, random number generation, and regular expression matching. Many libraries are available, including some (e.g., for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
EXPTIME
In computational complexity theory, the complexity class EXPTIME (sometimes called EXP or DEXPTIME) is the set of all decision problems that are solvable by a deterministic Turing machine in exponential time, i.e., in O(2''p''(''n'')) time, where ''p''(''n'') is a polynomial function of ''n''. EXPTIME is one intuitive class in an exponential hierarchy of complexity classes with increasingly more complex oracles or quantifier alternations. For example, the class 2-EXPTIME is defined similarly to EXPTIME but with a doubly exponential time bound. This can be generalized to higher and higher time bounds. EXPTIME can also be reformulated as the space class APSPACE, the set of all problems that can be solved by an alternating Turing machine in polynomial space. EXPTIME relates to the other basic time and space complexity classes in the following way: P ⊆ NP ⊆ PSPACE ⊆ EXPTIME ⊆ NEXPTIME ⊆ EXPSPACE. Furthemore, by the time hierarchy theorem and the space hierar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parity Game
A parity game is played on a colored directed graph, where each node has been colored by a priority – one of (usually) finitely many natural numbers. Two players, 0 and 1, move a (single, shared) token along the edges of the graph. The owner of the node that the token falls on selects the successor node, resulting in a (possibly infinite) path, called the play. The winner of a finite play is the player whose opponent is unable to move. The winner of an infinite play is determined by the priorities appearing in the play. Typically, player 0 wins an infinite play if the largest priority that occurs infinitely often in the play is even. Player 1 wins otherwise. This explains the word "parity" in the title. Parity games lie in the third level of the Borel hierarchy, and are consequently determined. Games related to parity games were implicitly used in Rabin's proof of decidability of the monadic second-order theory of ''n'' successors ( S2S for ''n'' = 2), where determinacy o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Büchi Automaton
In computer science and automata theory, a deterministic Büchi automaton is a theoretical machine which either accepts or rejects infinite inputs. Such a machine has a set of states and a transition function, which determines which state the machine should move to from its current state when it reads the next input character. Some states are accepting states and one state is the start state. The machine accepts an input if and only if it will pass through an accepting state infinitely many times as it reads the input. A non-deterministic Büchi automaton, later referred to just as a Büchi automaton, has a transition function which may have multiple outputs, leading to many possible paths for the same input; it accepts an infinite input if and only if some possible path is accepting. Deterministic and non-deterministic Büchi automata generalize deterministic finite automata and nondeterministic finite automata to infinite inputs. Each are types of ω-automata. Büchi automata r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Undecidable Problem
In computability theory and computational complexity theory, an undecidable problem is a decision problem for which it is proved to be impossible to construct an algorithm that always leads to a correct yes-or-no answer. The halting problem is an example: it can be proven that there is no algorithm that correctly determines whether arbitrary programs eventually halt when run. Background A decision problem is any arbitrary yes-or-no question on an infinite set of inputs. Because of this, it is traditional to define the decision problem equivalently as the set of inputs for which the problem returns ''yes''. These inputs can be natural numbers, but also other values of some other kind, such as strings of a formal language. Using some encoding, such as a Gödel numbering, the strings can be encoded as natural numbers. Thus, a decision problem informally phrased in terms of a formal language is also equivalent to a set of natural numbers. To keep the formal definition simple, it i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Q-learning
''Q''-learning is a model-free reinforcement learning algorithm to learn the value of an action in a particular state. It does not require a model of the environment (hence "model-free"), and it can handle problems with stochastic transitions and rewards without requiring adaptations. For any finite Markov decision process (FMDP), ''Q''-learning finds an optimal policy in the sense of maximizing the expected value of the total reward over any and all successive steps, starting from the current state. ''Q''-learning can identify an optimal action-selection policy for any given FMDP, given infinite exploration time and a partly-random policy. "Q" refers to the function that the algorithm computes – the expected rewards for an action taken in a given state. Reinforcement learning Reinforcement learning involves an agent, a set of ''states'' , and a set of ''actions'' per state. By performing an action a \in A, the agent transitions from state to state. Executing an action ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Complexity Theory
In theoretical computer science and mathematics, computational complexity theory focuses on classifying computational problems according to their resource usage, and relating these classes to each other. A computational problem is a task solved by a computer. A computation problem is solvable by mechanical application of mathematical steps, such as an algorithm. A problem is regarded as inherently difficult if its solution requires significant resources, whatever the algorithm used. The theory formalizes this intuition, by introducing mathematical models of computation to study these problems and quantifying their computational complexity, i.e., the amount of resources needed to solve them, such as time and storage. Other measures of complexity are also used, such as the amount of communication (used in communication complexity), the number of gates in a circuit (used in circuit complexity) and the number of processors (used in parallel computing). One of the roles of compu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Imperfect Information
In economics, perfect information (sometimes referred to as "no hidden information") is a feature of perfect competition. With perfect information in a market, all consumers and producers have complete and instantaneous knowledge of all market prices, their own utility, and own cost functions. In game theory, a sequential game has perfect information if each player, when making any decision, is perfectly informed of all the events that have previously occurred, including the "initialization event" of the game (e.g. the starting hands of each player in a card game).Archived aGhostarchiveand thWayback Machine Perfect information defined at 0:25, with academic sources and . Perfect information is importantly different from complete information, which implies common knowledge of each player's utility functions, payoffs, strategies and "types". A game with perfect information may or may not have complete information. Games where some aspect of play is ''hidden'' from opponents - ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
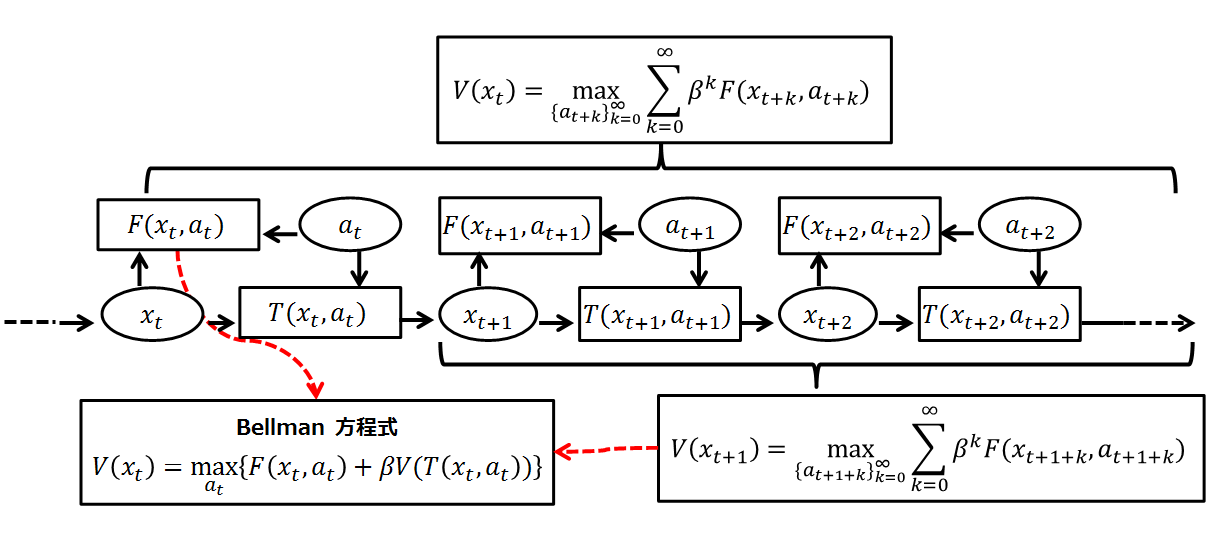
Bellman Equation
A Bellman equation, named after Richard E. Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming. It writes the "value" of a decision problem at a certain point in time in terms of the payoff from some initial choices and the "value" of the remaining decision problem that results from those initial choices. This breaks a dynamic optimization problem into a sequence of simpler subproblems, as Bellman's “principle of optimality" prescribes. The equation applies to algebraic structures with a total ordering; for algebraic structures with a partial ordering, the generic Bellman's equation can be used. The Bellman equation was first applied to engineering control theory and to other topics in applied mathematics, and subsequently became an important tool in economic theory; though the basic concepts of dynamic programming are prefigured in John von Neumann and Oskar Morgenstern's ''Theory of Games and Econ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |