|
P-adic Analytic Group
In mathematics, a pro-''p'' group (for some prime number ''p'') is a profinite group G such that for any open set, open normal subgroup N\triangleleft G the quotient group G/N is a p-group, ''p''-group. Note that, as profinite groups are compact space, compact, the open subgroups are exactly the closed set, closed subgroups of finite index of a subgroup, index, so that the discrete space, discrete quotient group is always finite. Alternatively, one can define a pro-''p'' group to be the inverse limit of an inverse system of discrete finite ''p''-groups. The best-understood (and historically most important) class of pro-''p'' groups is the p-adic number, ''p''-adic analytic groups: groups with the structure of an analytic manifold over \mathbb_p such that group multiplication and inversion are both analytic functions. The work of Alexander Lubotzky, Lubotzky and Mann, combined with Michel Lazard's solution to Hilbert's fifth problem over the ''p''-adic numbers, shows that a pro-''p' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alexander Lubotzky
Alexander Lubotzky ( he, אלכסנדר לובוצקי; born 28 June 1956) is an Israeli mathematician and former politician who is currently a professor at the Weizmann Institute of Science and an adjunct professor at Yale University. He served as a member of the Knesset for The Third Way party between 1996 and 1999. In 2018 he won the Israel Prize for his accomplishments in mathematics and computer science. Biography Alexander (Alex) Lubotzky was born in Tel Aviv to Holocaust survivors. His father, Iser Lubotzky was a Partisan, Irgun officer and the legal advisor of Herut. After school, Lubotzky did his IDF national service as a captain officer in a special intelligence and communication unit. He studied mathematics at Bar-Ilan University during highschool, gaining a BA (summa cum laude) and continuing directly with studying for his PhD under the supervision of Hillel Furstenberg. Lubotzky married Yardenna (daughter of Murray Roston), a lecturer in Art History and English, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topological Groups
In mathematics, topology (from the Greek words , and ) is concerned with the properties of a geometric object that are preserved under continuous deformations, such as stretching, twisting, crumpling, and bending; that is, without closing holes, opening holes, tearing, gluing, or passing through itself. A topological space is a set endowed with a structure, called a ''topology'', which allows defining continuous deformation of subspaces, and, more generally, all kinds of continuity. Euclidean spaces, and, more generally, metric spaces are examples of a topological space, as any distance or metric defines a topology. The deformations that are considered in topology are homeomorphisms and homotopies. A property that is invariant under such deformations is a topological property. Basic examples of topological properties are: the dimension, which allows distinguishing between a line and a surface; compactness, which allows distinguishing between a line and a circle; connec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infinite Group Theory
In abstract algebra, group theory studies the algebraic structures known as group (mathematics), groups. The concept of a group is central to abstract algebra: other well-known algebraic structures, such as ring (mathematics), rings, field (mathematics), fields, and vector spaces, can all be seen as groups endowed with additional operation (mathematics), operations and axioms. Groups recur throughout mathematics, and the methods of group theory have influenced many parts of algebra. Linear algebraic groups and Lie groups are two branches of group theory that have experienced advances and have become subject areas in their own right. Various physical systems, such as crystals and the hydrogen atom, and Standard Model, three of the four known fundamental forces in the universe, may be modelled by symmetry groups. Thus group theory and the closely related representation theory have many important applications in physics, chemistry, and materials science. Group theory is also ce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cambridge University Press
Cambridge University Press is the university press of the University of Cambridge. Granted letters patent by King Henry VIII in 1534, it is the oldest university press in the world. It is also the King's Printer. Cambridge University Press is a department of the University of Cambridge and is both an academic and educational publisher. It became part of Cambridge University Press & Assessment, following a merger with Cambridge Assessment in 2021. With a global sales presence, publishing hubs, and offices in more than 40 countries, it publishes over 50,000 titles by authors from over 100 countries. Its publishing includes more than 380 academic journals, monographs, reference works, school and university textbooks, and English language teaching and learning publications. It also publishes Bibles, runs a bookshop in Cambridge, sells through Amazon, and has a conference venues business in Cambridge at the Pitt Building and the Sir Geoffrey Cass Sports and Social Centre. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Profinite Group
In mathematics, a profinite group is a topological group that is in a certain sense assembled from a system of finite groups. The idea of using a profinite group is to provide a "uniform", or "synoptic", view of an entire system of finite groups. Properties of the profinite group are generally speaking uniform properties of the system. For example, the profinite group is finitely generated (as a topological group) if and only if there exists d\in\N such that every group in the system can be generated by d elements. Many theorems about finite groups can be readily generalised to profinite groups; examples are Lagrange's theorem and the Sylow theorems. To construct a profinite group one needs a system of finite groups and group homomorphisms between them. Without loss of generality, these homomorphisms can be assumed to be surjective, in which case the finite groups will appear as quotient groups of the resulting profinite group; in a sense, these quotients approximate the profi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Residual Property (mathematics)
In the mathematical field of group theory, a group is residually ''X'' (where ''X'' is some property of groups) if it "can be recovered from groups with property ''X''". Formally, a group ''G'' is residually ''X'' if for every non-trivial element ''g'' there is a homomorphism ''h'' from ''G'' to a group with property ''X'' such that h(g)\neq e. More categorically, a group is residually ''X'' if it embeds into its pro-''X'' completion (see profinite group, pro-p group), that is, the inverse limit of the inverse system consisting of all morphisms \phi\colon G \to H from ''G'' to some group ''H'' with property ''X''. Examples Important examples include: * Residually finite * Residually nilpotent In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n, called the index (or sometimes the degree), such that x^n=0. The term was introduced by Benjamin Peirce in the context of his work on the cla ... * Residually solvable * Residually ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Identity Matrix
In linear algebra, the identity matrix of size n is the n\times n square matrix with ones on the main diagonal and zeros elsewhere. Terminology and notation The identity matrix is often denoted by I_n, or simply by I if the size is immaterial or can be trivially determined by the context. I_1 = \begin 1 \end ,\ I_2 = \begin 1 & 0 \\ 0 & 1 \end ,\ I_3 = \begin 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end ,\ \dots ,\ I_n = \begin 1 & 0 & 0 & \cdots & 0 \\ 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & 1 \end. The term unit matrix has also been widely used, but the term ''identity matrix'' is now standard. The term ''unit matrix'' is ambiguous, because it is also used for a matrix of ones and for any unit of the ring of all n\times n matrices. In some fields, such as group theory or quantum mechanics, the identity matrix is sometimes denoted by a boldface one, \mathbf, or called "id" (short for identity) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix (mathematics)
In mathematics, a matrix (plural matrices) is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns, which is used to represent a mathematical object or a property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two by three matrix", a "-matrix", or a matrix of dimension . Without further specifications, matrices represent linear maps, and allow explicit computations in linear algebra. Therefore, the study of matrices is a large part of linear algebra, and most properties and operations of abstract linear algebra can be expressed in terms of matrices. For example, matrix multiplication represents composition of linear maps. Not all matrices are related to linear algebra. This is, in particular, the case in graph theory, of incidence matrices, and adjacency matrices. ''This article focuses on matrices related to linear algebra, and, un ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
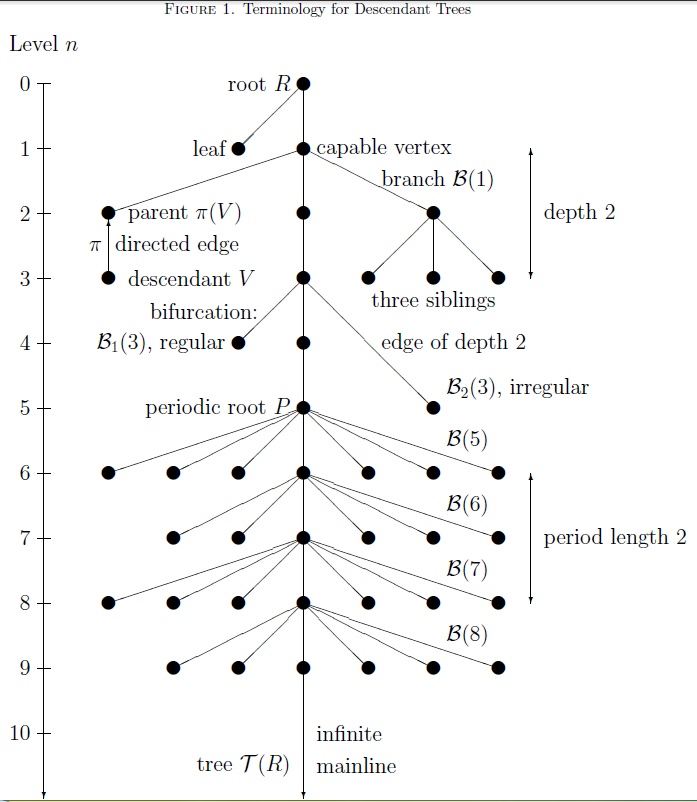
Descendant Tree (group Theory)
In mathematics, specifically group theory, a descendant tree is a hierarchical structure that visualizes parent-descendant relations between isomorphism classes of finite groups of prime power order p^n, for a fixed prime number p and varying integer exponents n\ge 0. Such groups are briefly called ''finite'' ''p-groups''. The ''vertices'' of a descendant tree are isomorphism classes of finite ''p''-groups. Additionally to their ''order'' p^n, finite ''p''-groups have two further related invariants, the ''nilpotency class'' c and the coclass r=n-c. It turned out that descendant trees of a particular kind, the so-called pruned coclass trees whose infinitely many vertices share a common coclass r, reveal a repeating finite pattern. These two crucial properties of finiteness and periodicity admit a characterization of all members of the tree by finitely many parametrized presentations. Consequently, descendant trees play a fundamental role in the classification of finite ''p''-groups ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prüfer Rank
In mathematics, especially in the area of algebra known as group theory, the Prüfer rank of a pro-p group measures the size of a group in terms of the ranks of its elementary abelian sections.. The rank is well behaved and helps to define analytic pro-p-groups. The term is named after Heinz Prüfer. Definition The Prüfer rank of pro-p-group G is ::\sup\ where d(H) is the rank of the abelian group :H/\Phi(H), where \Phi(H) is the Frattini subgroup of H. As the Frattini subgroup of H can be thought of as the group of non-generating elements of H, it can be seen that d(H) will be equal to the ''size of any minimal generating set'' of H. Properties Those profinite groups with finite Prüfer rank are more amenable to analysis. Specifically in the case of finitely generated pro-p groups, having finite Prüfer rank is equivalent to having an open normal subgroup that is powerful. In turn these are precisely the class of pro-p groups that are p-adic analytic - that is g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hilbert's Fifth Problem
Hilbert's fifth problem is the fifth mathematical problem from the problem list publicized in 1900 by mathematician David Hilbert, and concerns the characterization of Lie groups. The theory of Lie groups describes continuous symmetry in mathematics; its importance there and in theoretical physics (for example quark theory) grew steadily in the twentieth century. In rough terms, Lie group theory is the common ground of group theory and the theory of topological manifolds. The question Hilbert asked was an acute one of making this precise: is there any difference if a restriction to smooth manifolds is imposed? The expected answer was in the negative (the classical groups, the most central examples in Lie group theory, are smooth manifolds). This was eventually confirmed in the early 1950s. Since the precise notion of "manifold" was not available to Hilbert, there is room for some debate about the formulation of the problem in contemporary mathematical language. Formulation of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |