|
Output-sensitive Algorithm
In computer science, an output-sensitive algorithm is an algorithm whose running time depends on the size of the output, instead of, or in addition to, the size of the input. For certain problems where the output size varies widely, for example from linear in the size of the input to quadratic in the size of the input, analyses that take the output size explicitly into account can produce better runtime bounds that differentiate algorithms that would otherwise have identical asymptotic complexity. Examples Division by subtraction A simple example of an output-sensitive algorithm is given by the division algorithm ''division by subtraction'' which computes the quotient and remainder of dividing two positive integers using only addition, subtraction, and comparisons: def divide(number: int, divisor: int) -> tuple nt, int """Division by subtraction.""" if divisor 0: raise ZeroDivisionError if number >> divide(10, 2) (5, 0) >>> divide(10, 3) (3, 1) This al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Computer Science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, applied disciplines (including the design and implementation of Computer architecture, hardware and Software engineering, software). Algorithms and data structures are central to computer science. The theory of computation concerns abstract models of computation and general classes of computational problem, problems that can be solved using them. The fields of cryptography and computer security involve studying the means for secure communication and preventing security vulnerabilities. Computer graphics (computer science), Computer graphics and computational geometry address the generation of images. Programming language theory considers different ways to describe computational processes, and database theory concerns the management of re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Lazy Evaluation
In programming language theory, lazy evaluation, or call-by-need, is an evaluation strategy which delays the evaluation of an Expression (computer science), expression until its value is needed (non-strict evaluation) and which avoids repeated evaluations (by the use of Sharing (computer science), sharing). The benefits of lazy evaluation include: * The ability to define control flow (structures) as abstractions instead of Language primitive, primitives. * The ability to define actual infinity, potentially infinite data structures. This allows for more straightforward implementation of some algorithms. * The ability to define partly-defined data structures where some elements are errors. This allows for rapid prototyping. Lazy evaluation is often combined with memoization, as described in Jon Bentley (computer scientist), Jon Bentley's ''Writing Efficient Programs''. After a function's value is computed for that Parameter (computer programming), parameter or set of parameters, th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Enumeration Algorithm
In computer science, an enumeration algorithm is an algorithm that enumerates the answers to a computational problem. Formally, such an algorithm applies to problems that take an input and produce a list of solutions, similarly to function problems. For each input, the enumeration algorithm must produce the list of all solutions, without duplicates, and then halt. The performance of an enumeration algorithm is measured in terms of the time required to produce the solutions, either in terms of the total time required to produce all solutions, or in terms of the maximal delay between two consecutive solutions and in terms of a preprocessing time, counted as the time before outputting the first solution. This complexity can be expressed in terms of the size of the input, the size of each individual output, or the total size of the set of all outputs, similarly to what is done with output-sensitive algorithms. Formal definitions An enumeration problem P is defined as a relation R o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Voronoi Diagram
In mathematics, a Voronoi diagram is a partition of a plane into regions close to each of a given set of objects. It can be classified also as a tessellation. In the simplest case, these objects are just finitely many points in the plane (called seeds, sites, or generators). For each seed there is a corresponding region, called a Voronoi cell, consisting of all points of the plane closer to that seed than to any other. The Voronoi diagram of a set of points is dual to that set's Delaunay triangulation. The Voronoi diagram is named after mathematician Georgy Voronoy, and is also called a Voronoi tessellation, a Voronoi decomposition, a Voronoi partition, or a Dirichlet tessellation (after Peter Gustav Lejeune Dirichlet). Voronoi cells are also known as Thiessen polygons, after Alfred H. Thiessen. Voronoi diagrams have practical and theoretical applications in many fields, mainly in science and technology, but also in visual art. Simplest case In the simplest case, shown in the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Range Filter
Range may refer to: Geography * Range (geographic), a chain of hills or mountains; a somewhat linear, complex mountainous or hilly area (cordillera, sierra) ** Mountain range, a group of mountains bordered by lowlands * Range, a term used to identify a survey township in the US * Rangeland, deserts, grasslands, shrublands, wetlands, and woodlands that are grazed by domestic livestock or wild animals Mathematics * Range of a function, a set containing the output values produced by a function * Range (statistics), the difference between the highest and the lowest values in a set * Interval (mathematics), also called ''range'', a set of real numbers that includes all numbers between any two numbers in the set * Column space, also called the ''range'' of a matrix, is the set of all possible linear combinations of the column vectors of the matrix * Projective range, a line or a conic in projective geometry * Range of a quantifier, in logic Music * Range (music), the distance f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
ACM Transactions On Graphics
''ACM Transactions on Graphics'' (TOG) is a bimonthly peer-reviewed scientific journal that covers the field of computer graphics. The editor-in-chief is Carol O'Sullivan (Trinity College Dublin). According to the ''Journal Citation Reports'', the journal had a 2023 impact factor of 7.8. The journal ranks 1st in computer graphics publications, according to Google Scholar Metrics. History It was established in 1982 and is published by the Association for Computing Machinery. TOG publishes two special issues for ACM SIGGRAPH's conference proceedings. Starting in 2003, all papers accepted for presentation at the annual SIGGRAPH SIGGRAPH (Special Interest Group on Computer Graphics and Interactive Techniques) is an annual conference centered around computer graphics organized by ACM, starting in 1974 in Boulder, CO. The main conference has always been held in North ... conference are printed in a special summer issue of the journal. Beginning in 2008, papers presented at S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hidden Surface Removal
In 3D computer graphics, hidden-surface determination (also known as shown-surface determination, hidden-surface removal (HSR), occlusion culling (OC) or visible-surface determination (VSD)) is the process of identifying what surfaces and parts of surfaces can be seen from a particular viewing angle. A hidden-surface determination algorithm is a solution to the visibility problem, which was one of the first major problems in the field of 3D computer graphics. The process of hidden-surface determination is sometimes called hiding, and such an algorithm is sometimes called a hider. When referring to line rendering it is known as hidden-line removal. Hidden-surface determination is necessary to render a scene correctly, so that one may not view features hidden behind the model itself, allowing only the naturally viewable portion of the graphic to be visible. Background Hidden-surface determination is a process that identifies which surfaces are not visible to the user (for example, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
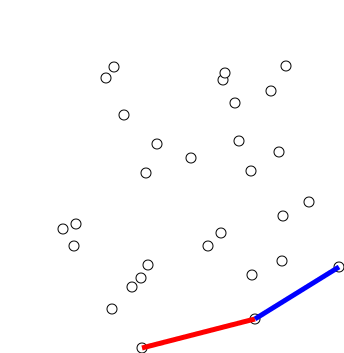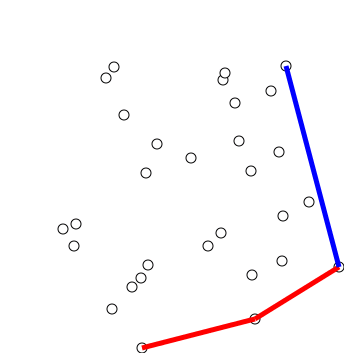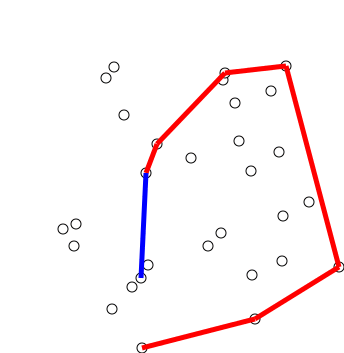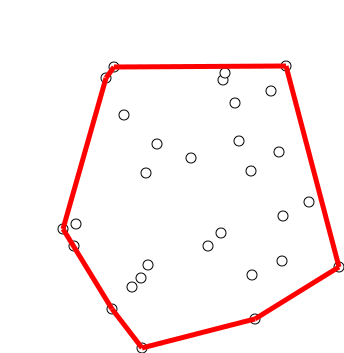
Chan's Algorithm
In computational geometry, Chan's algorithm, named after Timothy M. Chan, is an optimal output-sensitive algorithm to compute the convex hull of a set P of n points, in 2- or 3-dimensional space. The algorithm takes O(n \log h) time, where h is the number of vertices of the output (the convex hull). In the planar case, the algorithm combines an O(n \log n) algorithm ( Graham scan, for example) with Jarvis march (O(nh)), in order to obtain an optimal O(n \log h) time. Chan's algorithm is notable because it is much simpler than the Kirkpatrick–Seidel algorithm, and it naturally extends to 3-dimensional space. This paradigm has been independently developed by Frank Nielsen in his Ph.D. thesis. Algorithm Overview A single pass of the algorithm requires a parameter m which is between 0 and n (number of points of our set P). Ideally, m = h but h, the number of vertices in the output convex hull, is not known at the start. Multiple passes with increasing values of m are done whi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Algorithm
In mathematics and computer science, an algorithm () is a finite sequence of Rigour#Mathematics, mathematically rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algorithms are used as specifications for performing calculations and data processing. More advanced algorithms can use Conditional (computer programming), conditionals to divert the code execution through various routes (referred to as automated decision-making) and deduce valid inferences (referred to as automated reasoning). In contrast, a Heuristic (computer science), heuristic is an approach to solving problems without well-defined correct or optimal results.David A. Grossman, Ophir Frieder, ''Information Retrieval: Algorithms and Heuristics'', 2nd edition, 2004, For example, although social media recommender systems are commonly called "algorithms", they actually rely on heuristics as there is no truly "correct" recommendation. As an e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Ultimate Convex Hull Algorithm
Ultimate or Ultimates may refer to: Arts, entertainment, and media Music Albums * ''Ultimate'' (Bryan Adams album) * ''Ultimate'' (Jolin Tsai album) * ''Ultimate'' (Pet Shop Boys album) *''Ultimate!'', an album by The Yardbirds *'' Ultimate Prince'' or just Ultimate, an album by Prince Songs * "Ultimate" (song), by Denzel Curry, 2015 *"Ultimate", a song by Lindsay Lohan from the ''Freaky Friday'' soundtrack Video games *''Super Smash Bros. Ultimate'', often referred to as simply ''Ultimate''. *''Ultimate General'', a series of computer games recreating the American Civil War *Ultimate Play the Game or just Ultimate, a video game developer, now known as Rare Other uses in arts, entertainment, and media *Ultimate (roller coaster), at Lightwater Valley amusement park near Ripon, North Yorkshire, England *Ultimates, a fictional superhero group in the Marvel Comics universe Philosophy *The Ultimate (philosophy), the concept of an unconditional reality in metaphysics or theology ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Graham Scan
Graham's scan is a method of finding the convex hull of a finite set of points in the plane with time complexity O(''n'' log ''n''). It is named after Ronald Graham, who published the original algorithm in 1972. The algorithm finds all vertices of the convex hull ordered along its boundary. It uses a stack to detect and remove concavities in the boundary efficiently. Algorithm The first step in this algorithm is to find the point with the lowest y-coordinate. If the lowest y-coordinate exists in more than one point in the set, the point with the lowest x-coordinate out of the candidates should be chosen. Call this point ''P''. This step takes O(''n''), where ''n'' is the number of points in question. Next, the set of points must be sorted in increasing order of the angle they and the point ''P'' make with the x-axis. Any general-purpose sorting algorithm is appropriate for this, for example heapsort (which is O(''n'' log ''n'')). Sorting in order of angle does not require ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |