|
Online Mirror Descent
In mathematics, mirror descent is an iterative optimization algorithm for finding a local minimum of a differentiable function. It generalizes algorithms such as gradient descent and multiplicative weights. History Mirror descent was originally proposed by Nemirovski and Yudin in 1983. Motivation In gradient descent with the sequence of learning rates (\eta_n)_ applied to a differentiable function F, one starts with a guess \mathbf_0 for a local minimum of F, and considers the sequence \mathbf_0, \mathbf_1, \mathbf_2, \ldots such that :\mathbf_=\mathbf_n-\eta_n \nabla F(\mathbf_n),\ n \ge 0. This can be reformulated by noting that :\mathbf_=\arg \min_ \left(F(\mathbf_n) + \nabla F(\mathbf_n)^T (\mathbf - \mathbf_n) + \frac\, \mathbf - \mathbf_n\, ^2\right) In other words, \mathbf_ minimizes the first-order approximation to F at \mathbf_n with added proximity term \, \mathbf - \mathbf_n\, ^2. This Euclidean distance term is a particular example of a Bregman distance. Us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Iterative Algorithm
In computational mathematics, an iterative method is a mathematical procedure that uses an initial value to generate a sequence of improving approximate solutions for a class of problems, in which the ''n''-th approximation is derived from the previous ones. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method. An iterative method is called convergent if the corresponding sequence converges for given initial approximations. A mathematically rigorous convergence analysis of an iterative method is usually performed; however, heuristic-based iterative methods are also common. In contrast, direct methods attempt to solve the problem by a finite sequence of operations. In the absence of rounding errors, direct methods would deliver an exact solution (for example, solving a linear system of equations A\mathbf=\mathbf by Gaussian elimination). Iterative methods are often the only choice for nonlinear equations. Howe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems of sorts arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries. In the more general approach, an optimization problem consists of maxima and minima, maximizing or minimizing a Function of a real variable, real function by systematically choosing Argument of a function, input values from within an allowed set and computing the Value (mathematics), value of the function. The generalization of optimization theory and techniques to other formulations constitutes a large area of applied mathematics. More generally, opti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algorithm
In mathematics and computer science, an algorithm () is a finite sequence of rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algorithms are used as specifications for performing calculations and data processing. More advanced algorithms can perform automated deductions (referred to as automated reasoning) and use mathematical and logical tests to divert the code execution through various routes (referred to as automated decision-making). Using human characteristics as descriptors of machines in metaphorical ways was already practiced by Alan Turing with terms such as "memory", "search" and "stimulus". In contrast, a Heuristic (computer science), heuristic is an approach to problem solving that may not be fully specified or may not guarantee correct or optimal results, especially in problem domains where there is no well-defined correct or optimal result. As an effective method, an algorithm ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Local Minimum
In mathematical analysis, the maxima and minima (the respective plurals of maximum and minimum) of a function, known collectively as extrema (the plural of extremum), are the largest and smallest value of the function, either within a given range (the ''local'' or ''relative'' extrema), or on the entire domain (the ''global'' or ''absolute'' extrema). Pierre de Fermat was one of the first mathematicians to propose a general technique, adequality, for finding the maxima and minima of functions. As defined in set theory, the maximum and minimum of a set are the greatest and least elements in the set, respectively. Unbounded infinite sets, such as the set of real numbers, have no minimum or maximum. Definition A real-valued function ''f'' defined on a domain ''X'' has a global (or absolute) maximum point at ''x''∗, if for all ''x'' in ''X''. Similarly, the function has a global (or absolute) minimum point at ''x''∗, if for all ''x'' in ''X''. The value of the function at a m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differentiable Function
In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. In other words, the graph of a differentiable function has a non-vertical tangent line at each interior point in its domain. A differentiable function is smooth (the function is locally well approximated as a linear function at each interior point) and does not contain any break, angle, or cusp. If is an interior point in the domain of a function , then is said to be ''differentiable at'' if the derivative f'(x_0) exists. In other words, the graph of has a non-vertical tangent line at the point . is said to be differentiable on if it is differentiable at every point of . is said to be ''continuously differentiable'' if its derivative is also a continuous function over the domain of the function f. Generally speaking, is said to be of class if its first k derivatives f^(x), f^(x), \ldots, f^(x) exist and are continuous over the domain of the func ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gradient Descent
In mathematics, gradient descent (also often called steepest descent) is a first-order iterative optimization algorithm for finding a local minimum of a differentiable function. The idea is to take repeated steps in the opposite direction of the gradient (or approximate gradient) of the function at the current point, because this is the direction of steepest descent. Conversely, stepping in the direction of the gradient will lead to a local maximum of that function; the procedure is then known as gradient ascent. Gradient descent is generally attributed to Augustin-Louis Cauchy, who first suggested it in 1847. Jacques Hadamard independently proposed a similar method in 1907. Its convergence properties for non-linear optimization problems were first studied by Haskell Curry in 1944, with the method becoming increasingly well-studied and used in the following decades. Description Gradient descent is based on the observation that if the multi-variable function F(\mathbf) is def ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arkadi Nemirovsky
Arkadi Nemirovski (born March 14, 1947) is a professor at the H. Milton Stewart School of Industrial and Systems Engineering at the Georgia Institute of Technology. He has been a leader in continuous optimization and is best known for his work on the ellipsoid method, modern interior-point methods and robust optimization. Biography Nemirovski earned a Ph.D. in Mathematics in 1974 from Moscow State University and a Doctor of Sciences in Mathematics degree in 1990 from the Institute of Cybernetics of the Ukrainian Academy of Sciences in Kiev. He has won three prestigious prizes: the Fulkerson Prize, the George B. Dantzig Prize, and the John von Neumann Theory Prize. He was elected a member of the U.S. National Academy of Engineering (NAE) in 2017 "for the development of efficient algorithms for large-scale convex optimization problems", and the U.S National Academy of Sciences (NAS) in 2020. Academic work Nemirovski first proposed mirror descent along with David Yudin in 1983. H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
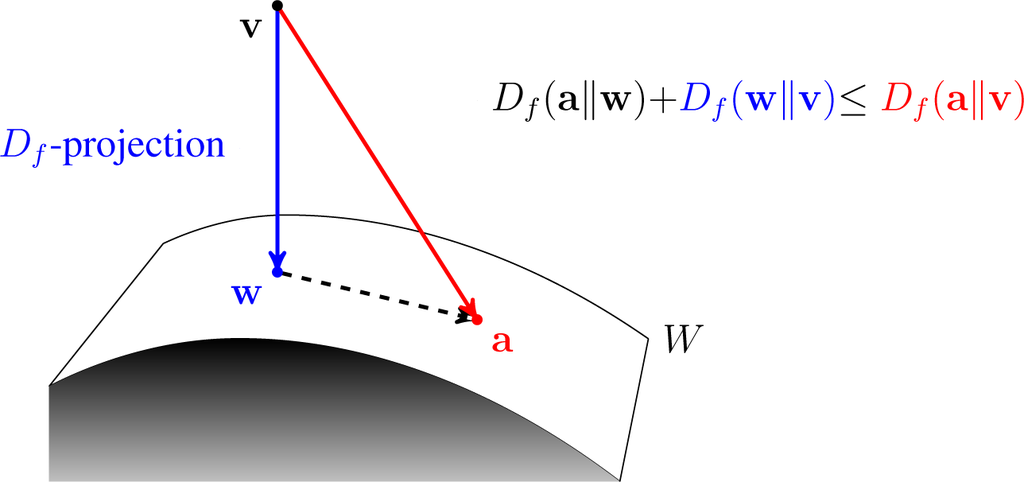
Bregman Distance
In mathematics, specifically statistics and information geometry, a Bregman divergence or Bregman distance is a measure of difference between two points, defined in terms of a strictly convex function; they form an important class of divergences. When the points are interpreted as probability distributions – notably as either values of the parameter of a parametric model or as a data set of observed values – the resulting distance is a statistical distance. The most basic Bregman divergence is the squared Euclidean distance. Bregman divergences are similar to metrics, but satisfy neither the triangle inequality (ever) nor symmetry (in general). However, they satisfy a generalization of the Pythagorean theorem, and in information geometry the corresponding statistical manifold is interpreted as a (dually) flat manifold. This allows many techniques of optimization theory to be generalized to Bregman divergences, geometrically as generalizations of least squares. Bregman divergenc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Function
In mathematics, a real-valued function is called convex if the line segment between any two points on the graph of a function, graph of the function lies above the graph between the two points. Equivalently, a function is convex if its epigraph (mathematics), epigraph (the set of points on or above the graph of the function) is a convex set. A twice-differentiable function of a single variable is convex if and only if its second derivative is nonnegative on its entire domain. Well-known examples of convex functions of a single variable include the quadratic function x^2 and the exponential function e^x. In simple terms, a convex function refers to a function whose graph is shaped like a cup \cup, while a concave function's graph is shaped like a cap \cap. Convex functions play an important role in many areas of mathematics. They are especially important in the study of optimization problems where they are distinguished by a number of convenient properties. For instance, a st ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bregman Divergence
In mathematics, specifically statistics and information geometry, a Bregman divergence or Bregman distance is a measure of difference between two points, defined in terms of a strictly convex function; they form an important class of divergences. When the points are interpreted as probability distributions – notably as either values of the parameter of a parametric model or as a data set of observed values – the resulting distance is a statistical distance. The most basic Bregman divergence is the squared Euclidean distance. Bregman divergences are similar to metrics, but satisfy neither the triangle inequality (ever) nor symmetry (in general). However, they satisfy a generalization of the Pythagorean theorem, and in information geometry the corresponding statistical manifold is interpreted as a (dually) flat manifold. This allows many techniques of optimization theory to be generalized to Bregman divergences, geometrically as generalizations of least squares. Bregman divergenc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |