|
Numerical Differentiation
In numerical analysis, numerical differentiation algorithms estimate the derivative of a mathematical function or subroutine using values of the function and perhaps other knowledge about the function. Finite differences The simplest method is to use finite difference approximations. A simple two-point estimation is to compute the slope of a nearby secant line through the points and . Choosing a small number , represents a small change in , and it can be either positive or negative. The slope of this line is \frac. This expression is Newton's difference quotient (also known as a first-order divided difference). The slope of this secant line differs from the slope of the tangent line by an amount that is approximately proportional to . As approaches zero, the slope of the secant line approaches the slope of the tangent line. Therefore, the true derivative of at is the limit of the value of the difference quotient as the secant lines get closer and closer to being a tange ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivative
In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable. The process of finding a derivative is called differentiation. There are multiple different notations for differentiation. '' Leibniz notation'', named after Gottfried Wilhelm Leibniz, is represented as the ratio of two differentials, whereas ''prime notation'' is written by adding a prime mark. Higher order notations represent repeated differentiation, and they are usually denoted in Leib ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
TI-85
The TI-85 is a graphing calculator made by Texas Instruments based on the Zilog Z80 microprocessor. Designed in 1992 as TI's second graphing calculator (the first was the TI-81), it was replaced by the TI-86, which has also been discontinued. The TI-85 was significantly more powerful than the TI-81, as it was designed as a calculator primarily for use in engineering and calculus courses. Texas Instruments had included a version of BASIC on the device to allow programming. Each calculator came with a cable to connect calculators (simply a three-conductor cable with 2.5 mm phone connectors on each end). Another cable known as the TI-Graph Link was also sold, along with appropriate software, to connect the calculator to a personal computer. These cables made it possible to save programs and make backups. The TI-85 calculator is known in the modern era for being used by Sal Khan from Khan Academy in his educational videos. Assembly programs Enthusiasts analyzed mem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Stability
In the mathematical subfield of numerical analysis, numerical stability is a generally desirable property of numerical algorithms. The precise definition of stability depends on the context: one important context is numerical linear algebra, and another is algorithms for solving ordinary and partial differential equations by discrete approximation. In numerical linear algebra, the principal concern is instabilities caused by proximity to singularities of various kinds, such as very small or nearly colliding eigenvalues. On the other hand, in numerical algorithms for differential equations the concern is the growth of round-off errors and/or small fluctuations in initial data which might cause a large deviation of final answer from the exact solution. Some numerical algorithms may damp out the small fluctuations (errors) in the input data; others might magnify such errors. Calculations that can be proven not to magnify approximation errors are called ''numerically stable''. One ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Holomorphic Function
In mathematics, a holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighbourhood of each point in a domain in complex coordinate space . The existence of a complex derivative in a neighbourhood is a very strong condition: It implies that a holomorphic function is infinitely differentiable and locally equal to its own Taylor series (is '' analytic''). Holomorphic functions are the central objects of study in complex analysis. Though the term '' analytic function'' is often used interchangeably with "holomorphic function", the word "analytic" is defined in a broader sense to denote any function (real, complex, or of more general type) that can be written as a convergent power series in a neighbourhood of each point in its domain. That all holomorphic functions are complex analytic functions, and vice versa, is a major theorem in complex analysis. Holomorphic functions are also sometimes referred to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Python (programming Language)
Python is a high-level programming language, high-level, general-purpose programming language. Its design philosophy emphasizes code readability with the use of significant indentation. Python is type system#DYNAMIC, dynamically type-checked and garbage collection (computer science), garbage-collected. It supports multiple programming paradigms, including structured programming, structured (particularly procedural programming, procedural), object-oriented and functional programming. It is often described as a "batteries included" language due to its comprehensive standard library. Guido van Rossum began working on Python in the late 1980s as a successor to the ABC (programming language), ABC programming language, and he first released it in 1991 as Python 0.9.0. Python 2.0 was released in 2000. Python 3.0, released in 2008, was a major revision not completely backward-compatible with earlier versions. Python 2.7.18, released in 2020, was the last release of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Volatile Variable
In computer programming, a variable is said to be ''volatile'' if its value can be read or modified asynchronously by something other than the current thread of execution. The value of a volatile variable may spontaneously change for reasons such as: sharing values with other threads; sharing values with asynchronous signal handlers; accessing hardware devices via memory-mapped I/O (where you can send and receive messages from peripheral devices by reading from and writing to memory). Support for these use cases varies considerably among the programming languages that have the volatile keyword. Volatility can have implications regarding function calling conventions and how variables are stored, accessed and cached. In C and C++ In C and C++, volatile is a type qualifier, like const, and is a part of a type (e.g. the type of a variable or field). The behavior of the volatile keyword in C and C++ is sometimes given in terms of suppressing optimizations of an optimizing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
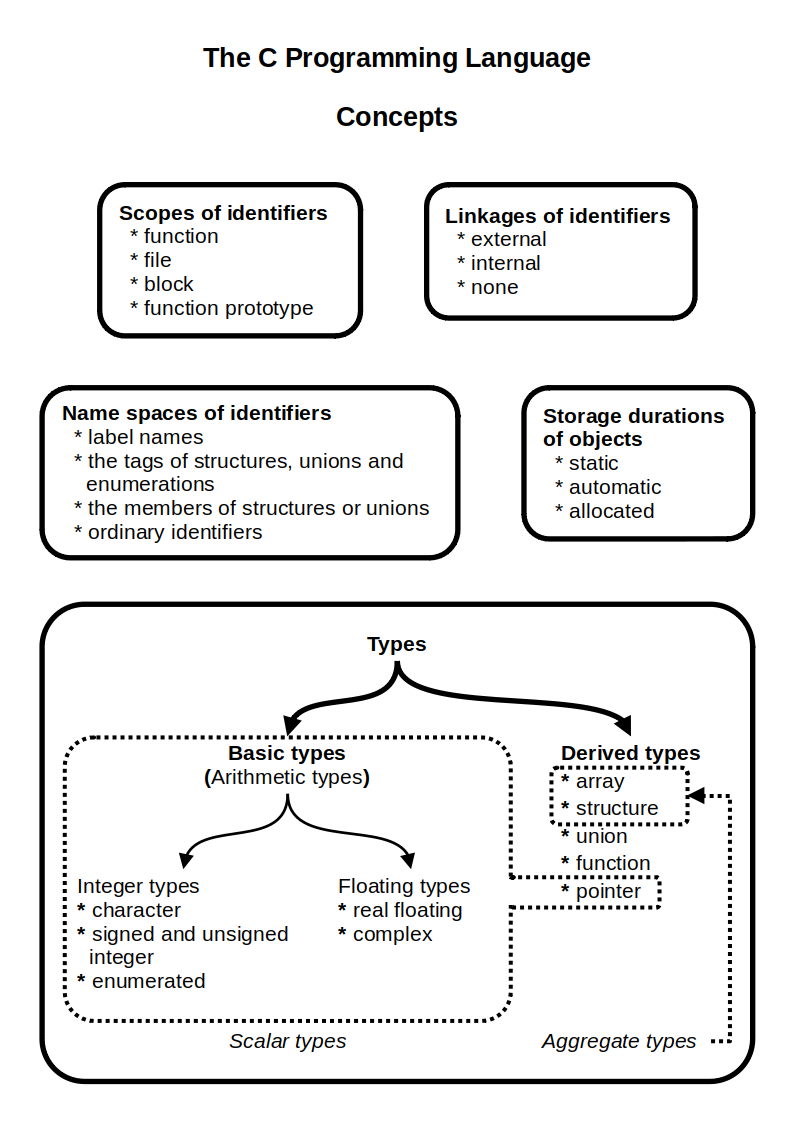
C (programming Language)
C (''pronounced'' '' – like the letter c'') is a general-purpose programming language. It was created in the 1970s by Dennis Ritchie and remains very widely used and influential. By design, C's features cleanly reflect the capabilities of the targeted Central processing unit, CPUs. It has found lasting use in operating systems code (especially in Kernel (operating system), kernels), device drivers, and protocol stacks, but its use in application software has been decreasing. C is commonly used on computer architectures that range from the largest supercomputers to the smallest microcontrollers and embedded systems. A successor to the programming language B (programming language), B, C was originally developed at Bell Labs by Ritchie between 1972 and 1973 to construct utilities running on Unix. It was applied to re-implementing the kernel of the Unix operating system. During the 1980s, C gradually gained popularity. It has become one of the most widely used programming langu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compiler Optimization
An optimizing compiler is a compiler designed to generate code that is optimized in aspects such as minimizing program execution time, memory usage, storage size, and power consumption. Optimization is generally implemented as a sequence of optimizing transformations, a.k.a. compiler optimizations algorithms that transform code to produce semantically equivalent code optimized for some aspect. Optimization is limited by a number of factors. Theoretical analysis indicates that some optimization problems are NP-complete, or even undecidable. Also, producing perfectly ''optimal'' code is not possible since optimizing for one aspect often degrades performance for another. Optimization is a collection of heuristic methods for improving resource usage in typical programs. Categorization Local vs. global scope Scope describes how much of the input code is considered to apply optimizations. Local scope optimizations use information local to a basic block. Since basic blocks cont ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Representable Floating-point Number
In computing, floating-point arithmetic (FP) is arithmetic on subsets of real numbers formed by a ''significand'' (a signed sequence of a fixed number of digits in some base) multiplied by an integer power of that base. Numbers of this form are called floating-point numbers. For example, the number 2469/200 is a floating-point number in base ten with five digits: 2469/200 = 12.345 = \! \underbrace_\text \! \times \! \underbrace_\text\!\!\!\!\!\!\!\overbrace^ However, 7716/625 = 12.3456 is not a floating-point number in base ten with five digits—it needs six digits. The nearest floating-point number with only five digits is 12.346. And 1/3 = 0.3333… is not a floating-point number in base ten with any finite number of digits. In practice, most floating-point systems use base two, though base ten (decimal floating point) is also common. Floating-point arithmetic operations, such as addition and division, approximate the corresponding real number arithmetic operations ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Recipes
''Numerical Recipes'' is the generic title of a series of books on algorithm In mathematics and computer science, an algorithm () is a finite sequence of Rigour#Mathematics, mathematically rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algo ...s and numerical analysis by William H. Press, Saul A. Teukolsky, William T. Vetterling and Brian P. Flannery. In various editions, the books have been in print since 1986. The most recent edition was published in 2007. Overview The ''Numerical Recipes'' books cover a range of topics that include both classical numerical analysis (interpolation, Numerical integration, integration, linear algebra, differential equations, and so on), signal processing (Fast Fourier transform, Fourier methods, Digital filter, filtering), statistical treatment of data, and a few topics in machine learning (hidden Markov model, support vector machines). The writing style is acc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Double Precision
Double-precision floating-point format (sometimes called FP64 or float64) is a floating-point arithmetic, floating-point computer number format, number format, usually occupying 64 Bit, bits in computer memory; it represents a wide range of numeric values by using a floating radix point. Double precision may be chosen when the range or precision of single-precision floating-point format, single precision would be insufficient. In the IEEE 754 standardization, standard, the 64-bit base-2 format is officially referred to as binary64; it was called double in IEEE 754-1985. IEEE 754 specifies additional floating-point formats, including 32-bit base-2 ''single precision'' and, more recently, base-10 representations (decimal floating point). One of the first programming languages to provide floating-point data types was Fortran. Before the widespread adoption of IEEE 754-1985, the representation and properties of floating-point data types depended on the computer manufacturer and compu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Machine Epsilon
Machine epsilon or machine precision is an upper bound on the relative approximation error due to rounding in floating point number systems. This value characterizes computer arithmetic in the field of numerical analysis, and by extension in the subject of computational science. The quantity is also called macheps and it has the symbols Greek epsilon \varepsilon. There are two prevailing definitions, denoted here as ''rounding machine epsilon'' or the ''formal definition'' and ''interval machine epsilon'' or ''mainstream definition''. In the ''mainstream definition'', machine epsilon is independent of rounding method, and is defined simply as ''the difference between 1 and the next larger floating point number''. In the ''formal definition'', machine epsilon is dependent on the type of rounding used and is also called unit roundoff, which has the symbol bold Roman u. The two terms can generally be considered to differ by simply a factor of two, with the ''formal definition'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |