|
Normal Height
Normal heights is a type of height above sea level introduced by Mikhail Molodenskii. The normal height H^* (or H^N) of a point is computed as the ratio of a point's geopotential number (i.e. its geopotential difference with that of sea level), by the average, normal gravity computed along the plumb line of the point. (More precisely, along the ellipsoidal normal, averaging over the height range from 0 — on the reference ellipsoid — to H^*; the procedure is thus recursive.) Normal heights are thus dependent upon the reference ellipsoid chosen. The Soviet Union and many other Eastern European countries have chosen a height system based on normal heights, determined by geodetic precise levelling. Normal gravity values are easy to compute and "hypothesis-free", i.e., one does not have to know, as one would for computing orthometric heights, the density of the Earth's crust around the plumb line. The reference surface that normal heights are measured from is called the quasi-g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Above Sea Level
Height above mean sea level is a measure of the vertical distance (height, elevation or altitude) of a location in reference to a historic mean sea level taken as a vertical datum. In geodesy, it is formalized as '' orthometric heights''. The combination of unit of measurement and the physical quantity (height) is called " metres above mean sea level" in the metric system, while in United States customary and imperial units it would be called " feet above mean sea level". Mean sea levels are affected by climate change and other factors and change over time. For this and other reasons, recorded measurements of elevation above sea level at a reference time in history might differ from the actual elevation of a given location over sea level at a given moment. Uses Metres above sea level is the standard measurement of the elevation or altitude of: * Geographic locations such as towns, mountains and other landmarks. * The top of buildings and other structures. * Flying obje ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mikhail Molodenskii
Mikhail Sergeevich Molodenskii (russian: Михаил Серге́евич Молоденский, – November 12, 1991) was a Soviet physical geodesist. He was once said to be "probably the only geodesist who would have deserved a Nobel prize". He graduated from Moscow State University (1936), since 1946 he worked for the ''Institute of Earth Physics'' (Институт Физики Земли АН СССР). He created an original theory for determining the figure of the Earth and its gravity field based on measurements done on the topographic surface, built the first Soviet gravimeter, developed a theory of the nutation of Earth. He won the Stalin Prize (1946 and 1951) and the Lenin Prize (1961). His legacy includes the Molodensky transformations, which are commonly used to transform between geodetic datums. His main work (since 1932) was on the geoid and its exterior gravity field or geopotential. His aim was to develop hypothesis-free methods for determining both the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geopotential Number
Geopotential is the potential of the Earth's gravity field. For convenience it is often defined as the ''negative'' of the potential energy per unit mass, so that the gravity vector is obtained as the gradient of this potential, without the negation. In addition to the actual potential (the geopotential), a hypothetical normal potential and their difference, the disturbing potential, can also be defined. Concept For geophysical applications, gravity is distinguished from gravitation. Gravity is defined as the resultant force of gravitation and the centrifugal force caused by the Earth's rotation. Likewise, the respective scalar potentials can be added to form an effective potential called the geopotential, W. Global mean sea surface is close to one of the isosurfaces of the geopotential. This ''equipotential surface'', or surface of constant geopotential, is called the ''geoid''. How the gravitational force and the centrifugal force add up to a force orthogonal to the geoid is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Gravity
In geodesy and geophysics, theoretical gravity or normal gravity is an approximation of the true gravity on Earth's surface by means of a mathematical model representing Earth. The most common model of a smoothed Earth is a rotating Earth ellipsoid of revolution (i.e., a spheroid). Principles The type of gravity model used for the Earth depends upon the degree of fidelity required for a given problem. For many problems such as aircraft simulation, it may be sufficient to consider gravity to be a constant, defined as: :g=g_= based upon data from ''World Geodetic System 1984'' ( WGS-84), where g is understood to be pointing 'down' in the local frame of reference. If it is desirable to model an object's weight on Earth as a function of latitude, one could use the following: :g=g_ - \tfrac(g_-g_) \cos\left(2\, \varphi \cdot \frac\right) where * g_ = * g_ = * g_ = * \varphi = latitude, between −90° and +90° Neither of these accounts for changes in gravity with changes in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plumb Line
A plumb bob, plumb bob level, or plummet, is a weight, usually with a pointed tip on the bottom, suspended from a string and used as a vertical reference line, or plumb-line. It is a precursor to the spirit level and used to establish a vertical datum. It is typically made of stone, wood, or lead, but can also be made of other metals. If it is used for decoration, it may be made of bone or ivory. The instrument has been used since at least the time of ancient EgyptDenys A. Stocks. Experiments in Egyptian archaeology: stoneworking technology in ncient Egypt'. Routledge; 2003. . p. 180. to ensure that constructions are " plumb", or vertical. It is also used in surveying, to establish the nadir with respect to gravity of a point in space. It is used with a variety of instruments (including levels, theodolites, and steel tapes) to set the instrument exactly over a fixed survey marker or to transcribe positions onto the ground for placing a marker. Etymology The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ellipsoidal Normal
The ''n''-vector representation (also called geodetic normal or ellipsoid normal vector) is a three-parameter non-singular representation well-suited for replacing geodetic coordinates (latitude and longitude) for horizontal position representation in mathematical calculations and computer algorithms. Geometrically, the ''n''-vector for a given position on an ellipsoid is the outward-pointing unit vector that is normal in that position to the ellipsoid. For representing horizontal positions on Earth, the ellipsoid is a reference ellipsoid and the vector is decomposed in an Earth-centered Earth-fixed coordinate system. It behaves smoothly at all Earth positions, and it holds the mathematical one-to-one property. More in general, the concept can be applied to representing positions on the boundary of a strictly convex bounded subset of ''k''-dimensional Euclidean space, provided that that boundary is a differentiable manifold. In this general case, the ''n''-vector consists ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reference Ellipsoid
An Earth ellipsoid or Earth spheroid is a mathematical figure approximating the Earth's form, used as a reference frame for computations in geodesy, astronomy, and the geosciences. Various different ellipsoids have been used as approximations. It is a spheroid (an ellipsoid of revolution) whose minor axis (shorter diameter), which connects the geographical North Pole and South Pole, is approximately aligned with the Earth's axis of rotation. The ellipsoid is defined by the ''equatorial axis'' (''a'') and the ''polar axis'' (''b''); their radial difference is slightly more than 21 km, or 0.335% of ''a'' (which is not quite 6,400 km). Many methods exist for determination of the axes of an Earth ellipsoid, ranging from meridian arcs up to modern satellite geodesy or the analysis and interconnection of continental geodetic networks. Amongst the different set of data used in national surveys are several of special importance: the Bessel ellipsoid of 1841, the internatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthometric Height
The orthometric height is the vertical distance ''H'' along the plumb line from a point of interest to a reference surface known as the ''geoid'', the vertical datum that approximates mean sea level. Orthometric height is one of the scientific formalizations of a laypersons' "height above sea level", along with other types of heights in Geodesy. In the US, the current NAVD88 datum is tied to a defined elevation at one point rather than to any location's exact mean sea level. Orthometric heights are usually used in the US for engineering work, although dynamic height may be chosen for large-scale hydrological purposes. Heights for measured points are shown on National Geodetic Survey data sheets, data that was gathered over many decades by precise spirit leveling over thousands of miles. Alternatives to orthometric height include dynamic height and normal height, and various countries may choose to operate with those definitions instead of orthometric. They may also adopt sl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean Sea Level
There are several kinds of mean in mathematics, especially in statistics. Each mean serves to summarize a given group of data, often to better understand the overall value ( magnitude and sign) of a given data set. For a data set, the '' arithmetic mean'', also known as "arithmetic average", is a measure of central tendency of a finite set of numbers: specifically, the sum of the values divided by the number of values. The arithmetic mean of a set of numbers ''x''1, ''x''2, ..., x''n'' is typically denoted using an overhead bar, \bar. If the data set were based on a series of observations obtained by sampling from a statistical population, the arithmetic mean is the '' sample mean'' (\bar) to distinguish it from the mean, or expected value, of the underlying distribution, the '' population mean'' (denoted \mu or \mu_x).Underhill, L.G.; Bradfield d. (1998) ''Introstat'', Juta and Company Ltd.p. 181/ref> Outside probability and statistics, a wide range of other notions of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
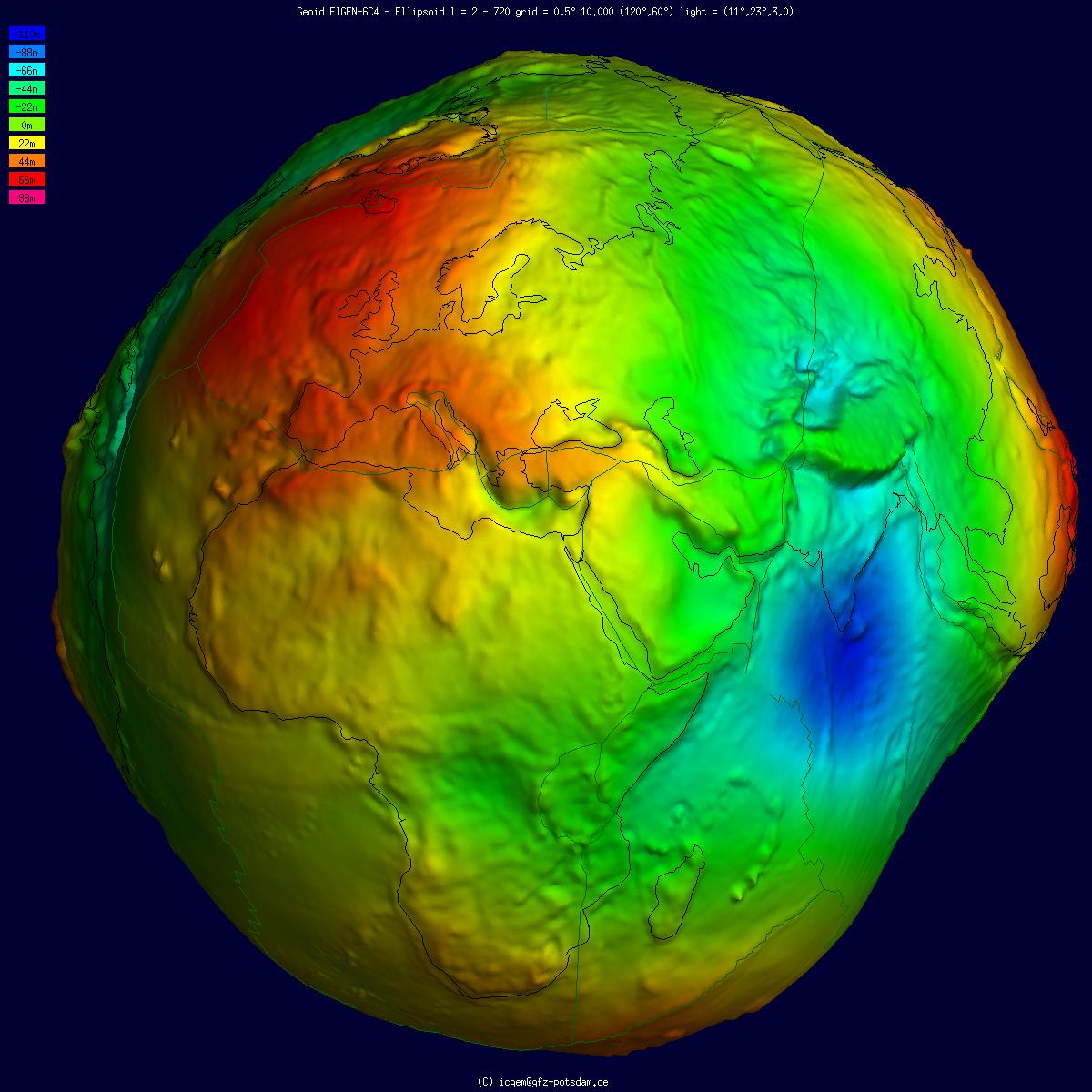
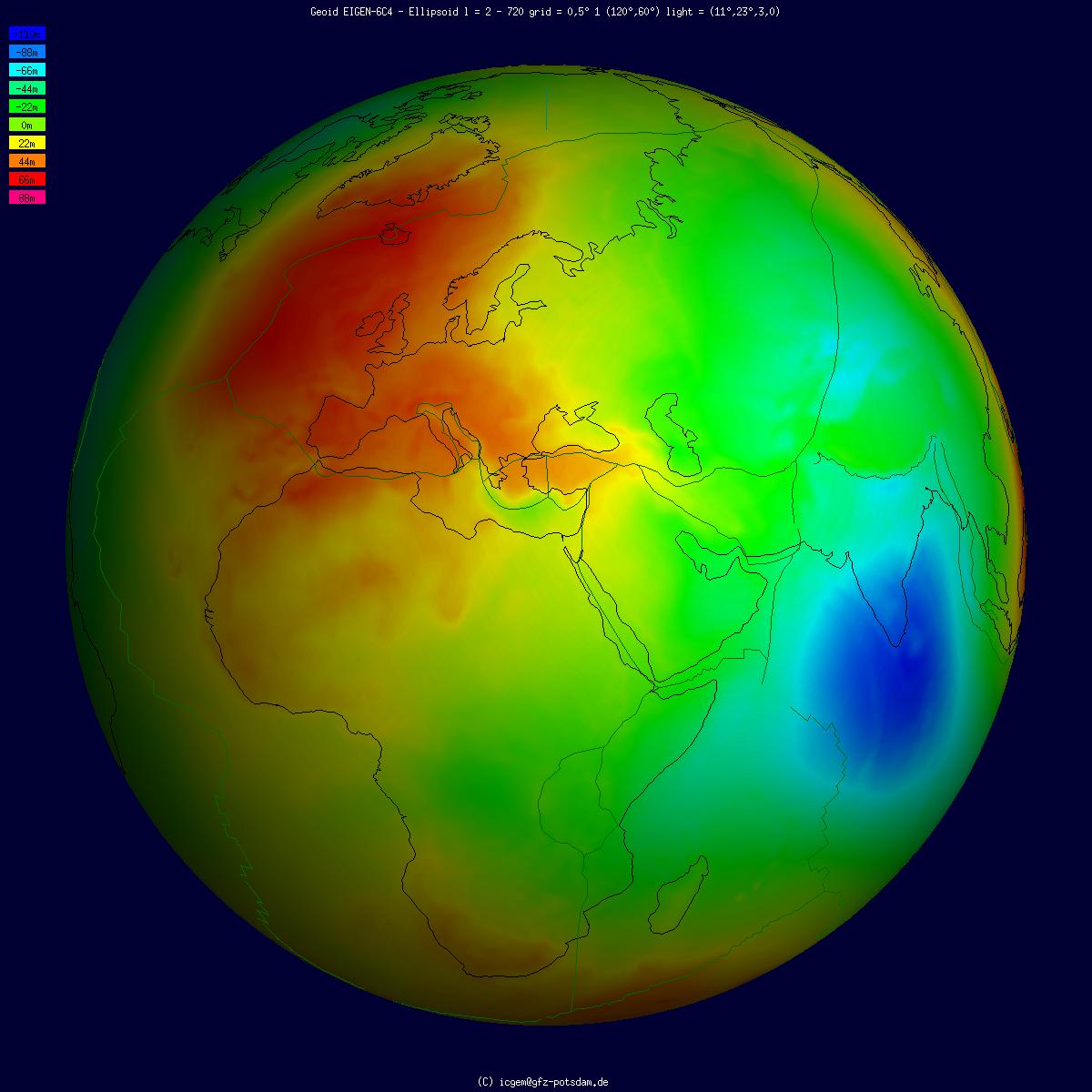
Geoid
The geoid () is the shape that the ocean surface would take under the influence of the gravity of Earth, including gravitational attraction and Earth's rotation, if other influences such as winds and tides were absent. This surface is extended through the continents (such as with very narrow hypothetical canals). According to Gauss, who first described it, it is the "mathematical figure of the Earth", a smooth but irregular surface whose shape results from the uneven distribution of mass within and on the surface of Earth. It can be known only through extensive gravitational measurements and calculations. Despite being an important concept for almost 200 years in the history of geodesy and geophysics, it has been defined to high precision only since advances in satellite geodesy in the late 20th century. All points on a geoid surface have the same geopotential (the sum of gravitational potential energy and centrifugal potential energy). The force of gravity acts everywher ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equipotential Surface
In mathematics and physics, an equipotential or isopotential refers to a region in space where every point is at the same potential. This usually refers to a scalar potential (in that case it is a level set of the potential), although it can also be applied to vector potentials. An equipotential of a scalar potential function in -dimensional space is typically an ()-dimensional space. The del operator illustrates the relationship between a vector field and its associated scalar potential field. An equipotential region might be referred as being 'of equipotential' or simply be called 'an equipotential'. An equipotential region of a scalar potential in three-dimensional space is often an equipotential surface (or ''potential isosurface''), but it can also be a three-dimensional mathematical solid in space. The gradient of the scalar potential (and hence also its opposite, as in the case of a vector field with an associated potential field) is everywhere perpendicular to the equ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geoid Undulation
The geoid () is the shape that the ocean surface would take under the influence of the gravity of Earth, including gravitational attraction and Earth's rotation, if other influences such as winds and tides were absent. This surface is extended through the continents (such as with very narrow hypothetical canals). According to Gauss, who first described it, it is the "mathematical figure of the Earth", a smooth but irregular surface whose shape results from the uneven distribution of mass within and on the surface of Earth. It can be known only through extensive gravitational measurements and calculations. Despite being an important concept for almost 200 years in the history of geodesy and geophysics, it has been defined to high precision only since advances in satellite geodesy in the late 20th century. All points on a geoid surface have the same geopotential (the sum of gravitational potential energy and centrifugal potential energy). The force of gravity acts everywhere ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |