|
Non-parametric Statistic
Nonparametric statistics is the branch of statistics that is not based solely on parametrized families of probability distributions (common examples of parameters are the mean and variance). Nonparametric statistics is based on either being distribution-free or having a specified distribution but with the distribution's parameters unspecified. Nonparametric statistics includes both descriptive statistics and statistical inference. Nonparametric tests are often used when the assumptions of parametric tests are violated. Definitions The term "nonparametric statistics" has been imprecisely defined in the following two ways, among others: Applications and purpose Non-parametric methods are widely used for studying populations that take on a ranked order (such as movie reviews receiving one to four stars). The use of non-parametric methods may be necessary when data have a ranking but no clear numerical interpretation, such as when assessing preferences. In terms of levels of me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Preferences
In psychology, economics and philosophy, preference is a technical term usually used in relation to choosing between wikt:alternative, alternatives. For example, someone prefers A over B if they would rather choose A than B. Preferences are central to decision theory because of this relation to behavior. Some methods such as Ordinal Priority Approach use preference relation for decision-making. As connative states, they are closely related to desires. The difference between the two is that desires are directed at one object while preferences concern a comparison between two alternatives, of which one is preferred to the other. In insolvency, the term is used to determine which outstanding obligation the insolvent party has to settle first. Psychology In psychology, preferences refer to an individual's attitude towards a set of objects, typically reflected in an explicit decision-making process (Lichtenstein & Slovic, 2006). The term is also used to mean evaluative judgment in the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multivariate Analysis
Multivariate statistics is a subdivision of statistics encompassing the simultaneous observation and analysis of more than one outcome variable. Multivariate statistics concerns understanding the different aims and background of each of the different forms of multivariate analysis, and how they relate to each other. The practical application of multivariate statistics to a particular problem may involve several types of univariate and multivariate analyses in order to understand the relationships between variables and their relevance to the problem being studied. In addition, multivariate statistics is concerned with multivariate probability distributions, in terms of both :*how these can be used to represent the distributions of observed data; :*how they can be used as part of statistical inference, particularly where several different quantities are of interest to the same analysis. Certain types of problems involving multivariate data, for example simple linear regression an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Data Envelopment Analysis
Data envelopment analysis (DEA) is a nonparametric method in operations research and economics for the estimation of production frontiers.Charnes et al (1978) DEA has been applied in a large range of fields including international banking, economic sustainability, police department operations, and logistical applicationsCharnes et al (1995) Emrouznejad et al (2016)Thanassoulis (1995) Additionally, DEA has been used to assess the performance of natural language processing models, and it has found other applications within machine learning.Zhou et al (2022)Guerrero et al (2022) Description DEA is used to empirically measure productive efficiency of decision-making units (DMUs). Although DEA has a strong link to production theory in economics, the method is also used for benchmarking in operations management, whereby a set of measures is selected to benchmark the performance of manufacturing and service operations. In benchmarking, the efficient DMUs, as defined by DEA, may not nece ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wavelet
A wavelet is a wave-like oscillation with an amplitude that begins at zero, increases or decreases, and then returns to zero one or more times. Wavelets are termed a "brief oscillation". A taxonomy of wavelets has been established, based on the number and direction of its pulses. Wavelets are imbued with specific properties that make them useful for signal processing. For example, a wavelet could be created to have a frequency of Middle C and a short duration of roughly one tenth of a second. If this wavelet were to be convolved with a signal created from the recording of a melody, then the resulting signal would be useful for determining when the Middle C note appeared in the song. Mathematically, a wavelet correlates with a signal if a portion of the signal is similar. Correlation is at the core of many practical wavelet applications. As a mathematical tool, wavelets can be used to extract information from many different kinds of data, including but not limited to au ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spline (mathematics)
In mathematics, a spline is a special function defined piecewise by polynomials. In interpolating problems, spline interpolation is often preferred to polynomial interpolation because it yields similar results, even when using low degree polynomials, while avoiding Runge's phenomenon for higher degrees. In the computer science subfields of computer-aided design and computer graphics, the term ''spline'' more frequently refers to a piecewise polynomial ( parametric) curve. Splines are popular curves in these subfields because of the simplicity of their construction, their ease and accuracy of evaluation, and their capacity to approximate complex shapes through curve fitting and interactive curve design. The term spline comes from the flexible spline devices used by shipbuilders and draftsmen to draw smooth shapes. Introduction The term "spline" is used to refer to a wide class of functions that are used in applications requiring data interpolation and/or smoothing. The dat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kernel (statistics)
The term kernel is used in statistical analysis to refer to a window function. The term "kernel" has several distinct meanings in different branches of statistics. Bayesian statistics In statistics, especially in Bayesian statistics, the kernel of a probability density function (pdf) or probability mass function (pmf) is the form of the pdf or pmf in which any factors that are not functions of any of the variables in the domain are omitted. Note that such factors may well be functions of the parameters of the pdf or pmf. These factors form part of the normalization factor of the probability distribution, and are unnecessary in many situations. For example, in pseudo-random number sampling, most sampling algorithms ignore the normalization factor. In addition, in Bayesian analysis of conjugate prior distributions, the normalization factors are generally ignored during the calculations, and only the kernel considered. At the end, the form of the kernel is examined, and if i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semiparametric Regression
In statistics, semiparametric regression includes regression models that combine parametric and nonparametric models. They are often used in situations where the fully nonparametric model may not perform well or when the researcher wants to use a parametric model but the functional form with respect to a subset of the regressors or the density of the errors is not known. Semiparametric regression models are a particular type of semiparametric modelling and, since semiparametric models contain a parametric component, they rely on parametric assumptions and may be misspecified and inconsistent, just like a fully parametric model. Methods Many different semiparametric regression methods have been proposed and developed. The most popular methods are the partially linear, index and varying coefficient models. Partially linear models A partially linear model is given by : Y_i = X'_i \beta + g\left(Z_i \right) + u_i, \, \quad i = 1,\ldots,n, \, where Y_ is the dependent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonparametric Regression
Nonparametric regression is a category of regression analysis in which the predictor does not take a predetermined form but is constructed according to information derived from the data. That is, no parametric form is assumed for the relationship between predictors and dependent variable. Nonparametric regression requires larger sample sizes than regression based on parametric models because the data must supply the model structure as well as the model estimates. Definition In nonparametric regression, we have random variables X and Y and assume the following relationship: : \mathbb \mid X=x= m(x), where m(x) is some deterministic function. Linear regression is a restricted case of nonparametric regression where m(x) is assumed to be affine. Some authors use a slightly stronger assumption of additive noise: : Y = m(X) + U, where the random variable U is the `noise term', with mean 0. Without the assumption that m belongs to a specific parametric family of functions it is impos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kernel Density Estimation
In statistics, kernel density estimation (KDE) is the application of kernel smoothing for probability density estimation, i.e., a non-parametric method to estimate the probability density function of a random variable based on '' kernels'' as weights. KDE answers a fundamental data smoothing problem where inferences about the population are made, based on a finite data sample. In some fields such as signal processing and econometrics it is also termed the Parzen–Rosenblatt window method, after Emanuel Parzen and Murray Rosenblatt, who are usually credited with independently creating it in its current form. One of the famous applications of kernel density estimation is in estimating the class-conditional marginal densities of data when using a naive Bayes classifier, which can improve its prediction accuracy. Definition Let (''x''1, ''x''2, ..., ''xn'') be independent and identically distributed samples drawn from some univariate distribution with an unknown density ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Histogram
A histogram is an approximate representation of the distribution of numerical data. The term was first introduced by Karl Pearson. To construct a histogram, the first step is to " bin" (or " bucket") the range of values—that is, divide the entire range of values into a series of intervals—and then count how many values fall into each interval. The bins are usually specified as consecutive, non-overlapping intervals of a variable. The bins (intervals) must be adjacent and are often (but not required to be) of equal size. If the bins are of equal size, a bar is drawn over the bin with height proportional to the frequency—the number of cases in each bin. A histogram may also be normalized to display "relative" frequencies showing the proportion of cases that fall into each of several categories, with the sum of the heights equaling 1. However, bins need not be of equal width; in that case, the erected rectangle is defined to have its ''area'' proportional to the frequenc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
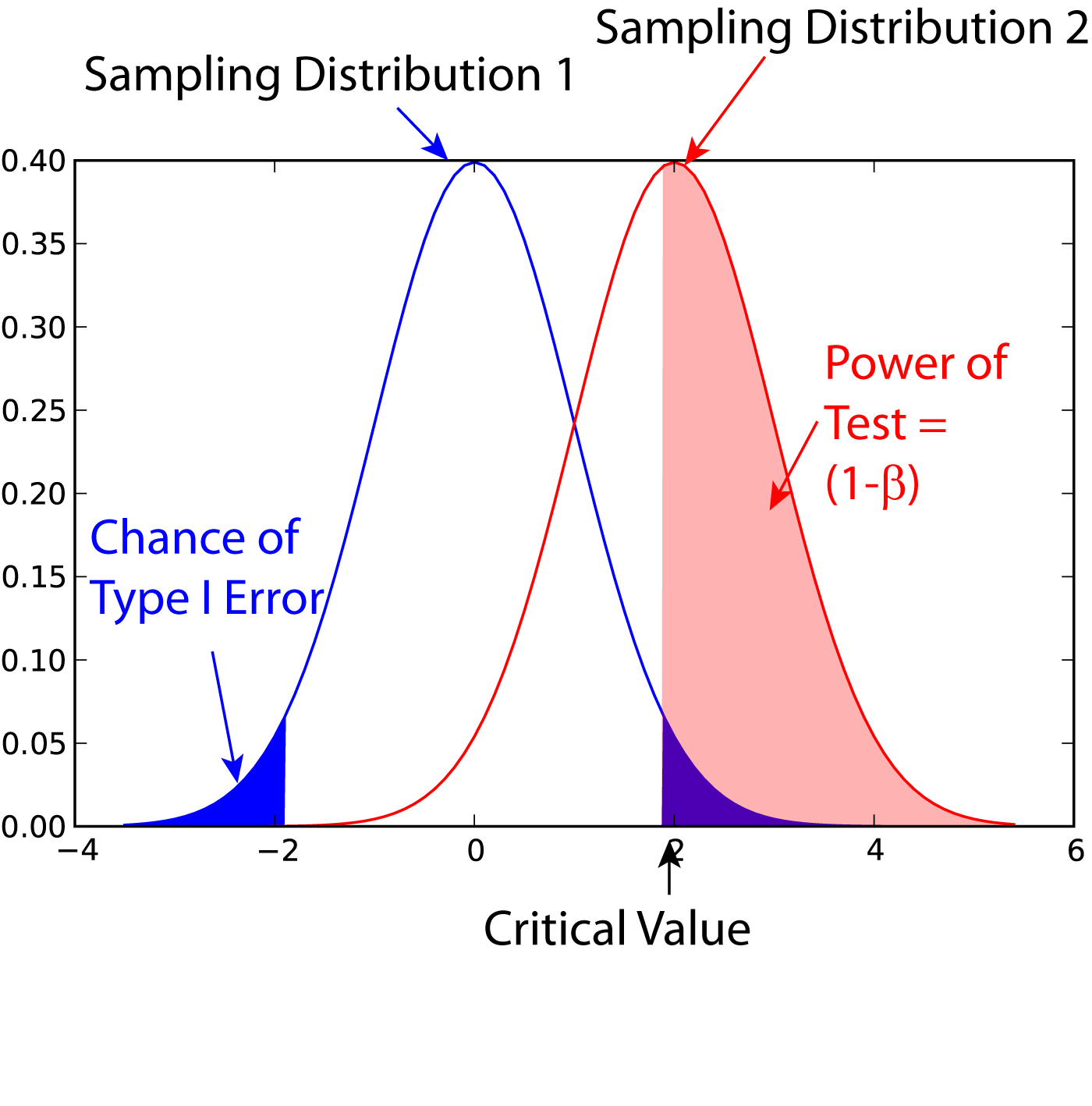
Statistical Power
In statistics, the power of a binary hypothesis test is the probability that the test correctly rejects the null hypothesis (H_0) when a specific alternative hypothesis (H_1) is true. It is commonly denoted by 1-\beta, and represents the chances of a true positive detection conditional on the actual existence of an effect to detect. Statistical power ranges from 0 to 1, and as the power of a test increases, the probability \beta of making a type II error by wrongly failing to reject the null hypothesis decreases. Notation This article uses the following notation: * ''β'' = probability of a Type II error, known as a "false negative" * 1 − ''β'' = probability of a "true positive", i.e., correctly rejecting the null hypothesis. "1 − ''β''" is also known as the power of the test. * ''α'' = probability of a Type I error, known as a "false positive" * 1 − ''α'' = probability of a "true negative", i.e., correctly not rejecting the null hypothesis Description For a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |