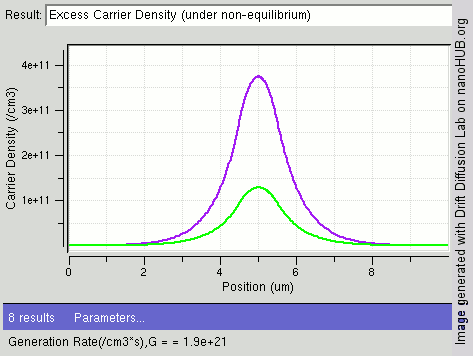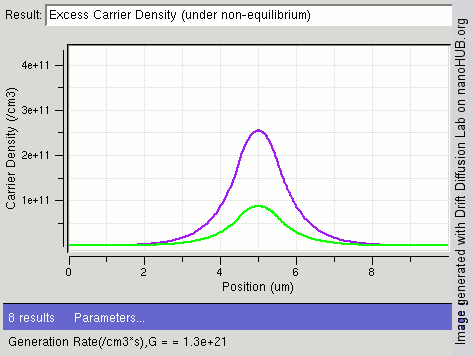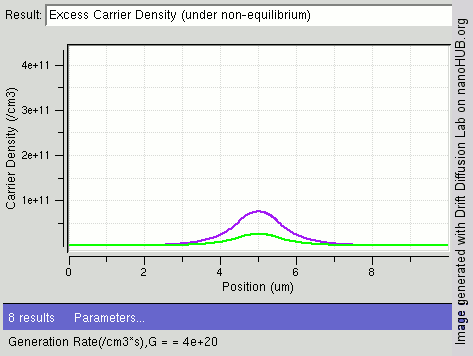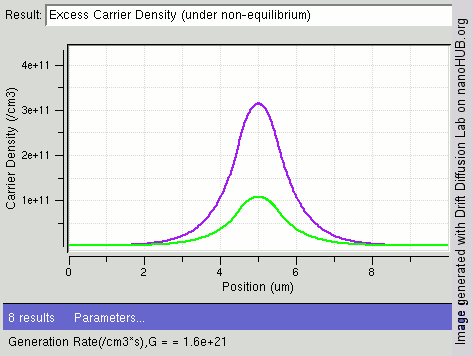
|
Multigrid
In numerical analysis, a multigrid method (MG method) is an algorithm for solving differential equations using a hierarchy of discretizations. They are an example of a class of techniques called multiresolution methods, very useful in problems exhibiting multiple scales of behavior. For example, many basic relaxation methods exhibit different rates of convergence for short- and long-wavelength components, suggesting these different scales be treated differently, as in a Fourier analysis approach to multigrid. MG methods can be used as solvers as well as preconditioners. The main idea of multigrid is to accelerate the convergence of a basic iterative method (known as relaxation, which generally reduces short-wavelength error) by a ''global'' correction of the fine grid solution approximation from time to time, accomplished by solving a coarse problem. The coarse problem, while cheaper to solve, is similar to the fine grid problem in that it also has short- and long-wavelength errors ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multigrid Visualization
In numerical analysis, a multigrid method (MG method) is an algorithm for solving differential equations using a hierarchy of discretizations. They are an example of a class of techniques called multiresolution methods, very useful in problems exhibiting multiple scales of behavior. For example, many basic relaxation methods exhibit different rates of convergence for short- and long-wavelength components, suggesting these different scales be treated differently, as in a Fourier analysis approach to multigrid. MG methods can be used as solvers as well as preconditioners. The main idea of multigrid is to accelerate the convergence of a basic iterative method (known as relaxation, which generally reduces short-wavelength error) by a ''global'' correction of the fine grid solution approximation from time to time, accomplished by solving a coarse problem. The coarse problem, while cheaper to solve, is similar to the fine grid problem in that it also has short- and long-wavelength errors ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coarse Problem
: ''This article deals with a component of numerical methods. For coarse space in topology, see coarse structure.'' In numerical analysis, coarse problem is an auxiliary system of equations used in an iterative method for the solution of a given larger system of equations. A coarse problem is basically a version of the same problem at a lower resolution, retaining its essential characteristics, but with fewer variables. The purpose of the coarse problem is to propagate information throughout the whole problem globally. In multigrid methods for partial differential equations, the coarse problem is typically obtained as a discretization of the same equation on a coarser grid (usually, in finite difference methods) or by a Galerkin approximation on a subspace, called a coarse space. In finite element methods, the Galerkin approximation is typically used, with the coarse space generated by larger elements on the same domain. Typically, the coarse problem corresponds to a grid that is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Preconditioner
In mathematics, preconditioning is the application of a transformation, called the preconditioner, that conditions a given problem into a form that is more suitable for numerical solving methods. Preconditioning is typically related to reducing a condition number of the problem. The preconditioned problem is then usually solved by an iterative method. Preconditioning for linear systems In linear algebra and numerical analysis, a preconditioner P of a matrix A is a matrix such that P^A has a smaller condition number than A. It is also common to call T=P^ the preconditioner, rather than P, since P itself is rarely explicitly available. In modern preconditioning, the application of T=P^, i.e., multiplication of a column vector, or a block of column vectors, by T=P^, is commonly performed in a matrix-free fashion, i.e., where neither P, nor T=P^ (and often not even A) are explicitly available in a matrix form. Preconditioners are useful in iterative methods to solve a line ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Poisson Equation
In mathematics, the discrete Poisson equation is the finite difference analog of the Poisson equation. In it, the discrete Laplace operator takes the place of the Laplace operator. The discrete Poisson equation is frequently used in numerical analysis as a stand-in for the continuous Poisson equation, although it is also studied in its own right as a topic in discrete mathematics. On a two-dimensional rectangular grid Using the finite difference numerical method to discretize the 2-dimensional Poisson equation (assuming a uniform spatial discretization, \Delta x=\Delta y) on an grid gives the following formula: ( ^2 u )_ = \frac (u_ + u_ + u_ + u_ - 4 u_) = g_ where 2 \le i \le m-1 and 2 \le j \le n-1 . The preferred arrangement of the solution vector is to use natural ordering which, prior to removing boundary elements, would look like: \mathbf = \begin u_ , u_ , \ldots , u_ , u_ , u_ , \ldots , u_ , \ldots , u_ \end^\mathsf This will result in an linear system: A\mathbf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Preconditioner
In mathematics, preconditioning is the application of a transformation, called the preconditioner, that conditions a given problem into a form that is more suitable for numerical solving methods. Preconditioning is typically related to reducing a condition number of the problem. The preconditioned problem is then usually solved by an iterative method. Preconditioning for linear systems In linear algebra and numerical analysis, a preconditioner P of a matrix A is a matrix such that P^A has a smaller condition number than A. It is also common to call T=P^ the preconditioner, rather than P, since P itself is rarely explicitly available. In modern preconditioning, the application of T=P^, i.e., multiplication of a column vector, or a block of column vectors, by T=P^, is commonly performed in a matrix-free fashion, i.e., where neither P, nor T=P^ (and often not even A) are explicitly available in a matrix form. Preconditioners are useful in iterative methods to solve a line ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Analysis
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic computation, symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of numerical methods that attempt at finding approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics (predicting the motions of planets, stars and galaxies), numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulating living ce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Condition Number
In numerical analysis, the condition number of a function measures how much the output value of the function can change for a small change in the input argument. This is used to measure how sensitive a function is to changes or errors in the input, and how much error in the output results from an error in the input. Very frequently, one is solving the inverse problem: given f(x) = y, one is solving for ''x,'' and thus the condition number of the (local) inverse must be used. In linear regression the condition number of the moment matrix can be used as a diagnostic for multicollinearity. The condition number is an application of the derivative, and is formally defined as the value of the asymptotic worst-case relative change in output for a relative change in input. The "function" is the solution of a problem and the "arguments" are the data in the problem. The condition number is frequently applied to questions in linear algebra, in which case the derivative is straightforward but ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Krylov Subspace
In linear algebra, the order-''r'' Krylov subspace generated by an ''n''-by-''n'' matrix ''A'' and a vector ''b'' of dimension ''n'' is the linear subspace spanned by the images of ''b'' under the first ''r'' powers of ''A'' (starting from A^0=I), that is, :\mathcal_r(A,b) = \operatorname \, \. Background The concept is named after Russian applied mathematician and naval engineer Alexei Krylov, who published a paper about it in 1931. Properties * \mathcal_r(A,b),A\mathcal_r(A,b)\subset \mathcal_(A,b). * Vectors \ are linearly independent until r, where p(A) is the minimal polynomial of A. Furthermore, there exists a b such that r_0 = \deg (A)/math>. * \mathcal_r(A,b) is a cyclic submodule generated by b of the torsion k /math>-module (k^n)^A, where k^n is the linear space on k. * k^n can be decomposed as the direct sum of Krylov subspaces. Use Krylov subspaces are used in algorithms for finding approximate solutions to high-dimensional linear algebra problems. Many linear dyn ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Péclet Number
In continuum mechanics, the Péclet number (, after Jean Claude Eugène Péclet) is a class of dimensionless numbers relevant in the study of transport phenomena in a continuum. It is defined to be the ratio of the rate of advection of a physical quantity by the flow to the rate of diffusion of the same quantity driven by an appropriate gradient. In the context of species or mass transfer, the Péclet number is the product of the Reynolds number and the Schmidt number (). In the context of the thermal fluids, the thermal Péclet number is equivalent to the product of the Reynolds number and the Prandtl number (). The Péclet number is defined as: : \mathrm = \dfrac For mass transfer, it is defined as: :\mathrm_L = \frac = \mathrm_L \, \mathrm Such ratio can also be re-written in terms of times, as a ratio between the characteristic temporal intervals of the system: :\mathrm_L = \frac = \frac = \frac For \mathrm \gg 1 the diffusion happens in a much longer time compared to th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convection–diffusion Equation
The convection–diffusion equation is a combination of the diffusion equation, diffusion and convection (advection equation, advection) equations, and describes physical phenomena where particles, energy, or other physical quantities are transferred inside a physical system due to two processes: diffusion and convection. Depending on context, the same equation can be called the advection–diffusion equation, drift velocity, drift–diffusion equation, or (generic) scalar transport equation. Equation General The general equation is \frac = \mathbf \cdot (D \mathbf c) - \mathbf \cdot (\mathbf c) + R where * is the variable of interest (species concentration for mass transfer, temperature for heat transfer), * is the diffusivity (also called diffusion coefficient), such as mass diffusivity for particle motion or thermal diffusivity for heat transport, * is the velocity field that the quantity is moving with. It is a function of time and space. For example, in advection, might be t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Overhead (computing)
In computer science, overhead is any combination of excess or indirect computation time, memory, bandwidth, or other resources that are required to perform a specific task. It is a special case of engineering overhead. Overhead can be a deciding factor in software design, with regard to structure, error correction, and feature inclusion. Examples of computing overhead may be found in Object Oriented Programming (OOP), functional programming, data transfer, and data structures. Software design Choice of implementation A programmer/software engineer may have a choice of several algorithms, encodings, data types or data structures, each of which have known characteristics. When choosing among them, their respective overhead should also be considered. Tradeoffs In software engineering, overhead can influence the decision whether or not to include features in new products, or indeed whether to fix bugs. A feature that has a high overhead may not be included – or needs a big ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interpolation
In the mathematical field of numerical analysis, interpolation is a type of estimation, a method of constructing (finding) new data points based on the range of a discrete set of known data points. In engineering and science, one often has a number of data points, obtained by sampling or experimentation, which represent the values of a function for a limited number of values of the independent variable. It is often required to interpolate; that is, estimate the value of that function for an intermediate value of the independent variable. A closely related problem is the approximation of a complicated function by a simple function. Suppose the formula for some given function is known, but too complicated to evaluate efficiently. A few data points from the original function can be interpolated to produce a simpler function which is still fairly close to the original. The resulting gain in simplicity may outweigh the loss from interpolation error and give better performance in ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |