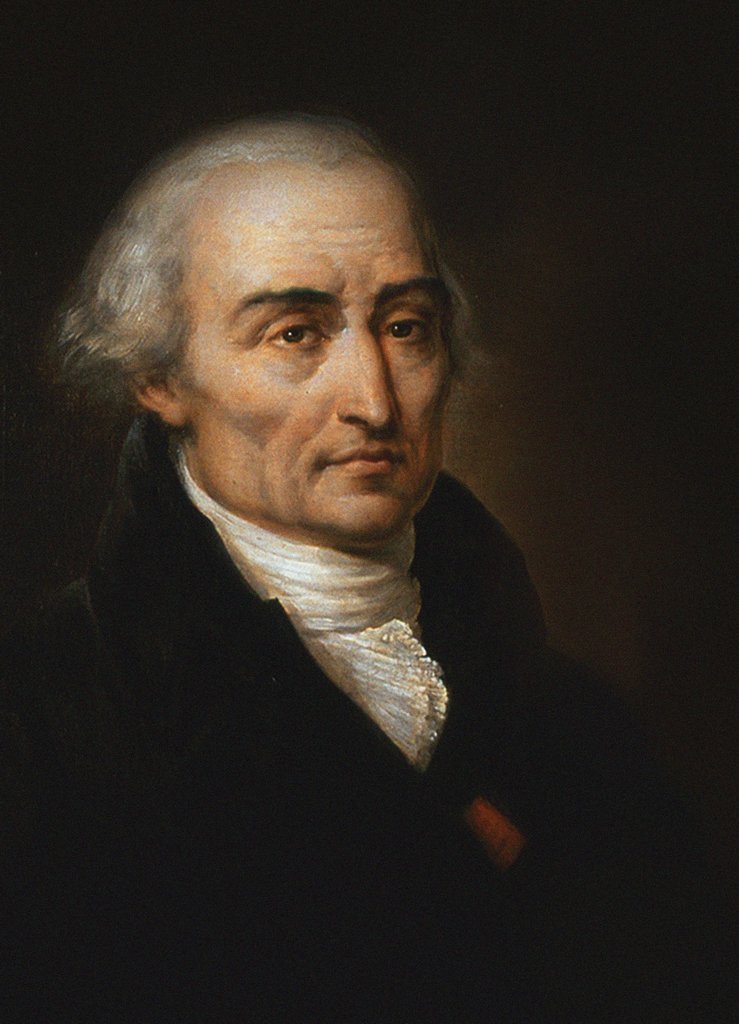|
Minimal Surface
In mathematics, a minimal surface is a surface that locally minimizes its area. This is equivalent to having zero mean curvature (see definitions below). The term "minimal surface" is used because these surfaces originally arose as surfaces that minimized total surface area subject to some constraint. Physical models of area-minimizing minimal surfaces can be made by dipping a wire frame into a soap solution, forming a soap film, which is a minimal surface whose boundary is the wire frame. However, the term is used for more general surfaces that may self-intersect or do not have constraints. For a given constraint there may also exist several minimal surfaces with different areas (for example, see minimal surface of revolution): the standard definitions only relate to a local optimum, not a global optimum. Definitions Minimal surfaces can be defined in several equivalent ways in R3. The fact that they are equivalent serves to demonstrate how minimal surface theory lies at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minimal Rational Surface
In algebraic geometry, a branch of mathematics, a rational surface is a surface birationally equivalent to the projective plane, or in other words a rational variety of dimension two. Rational surfaces are the simplest of the 10 or so classes of surface in the Enriques–Kodaira classification of complex surfaces, and were the first surfaces to be investigated. Structure Every non-singular rational surface can be obtained by repeatedly blowing up a minimal rational surface. The minimal rational surfaces are the projective plane and the Hirzebruch surfaces Σ''r'' for ''r'' = 0 or ''r'' ≥ 2. Invariants: The plurigenera are all 0 and the fundamental group is trivial. Hodge diamond: where ''n'' is 0 for the projective plane, and 1 for Hirzebruch surfaces and greater than 1 for other rational surfaces. The Picard group is the odd unimodular lattice I1,''n'', except for the Hirzebruch surfaces Σ2''m'' when it is the even unimodular lattice II1,1. Castelnuovo's theorem Gui ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neighbourhood (topology)
In topology and related areas of mathematics, a neighbourhood (or neighborhood) is one of the basic concepts in a topological space. It is closely related to the concepts of open set and interior. Intuitively speaking, a neighbourhood of a point is a set of points containing that point where one can move some amount in any direction away from that point without leaving the set. Definitions Neighbourhood of a point If X is a topological space and p is a point in X, then a of p is a subset V of X that includes an open set U containing p, p \in U \subseteq V \subseteq X. This is also equivalent to the point p \in X belonging to the topological interior of V in X. The neighbourhood V need be an open subset X, but when V is open in X then it is called an . Some authors have been known to require neighbourhoods to be open, so it is important to note conventions. A set that is a neighbourhood of each of its points is open since it can be expressed as the union of open sets ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conformal Map
In mathematics, a conformal map is a function that locally preserves angles, but not necessarily lengths. More formally, let U and V be open subsets of \mathbb^n. A function f:U\to V is called conformal (or angle-preserving) at a point u_0\in U if it preserves angles between directed curves through u_0, as well as preserving orientation. Conformal maps preserve both angles and the shapes of infinitesimally small figures, but not necessarily their size or curvature. The conformal property may be described in terms of the Jacobian derivative matrix of a coordinate transformation. The transformation is conformal whenever the Jacobian at each point is a positive scalar times a rotation matrix (orthogonal with determinant one). Some authors define conformality to include orientation-reversing mappings whose Jacobians can be written as any scalar times any orthogonal matrix. For mappings in two dimensions, the (orientation-preserving) conformal mappings are precisely the locally ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jean Baptiste Meusnier
Jean Baptiste Marie Charles Meusnier de la Place (Tours, 19 June 1754 — le Pont de Cassel, near Mainz, 13 June 1793) was a French mathematician, engineer and Revolutionary general. He is best known for Meusnier's theorem on the curvature of surfaces, which he formulated while he was at the École Royale du Génie (Royal School of Engineering). He also discovered the helicoid. He worked with Lavoisier on the decomposition of water and the evolution of hydrogen. Dirigible balloon Meusnier is sometimes portrayed as the inventor of the dirigible, because of an uncompleted project he conceived in 1784, not long after the first balloon flights of the Montgolfiers, and presented to the French Academy of Sciences. This concerned an elliptical balloon (''ballonet'') 84 metres long, with a capacity of 1,700 cubic metres, powered by three propellers driven by 80 men. The basket, in the form of a boat, was suspended from the canopy on a system of three ropes. Jacques Charles a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lagrange
Joseph-Louis Lagrange (born Giuseppe Luigi LagrangiaJoseph-Louis Lagrange, comte de l’Empire ''Encyclopædia Britannica'' or Giuseppe Ludovico De la Grange Tournier; 25 January 1736 – 10 April 1813), also reported as Giuseppe Luigi Lagrange or Lagrangia, was an Italian and , later naturalized |
Soap Bubble
A soap bubble is an extremely thin film of soap or detergent and water enclosing air that forms a hollow sphere with an iridescent surface. Soap bubbles usually last for only a few seconds before bursting, either on their own or on contact with another object. They are often used for children's enjoyment, but they are also used in artistic performances. Assembling many bubbles results in foam. When light shines onto a bubble it appears to change colour. Unlike those seen in a rainbow, which arise from differential refraction, the colours seen in a soap bubble arise from light wave interference, reflecting off the front and back surfaces of the thin soap film. Depending on the thickness of the film, different colours interfere constructively and destructively. Mathematics Soap bubbles are physical examples of the complex mathematical problem of minimal surface. They will assume the shape of least surface area possible containing a given volume. A true minimal surface is m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Young–Laplace Equation
In physics, the Young–Laplace equation () is an algebraic equation that describes the capillary pressure difference sustained across the interface between two static fluids, such as water and air, due to the phenomenon of surface tension or wall tension, although use of the latter is only applicable if assuming that the wall is very thin. The Young–Laplace equation relates the pressure difference to the shape of the surface or wall and it is fundamentally important in the study of static capillary surfaces. It's a statement of normal stress balance for static fluids meeting at an interface, where the interface is treated as a surface (zero thickness): \begin \Delta p &= -\gamma \nabla \cdot \hat n \\ &= -2\gamma H_f \\ &= -\gamma \left(\frac + \frac\right) \end where \Delta p is the Laplace pressure, the pressure difference across the fluid interface (the exterior pressure minus the interior pressure), \gamma is the surface tension (or wall tension), \hat n is the unit no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean Curvature Flow
In the field of differential geometry in mathematics, mean curvature flow is an example of a geometric flow of hypersurfaces in a Riemannian manifold (for example, smooth surfaces in 3-dimensional Euclidean space). Intuitively, a family of surfaces evolves under mean curvature flow if the normal component of the velocity of which a point on the surface moves is given by the mean curvature of the surface. For example, a round sphere evolves under mean curvature flow by shrinking inward uniformly (since the mean curvature vector of a sphere points inward). Except in special cases, the mean curvature flow develops singularities. Under the constraint that volume enclosed is constant, this is called surface tension flow. It is a parabolic partial differential equation, and can be interpreted as "smoothing". Existence and uniqueness The following was shown by Michael Gage and Richard S. Hamilton as an application of Hamilton's general existence theorem for parabolic geometric ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Principal Curvatures
In differential geometry, the two principal curvatures at a given point of a surface are the maximum and minimum values of the curvature as expressed by the eigenvalues of the shape operator at that point. They measure how the surface bends by different amounts in different directions at that point. Discussion At each point ''p'' of a differentiable surface in 3-dimensional Euclidean space one may choose a unit ''normal vector''. A '' normal plane'' at ''p'' is one that contains the normal vector, and will therefore also contain a unique direction tangent to the surface and cut the surface in a plane curve, called normal section. This curve will in general have different curvatures for different normal planes at ''p''. The principal curvatures at ''p'', denoted ''k''1 and ''k''2, are the maximum and minimum values of this curvature. Here the curvature of a curve is by definition the reciprocal of the radius of the osculating circle. The curvature is taken to be positiv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Saddle Point
In mathematics, a saddle point or minimax point is a point on the surface of the graph of a function where the slopes (derivatives) in orthogonal directions are all zero (a critical point), but which is not a local extremum of the function. An example of a saddle point is when there is a critical point with a relative minimum along one axial direction (between peaks) and at a relative maximum along the crossing axis. However, a saddle point need not be in this form. For example, the function f(x,y) = x^2 + y^3 has a critical point at (0, 0) that is a saddle point since it is neither a relative maximum nor relative minimum, but it does not have a relative maximum or relative minimum in the y-direction. The name derives from the fact that the prototypical example in two dimensions is a surface that ''curves up'' in one direction, and ''curves down'' in a different direction, resembling a riding saddle or a mountain pass between two peaks forming a landform saddle. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minimal Surface Curvature Planes-en
Minimal may refer to: * Minimal (music genre), art music that employs limited or minimal musical materials * "Minimal" (song), 2006 song by Pet Shop Boys * Minimal (supermarket) or miniMAL, a former supermarket chain in Germany and Poland * Minimal (''Dungeons & Dragons''), a creature of magically reduced size in the game ''Dungeons & Dragons'' * Minimal (chocolate), a bean to bar chocolate store in Japan, featured in '' Kantaro: The Sweet Tooth Salaryman'' * Minimal (clothing), an Indonesia clothing-retail company that worked with fashion model Ayu Gani See also * *Minimalism (other) *Maximal (other) *Minimisation (other) Minimisation or minimization may refer to: * Minimisation (psychology), downplaying the significance of an event or emotion * Minimisation (clinical trials) * Minimisation (code) or Minification, removing unnecessary characters from source code ... * Minimal prime (other) {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geodesics
In geometry, a geodesic () is a curve representing in some sense the shortest path ( arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a connection. It is a generalization of the notion of a "straight line". The noun ''geodesic'' and the adjective ''geodetic'' come from ''geodesy'', the science of measuring the size and shape of Earth, though many of the underlying principles can be applied to any ellipsoidal geometry. In the original sense, a geodesic was the shortest route between two points on the Earth's surface. For a spherical Earth, it is a segment of a great circle (see also great-circle distance). The term has since been generalized to more abstract mathematical spaces; for example, in graph theory, one might consider a geodesic between two vertices/nodes of a graph. In a Riemannian manifold or submanifold, geodesics are characterised by the property of having vanishing g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
