Young–Laplace equation on:
[Wikipedia]
[Google]
[Amazon]
In
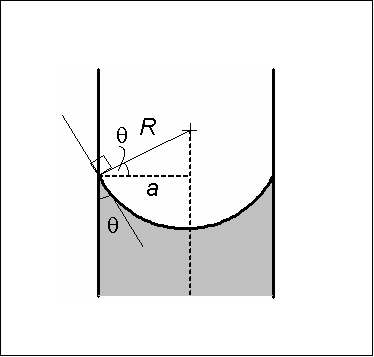 In a sufficiently narrow (i.e., low Bond number) tube of circular cross-section (radius ''a''), the interface between two fluids forms a meniscus that is a portion of the surface of a sphere with radius ''R''. The pressure jump across this surface is related to the radius and the surface tension γ by
This may be shown by writing the Young–Laplace equation in spherical form with a contact angle boundary condition and also a prescribed height boundary condition at, say, the bottom of the meniscus. The solution is a portion of a sphere, and the solution will exist ''only'' for the pressure difference shown above. This is significant because there isn't another equation or law to specify the pressure difference;
In a sufficiently narrow (i.e., low Bond number) tube of circular cross-section (radius ''a''), the interface between two fluids forms a meniscus that is a portion of the surface of a sphere with radius ''R''. The pressure jump across this surface is related to the radius and the surface tension γ by
This may be shown by writing the Young–Laplace equation in spherical form with a contact angle boundary condition and also a prescribed height boundary condition at, say, the bottom of the meniscus. The solution is a portion of a sphere, and the solution will exist ''only'' for the pressure difference shown above. This is significant because there isn't another equation or law to specify the pressure difference;  In order to maintain hydrostatic equilibrium, the induced capillary pressure is balanced by a change in height, ''h'', which can be positive or negative, depending on whether the wetting angle is less than or greater than 90°. For a fluid of
In order to maintain hydrostatic equilibrium, the induced capillary pressure is balanced by a change in height, ''h'', which can be positive or negative, depending on whether the wetting angle is less than or greater than 90°. For a fluid of
"An account of some experiments shown before the Royal Society; with an enquiry into the cause of some of the ascent and suspension of water in capillary tubes,"
''Philosophical Transactions of the Royal Society of London'', 30 : 739–747. * James Jurin (1719
"An account of some new experiments, relating to the action of glass tubes upon water and quicksilver,"
''Philosophical Transactions of the Royal Society of London'', 30 : 1083–1096. For a water-filled glass tube in
physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
, the Young–Laplace equation () is an equation that describes the capillary pressure difference sustained across the interface between two static fluids, such as water
Water is an inorganic compound with the chemical formula . It is a transparent, tasteless, odorless, and Color of water, nearly colorless chemical substance. It is the main constituent of Earth's hydrosphere and the fluids of all known liv ...
and air
An atmosphere () is a layer of gases that envelop an astronomical object, held in place by the gravity of the object. A planet retains an atmosphere when the gravity is great and the temperature of the atmosphere is low. A stellar atmosph ...
, due to the phenomenon of surface tension
Surface tension is the tendency of liquid surfaces at rest to shrink into the minimum surface area possible. Surface tension (physics), tension is what allows objects with a higher density than water such as razor blades and insects (e.g. Ge ...
or wall tension, although use of the latter is only applicable if assuming that the wall is very thin. The Young–Laplace equation relates the pressure difference to the shape of the surface or wall and it is fundamentally important in the study of static capillary surfaces. It is a statement of normal stress balance for static fluids meeting at an interface, where the interface is treated as a surface (zero thickness):
where is the Laplace pressure
The Laplace pressure is the pressure difference between the inside and the outside of a curved surface that forms the boundary between two fluid regions. The pressure difference is caused by the surface tension of the interface between liquid and ...
, the pressure difference across the fluid interface (the exterior pressure minus the interior pressure), is the surface tension
Surface tension is the tendency of liquid surfaces at rest to shrink into the minimum surface area possible. Surface tension (physics), tension is what allows objects with a higher density than water such as razor blades and insects (e.g. Ge ...
(or wall tension), is the unit normal pointing out of the surface, is the mean curvature, and and are the principal radii of curvature. Note that only normal stress is considered, because a static interface is possible only in the absence of tangential stress.
The equation is named after Thomas Young, who developed the qualitative theory of surface tension in 1805, and Pierre-Simon Laplace
Pierre-Simon, Marquis de Laplace (; ; 23 March 1749 – 5 March 1827) was a French polymath, a scholar whose work has been instrumental in the fields of physics, astronomy, mathematics, engineering, statistics, and philosophy. He summariz ...
who completed the mathematical description in the following year. It is sometimes also called the Young–Laplace–Gauss equation, as Carl Friedrich Gauss
Johann Carl Friedrich Gauss (; ; ; 30 April 177723 February 1855) was a German mathematician, astronomer, geodesist, and physicist, who contributed to many fields in mathematics and science. He was director of the Göttingen Observatory and ...
unified the work of Young and Laplace in 1830, deriving both the differential equation and boundary conditions using Johann Bernoulli
Johann Bernoulli (also known as Jean in French or John in English; – 1 January 1748) was a Swiss people, Swiss mathematician and was one of the many prominent mathematicians in the Bernoulli family. He is known for his contributions to infin ...
's virtual work principles.
Soap films
If the pressure difference is zero, as in a soap film without gravity, the interface will assume the shape of a minimal surface.Emulsions
The equation also explains the energy required to create anemulsion
An emulsion is a mixture of two or more liquids that are normally Miscibility, immiscible (unmixable or unblendable) owing to liquid-liquid phase separation. Emulsions are part of a more general class of two-phase systems of matter called colloi ...
. To form the small, highly curved droplets of an emulsion, extra energy is required to overcome the large pressure that results from their small radius.
The Laplace pressure, which is greater for smaller droplets, causes the diffusion of molecules out of the smallest droplets in an emulsion and drives emulsion coarsening via Ostwald ripening
Ostwald ripening is a phenomenon observed in solid solutions and liquid sols that involves the change of an inhomogeneous structure over time, in that small crystals or sol particles first dissolve and then redeposit onto larger crystals or s ...
.
Capillary pressure in a tube
existence
Existence is the state of having being or reality in contrast to nonexistence and nonbeing. Existence is often contrasted with essence: the essence of an entity is its essential features or qualities, which can be understood even if one does ...
of solution for one specific value of the pressure difference prescribes it.
The radius of the sphere will be a function only of the contact angle, θ, which in turn depends on the exact properties of the fluids and the container material with which the fluids in question are contacting/interfacing:
so that the pressure difference may be written as:
density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be u ...
ρ:
where ''g'' is the gravitational acceleration
In physics, gravitational acceleration is the acceleration of an object in free fall within a vacuum (and thus without experiencing drag (physics), drag). This is the steady gain in speed caused exclusively by gravitational attraction. All bodi ...
. This is sometimes known as the Jurin's law or Jurin height after James Jurin who studied the effect in 1718.See:
* James Jurin (1718"An account of some experiments shown before the Royal Society; with an enquiry into the cause of some of the ascent and suspension of water in capillary tubes,"
''Philosophical Transactions of the Royal Society of London'', 30 : 739–747. * James Jurin (1719
"An account of some new experiments, relating to the action of glass tubes upon water and quicksilver,"
''Philosophical Transactions of the Royal Society of London'', 30 : 1083–1096. For a water-filled glass tube in
air
An atmosphere () is a layer of gases that envelop an astronomical object, held in place by the gravity of the object. A planet retains an atmosphere when the gravity is great and the temperature of the atmosphere is low. A stellar atmosph ...
at sea level
Mean sea level (MSL, often shortened to sea level) is an mean, average surface level of one or more among Earth's coastal Body of water, bodies of water from which heights such as elevation may be measured. The global MSL is a type of vertical ...
:
*γ = 0.0728 J/m2 at 20 ° C
*''θ'' = 20° (0.35 rad)
*''ρ'' = 1000 kg/m3
*''g'' = 9.8 m/s2
and so the height of the water column is given by:
Thus for a 2 mm wide (1 mm radius) tube, the water would rise 14 mm. However, for a capillary tube with radius 0.1 mm, the water would rise 14 cm (about 6 inch
The inch (symbol: in or prime (symbol), ) is a Units of measurement, unit of length in the imperial units, British Imperial and the United States customary units, United States customary System of measurement, systems of measurement. It is eq ...
es).
Capillary action and gravity
When including also the effects ofgravity
In physics, gravity (), also known as gravitation or a gravitational interaction, is a fundamental interaction, a mutual attraction between all massive particles. On Earth, gravity takes a slightly different meaning: the observed force b ...
, for a free surface
In physics, a free surface is the surface of a fluid that is subject to zero parallel shear stress,
such as the interface between two homogeneous fluids.
An example of two such homogeneous fluids would be a body of water (liquid) and the air in ...
and for a pressure difference between the fluids equal to Δ''p'' at the level ''h=0'', there is a balance, when the interface is in equilibrium, between Δ''p'', the hydrostatic pressure
Hydrostatics is the branch of fluid mechanics that studies fluids at hydrostatic equilibrium and "the pressure in a fluid or exerted by a fluid on an immersed body". The word "hydrostatics" is sometimes used to refer specifically to water and o ...
and the effects of surface tension
Surface tension is the tendency of liquid surfaces at rest to shrink into the minimum surface area possible. Surface tension (physics), tension is what allows objects with a higher density than water such as razor blades and insects (e.g. Ge ...
. The Young–Laplace equation becomes: