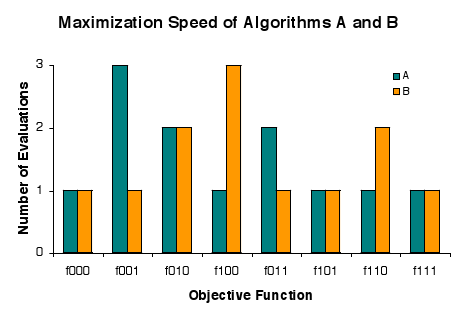
|
Memetic Algorithm
A memetic algorithm (MA) in computer science and operations research, is an extension of the traditional genetic algorithm. It may provide a sufficiently good solution to an optimization problem. It uses a local search technique to reduce the likelihood of premature convergence. Memetic algorithms represent one of the recent growing areas of research in evolutionary computation. The term MA is now widely used as a synergy of evolutionary or any population-based approach with separate individual learning or local improvement procedures for problem search. Quite often, MAs are also referred to in the literature as Baldwinian evolutionary algorithms (EAs), Lamarckian EAs, cultural algorithms, or genetic local search. Introduction Inspired by both Darwinian principles of natural evolution and Dawkins' notion of a meme, the term ''memetic algorithm'' (MA) was introduced by Pablo Moscato in his technical report in 1989 where he viewed MA as being close to a form of population-based hy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computer Science
Computer science is the study of computation, automation, and information. Computer science spans theoretical disciplines (such as algorithms, theory of computation, information theory, and automation) to Applied science, practical disciplines (including the design and implementation of Computer architecture, hardware and Computer programming, software). Computer science is generally considered an area of research, academic research and distinct from computer programming. Algorithms and data structures are central to computer science. The theory of computation concerns abstract models of computation and general classes of computational problem, problems that can be solved using them. The fields of cryptography and computer security involve studying the means for secure communication and for preventing Vulnerability (computing), security vulnerabilities. Computer graphics (computer science), Computer graphics and computational geometry address the generation of images. Progr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algorithm
In mathematics and computer science, an algorithm () is a finite sequence of rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algorithms are used as specifications for performing calculations and data processing. More advanced algorithms can perform automated deductions (referred to as automated reasoning) and use mathematical and logical tests to divert the code execution through various routes (referred to as automated decision-making). Using human characteristics as descriptors of machines in metaphorical ways was already practiced by Alan Turing with terms such as "memory", "search" and "stimulus". In contrast, a Heuristic (computer science), heuristic is an approach to problem solving that may not be fully specified or may not guarantee correct or optimal results, especially in problem domains where there is no well-defined correct or optimal result. As an effective method, an algorithm ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadratic Assignment Problem
The quadratic assignment problem (QAP) is one of the fundamental combinatorial optimization problems in the branch of optimization or operations research in mathematics, from the category of the facilities location problems first introduced by Koopmans and Beckmann. The problem models the following real-life problem: :There are a set of ''n'' facilities and a set of ''n'' locations. For each pair of locations, a ''distance'' is specified and for each pair of facilities a ''weight'' or ''flow'' is specified (e.g., the amount of supplies transported between the two facilities). The problem is to assign all facilities to different locations with the goal of minimizing the sum of the distances multiplied by the corresponding flows. Intuitively, the cost function encourages facilities with high flows between each other to be placed close together. The problem statement resembles that of the assignment problem, except that the cost function is expressed in terms of quadratic inequal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Travelling Salesman Problem
The travelling salesman problem (also called the travelling salesperson problem or TSP) asks the following question: "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?" It is an NP-hard problem in combinatorial optimization, important in theoretical computer science and operations research. The travelling purchaser problem and the vehicle routing problem are both generalizations of TSP. In the theory of computational complexity, the decision version of the TSP (where given a length ''L'', the task is to decide whether the graph has a tour of at most ''L'') belongs to the class of NP-complete problems. Thus, it is possible that the worst-case running time for any algorithm for the TSP increases superpolynomially (but no more than exponentially) with the number of cities. The problem was first formulated in 1930 and is one of the most intensively studied p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Knapsack Problem
The knapsack problem is a problem in combinatorial optimization: Given a set of items, each with a weight and a value, determine the number of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as possible. It derives its name from the problem faced by someone who is constrained by a fixed-size knapsack and must fill it with the most valuable items. The problem often arises in resource allocation where the decision-makers have to choose from a set of non-divisible projects or tasks under a fixed budget or time constraint, respectively. The knapsack problem has been studied for more than a century, with early works dating as far back as 1897. The name "knapsack problem" dates back to the early works of the mathematician Tobias Dantzig (1884–1956), and refers to the commonplace problem of packing the most valuable or useful items without overloading the luggage. Applications Knapsack problems ap ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Partition
In mathematics, a graph partition is the reduction of a graph to a smaller graph by partitioning its set of nodes into mutually exclusive groups. Edges of the original graph that cross between the groups will produce edges in the partitioned graph. If the number of resulting edges is small compared to the original graph, then the partitioned graph may be better suited for analysis and problem-solving than the original. Finding a partition that simplifies graph analysis is a hard problem, but one that has applications to scientific computing, VLSI circuit design, and task scheduling in multiprocessor computers, among others. Recently, the graph partition problem has gained importance due to its application for clustering and detection of cliques in social, pathological and biological networks. For a survey on recent trends in computational methods and applications see . Two common examples of graph partitioning are minimum cut and maximum cut problems. Problem complexity Typicall ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
NP (complexity)
In computational complexity theory, NP (nondeterministic polynomial time) is a complexity class used to classify decision problems. NP is the set of decision problems for which the problem instances, where the answer is "yes", have proofs verifiable in polynomial time by a deterministic Turing machine, or alternatively the set of problems that can be solved in polynomial time by a nondeterministic Turing machine.''Polynomial time'' refers to how quickly the number of operations needed by an algorithm, relative to the size of the problem, grows. It is therefore a measure of efficiency of an algorithm. An equivalent definition of NP is the set of decision problems ''solvable'' in polynomial time by a nondeterministic Turing machine. This definition is the basis for the abbreviation NP; " nondeterministic, polynomial time". These two definitions are equivalent because the algorithm based on the Turing machine consists of two phases, the first of which consists of a guess abou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conjugate Gradient Method
In mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is positive-definite. The conjugate gradient method is often implemented as an iterative algorithm, applicable to sparse systems that are too large to be handled by a direct implementation or other direct methods such as the Cholesky decomposition. Large sparse systems often arise when numerically solving partial differential equations or optimization problems. The conjugate gradient method can also be used to solve unconstrained optimization problems such as energy minimization. It is commonly attributed to Magnus Hestenes and Eduard Stiefel, who programmed it on the Z4, and extensively researched it. The biconjugate gradient method provides a generalization to non-symmetric matrices. Various nonlinear conjugate gradient methods seek minima of nonlinear optimization problems. Description of the problem addressed by co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interior Point Method
Interior-point methods (also referred to as barrier methods or IPMs) are a certain class of algorithms that solve linear and nonlinear convex optimization problems. An interior point method was discovered by Soviet mathematician I. I. Dikin in 1967 and reinvented in the U.S. in the mid-1980s. In 1984, Narendra Karmarkar developed a method for linear programming called Karmarkar's algorithm, which runs in provably polynomial time and is also very efficient in practice. It enabled solutions of linear programming problems that were beyond the capabilities of the simplex method. Contrary to the simplex method, it reaches a best solution by traversing the interior of the feasible region. The method can be generalized to convex programming based on a self-concordant barrier function used to encode the convex set. Any convex optimization problem can be transformed into minimizing (or maximizing) a linear function over a convex set by converting to the epigraph form. The idea of encodi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hill Climbing
numerical analysis, hill climbing is a mathematical optimization technique which belongs to the family of local search. It is an iterative algorithm that starts with an arbitrary solution to a problem, then attempts to find a better solution by making an incremental change to the solution. If the change produces a better solution, another incremental change is made to the new solution, and so on until no further improvements can be found. For example, hill climbing can be applied to the travelling salesman problem. It is easy to find an initial solution that visits all the cities but will likely be very poor compared to the optimal solution. The algorithm starts with such a solution and makes small improvements to it, such as switching the order in which two cities are visited. Eventually, a much shorter route is likely to be obtained. Hill climbing finds optimal solutions for convex problems – for other problems it will find only local optima (solutions that cannot be imp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Combinatorial Optimization
Combinatorial optimization is a subfield of mathematical optimization that consists of finding an optimal object from a finite set of objects, where the set of feasible solutions is discrete or can be reduced to a discrete set. Typical combinatorial optimization problems are the travelling salesman problem ("TSP"), the minimum spanning tree problem ("MST"), and the knapsack problem. In many such problems, such as the ones previously mentioned, exhaustive search is not tractable, and so specialized algorithms that quickly rule out large parts of the search space or approximation algorithms must be resorted to instead. Combinatorial optimization is related to operations research, algorithm theory, and computational complexity theory. It has important applications in several fields, including artificial intelligence, machine learning, auction theory, software engineering, VLSI, applied mathematics and theoretical computer science. Some research literature considers discrete o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chromosome
A chromosome is a long DNA molecule with part or all of the genetic material of an organism. In most chromosomes the very long thin DNA fibers are coated with packaging proteins; in eukaryotic cells the most important of these proteins are the histones. These proteins, aided by chaperone proteins, bind to and condense the DNA molecule to maintain its integrity. These chromosomes display a complex three-dimensional structure, which plays a significant role in transcriptional regulation. Chromosomes are normally visible under a light microscope only during the metaphase of cell division (where all chromosomes are aligned in the center of the cell in their condensed form). Before this happens, each chromosome is duplicated ( S phase), and both copies are joined by a centromere, resulting either in an X-shaped structure (pictured above), if the centromere is located equatorially, or a two-arm structure, if the centromere is located distally. The joined copies are now called si ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
