|
Method Of Conditional Probabilities
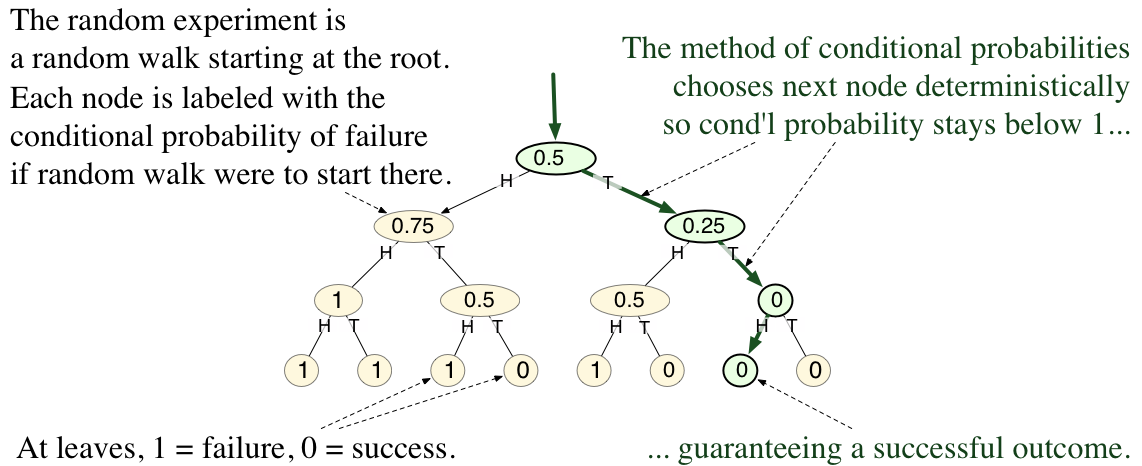
In mathematics and computer science, the method of conditional probabilities is a systematic method for converting non-constructive probabilistic existence proofs into efficient Deterministic algorithm, deterministic algorithms that explicitly construct the desired object. blog entry by Neal E. Young, accessed 19/04/2012 and 14/09/2023. Often, the probabilistic method is used to prove the existence of mathematical objects with some desired combinatorial properties. The proofs in that method work by showing that a random object, chosen from some probability distribution, has the desired properties with positive probability. Consequently, they are nonconstructive proof, nonconstructive — th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Randomized Rounding
In computer science and operations research, randomized rounding is a widely used approach for designing and analyzing approximation algorithms. Many combinatorial optimization problems are computationally intractability (complexity), intractable to solve exactly (to optimality). For such problems, randomized rounding can be used to design fast (polynomial time) approximation algorithms—that is, algorithms that are guaranteed to return an approximately optimal solution given any input. The basic idea of randomized rounding is to convert an optimal solution of a linear programming relaxation, relaxation of the problem into an approximately-optimal solution to the original problem. The resulting algorithm is usually analyzed using the probabilistic method. Overview The basic approach has three steps: # Formulate the problem to be solved as an integer linear program (ILP). # Compute an optimal fractional solution x to the linear programming relaxation (LP) of the ILP. # Rou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Max Cut
In a graph, a maximum cut is a cut whose size is at least the size of any other cut. That is, it is a partition of the graph's vertices into two complementary sets and , such that the number of edges between and is as large as possible. Finding such a cut is known as the max-cut problem. The problem can be stated simply as follows. One wants a subset of the vertex set such that the number of edges between and the complementary subset is as large as possible. Equivalently, one wants a bipartite subgraph of the graph with as many edges as possible. There is a more general version of the problem called weighted max-cut, where each edge is associated with a real number, its weight, and the objective is to maximize the total weight of the edges between and its complement rather than the number of the edges. The weighted max-cut problem allowing both positive and negative weights can be trivially transformed into a weighted minimum cut problem by flipping the sign in all ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Springer Verlag
Springer Science+Business Media, commonly known as Springer, is a German multinational publishing company of books, e-books and peer-reviewed journals in science, humanities, technical and medical (STM) publishing. Originally founded in 1842 in Berlin, it expanded internationally in the 1960s, and through mergers in the 1990s and a sale to venture capitalists it fused with Wolters Kluwer and eventually became part of Springer Nature in 2015. Springer has major offices in Berlin, Heidelberg, Dordrecht, and New York City. History Julius Springer founded Springer-Verlag in Berlin in 1842 and his son Ferdinand Springer grew it from a small firm of 4 employees into Germany's then second-largest academic publisher with 65 staff in 1872.Chronology ". Springer Science+Business Media. In 1964, Springer expanded its business internationally, op ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cambridge University Press
Cambridge University Press was the university press of the University of Cambridge. Granted a letters patent by King Henry VIII in 1534, it was the oldest university press in the world. Cambridge University Press merged with Cambridge Assessment to form Cambridge University Press and Assessment under Queen Elizabeth II's approval in August 2021. With a global sales presence, publishing hubs, and offices in more than 40 countries, it published over 50,000 titles by authors from over 100 countries. Its publications include more than 420 academic journals, monographs, reference works, school and university textbooks, and English language teaching and learning publications. It also published Bibles, runs a bookshop in Cambridge, sells through Amazon, and has a conference venues business in Cambridge at the Pitt Building and the Sir Geoffrey Cass Sports and Social Centre. It also served as the King's Printer. Cambridge University Press, as part of the University of Cambridge, was a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derandomization
A randomized algorithm is an algorithm that employs a degree of randomness as part of its logic or procedure. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random determined by the random bits; thus either the running time, or the output (or both) are random variables. There is a distinction between algorithms that use the random input so that they always terminate with the correct answer, but where the expected running time is finite (Las Vegas algorithms, for example Quicksort), and algorithms which have a chance of producing an incorrect result (Monte Carlo algorithms, for example the Monte Carlo algorithm for the MFAS problem) or fail to produce a result either by signaling a failure or failing to terminate. In some cases, probabilistic algorithms are the only practical means of solving a problem. In common practice, randomized algor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probabilistic Method
In mathematics, the probabilistic method is a nonconstructive method, primarily used in combinatorics and pioneered by Paul Erdős, for proving the existence of a prescribed kind of mathematical object. It works by showing that if one randomly chooses objects from a specified class, the probability that the result is of the prescribed kind is strictly greater than zero. Although the proof uses probability, the final conclusion is determined for ''certain'', without any possible error. This method has now been applied to other areas of mathematics such as number theory, linear algebra, and real analysis, as well as in computer science (e.g. randomized rounding), and information theory. Introduction If every object in a collection of objects fails to have a certain property, then the probability that a random object chosen from the collection has that property is zero. Thus, by contraposition, if the probability that a random object chosen from the collection has that property is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Function
In mathematics, a real-valued function is called convex if the line segment between any two distinct points on the graph of a function, graph of the function lies above or on the graph between the two points. Equivalently, a function is convex if its epigraph (mathematics), ''epigraph'' (the set of points on or above the graph of the function) is a convex set. In simple terms, a convex function graph is shaped like a cup \cup (or a straight line like a linear function), while a concave function's graph is shaped like a cap \cap. A twice-differentiable function, differentiable function of a single variable is convex if and only if its second derivative is nonnegative on its entire domain of a function, domain. Well-known examples of convex functions of a single variable include a linear function f(x) = cx (where c is a real number), a quadratic function cx^2 (c as a nonnegative real number) and an exponential function ce^x (c as a nonnegative real number). Convex functions pl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Independent Set (graph Theory)
In graph theory, an independent set, stable set, coclique or anticlique is a set of vertices in a graph, no two of which are adjacent. That is, it is a set S of vertices such that for every two vertices in S, there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in S. A set is independent if and only if it is a clique in the graph's complement. The size of an independent set is the number of vertices it contains. Independent sets have also been called "internally stable sets", of which "stable set" is a shortening. A maximal independent set is an independent set that is not a proper subset of any other independent set. A maximum independent set is an independent set of largest possible size for a given graph G. This size is called the independence number of ''G'' and is usually denoted by \alpha(G). The optimization problem of finding such a set is called the maximum independent set problem. It is a strongly NP-hard problem. As ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Turán's Theorem
In graph theory, Turán's theorem bounds the number of edges that can be included in an undirected graph that does not have a clique (graph theory), complete subgraph of a given size. It is one of the central results of extremal graph theory, an area studying the largest or smallest graphs with given properties, and is a special case of the forbidden subgraph problem on the maximum number of edges in a graph that does not have a given subgraph. An example of an n-vertex (graph theory), vertex graph that does not contain any (r+1)-vertex clique K_ may be formed by partitioning the set of n vertices into r parts of equal or nearly equal size, and connecting two vertices by an edge whenever they belong to two different parts. The resulting graph is the Turán graph T(n,r). Turán's theorem states that the Turán graph has the largest number of edges among all -free -vertex graphs. Turán's theorem, and the Turán graphs giving its extreme case, were first described and studied by Hun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maximum Cut
In a graph, a maximum cut is a cut whose size is at least the size of any other cut. That is, it is a partition of the graph's vertices into two complementary sets and , such that the number of edges between and is as large as possible. Finding such a cut is known as the max-cut problem. The problem can be stated simply as follows. One wants a subset of the vertex set such that the number of edges between and the complementary subset is as large as possible. Equivalently, one wants a bipartite subgraph of the graph with as many edges as possible. There is a more general version of the problem called weighted max-cut, where each edge is associated with a real number, its weight, and the objective is to maximize the total weight of the edges between and its complement rather than the number of the edges. The weighted max-cut problem allowing both positive and negative weights can be trivially transformed into a weighted minimum cut problem by flipping the sign in all ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |