|
Medial Graph
In the mathematical discipline of graph theory, the medial graph of plane graph ''G'' is another graph ''M(G)'' that represents the adjacencies between edges in the faces of ''G''. Medial graphs were introduced in 1922 by Ernst Steinitz to study combinatorial properties of convex polyhedra, although the inverse construction was already used by Peter Tait in 1877 in his foundational study of knots and links. Formal definition Given a connected plane graph ''G'', its medial graph ''M(G)'' has * a vertex for each edge of ''G'' and * an edge between two vertices for each face of ''G'' in which their corresponding edges occur consecutively. The medial graph of a disconnected graph is the disjoint union of the medial graphs of each connected component. The definition of medial graph also extends without modification to graph embeddings on surfaces of higher genus. Properties * The medial graph of any plane graph is a 4- regular plane graph. * For any plane graph ''G'', the me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Medial Graph Example
Medial may refer to: Mathematics * Medial magma, a mathematical identity in algebra Geometry * Medial axis, in geometry the set of all points having more than one closest point on an object's boundary * Medial graph, another graph that represents the adjacencies between edges in the faces of a plane graph * Medial triangle, the triangle whose vertices lie at the midpoints of an enclosing triangle's sides * Polyhedra: ** Medial deltoidal hexecontahedron ** Medial disdyakis triacontahedron ** Medial hexagonal hexecontahedron ** Medial icosacronic hexecontahedron ** Medial inverted pentagonal hexecontahedron ** Medial pentagonal hexecontahedron ** Medial rhombic triacontahedron Linguistics * A medial sound or letter is one that is found in the middle of a larger unit (like a word) ** Syllable medial, a segment located between the onset and the rime of a syllable * In the older literature, a term for the voiced stops (like ''b'', ''d'', ''g'') * Medial or second person demon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Isomorphism
In graph theory, an isomorphism of graphs ''G'' and ''H'' is a bijection between the vertex sets of ''G'' and ''H'' : f \colon V(G) \to V(H) such that any two vertices ''u'' and ''v'' of ''G'' are adjacent in ''G'' if and only if f(u) and f(v) are adjacent in ''H''. This kind of bijection is commonly described as "edge-preserving bijection", in accordance with the general notion of isomorphism being a structure-preserving bijection. If an isomorphism exists between two graphs, then the graphs are called isomorphic and denoted as G\simeq H. In the case when the bijection is a mapping of a graph onto itself, i.e., when ''G'' and ''H'' are one and the same graph, the bijection is called an automorphism of ''G''. If a graph is finite, we can prove it to be bijective by showing it is one-one/onto; no need to show both. Graph isomorphism is an equivalence relation on graphs and as such it partitions the class of all graphs into equivalence classes. A set of graphs isomorphic to each ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Operations
In the mathematical field of graph theory, graph operations are operations which produce new graphs from initial ones. They include both unary (one input) and binary (two input) operations. Unary operations Unary operations create a new graph from a single initial graph. Elementary operations Elementary operations or editing operations, which are also known as graph edit operations, create a new graph from one initial one by a simple local change, such as addition or deletion of a vertex or of an edge, merging and splitting of vertices, edge contraction, etc. The graph edit distance between a pair of graphs is the minimum number of elementary operations required to transform one graph into the other. Advanced operations Advanced operations create a new graph from initial one by a complex changes, such as: * transpose graph; * complement graph; * line graph; * graph minor; * graph rewriting; * power of graph; * dual graph; * medial graph; * quotient graph; * Y-Δ transform; * My ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polyhedron
In geometry, a polyhedron (plural polyhedra or polyhedrons; ) is a three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices. A convex polyhedron is the convex hull of finitely many points, not all on the same plane. Cubes and pyramids are examples of convex polyhedra. A polyhedron is a 3-dimensional example of a polytope, a more general concept in any number of dimensions. Definition Convex polyhedra are well-defined, with several equivalent standard definitions. However, the formal mathematical definition of polyhedra that are not required to be convex has been problematic. Many definitions of "polyhedron" have been given within particular contexts,. some more rigorous than others, and there is not universal agreement over which of these to choose. Some of these definitions exclude shapes that have often been counted as polyhedra (such as the self-crossing polyhedra) or include shapes that are often not considered as valid polyhedr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rectification (geometry)
In Euclidean geometry, rectification, also known as critical truncation or complete-truncation, is the process of truncating a polytope by marking the midpoints of all its Edge (geometry), edges, and cutting off its Vertex (geometry), vertices at those points. The resulting polytope will be bounded by vertex figure facets and the rectified facets of the original polytope. A rectification operator is sometimes denoted by the letter with a Schläfli symbol. For example, is the rectified cube, also called a cuboctahedron, and also represented as \begin 4 \\ 3 \end. And a rectified cuboctahedron is a rhombicuboctahedron, and also represented as r\begin 4 \\ 3 \end. Conway polyhedron notation uses for ambo as this operator. In graph theory this operation creates a medial graph. The rectification of any regular self-dual polyhedron or tiling will result in another regular polyhedron or tiling with a tiling order of 4, for example the tetrahedron becoming an octahedron As a s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tait Graph
Tait may refer to: * Tait (band), an American Christian rock band formed by Michael Tait * Tait (train) The Tait trains were a wooden bodied Electric Multiple Unit train that operated on the suburban railway network of Melbourne, Victoria, Australia. They were introduced in 1910 by the Victorian Railways as steam locomotive hauled cars, and con ..., a type of train that operated in and near Melbourne, Australia * Tait or Honey possum, a small marsupial (mammal) of Australia * Tait Communications, a radio communications company * Tait Glacier, a glacier on James Ross Island, Antarctica * Tait River, a river in Minnesota, United States People *Tait (surname), a surname (including a list of people with the surname) People with the given name * Tait Fletcher, American mixed martial artist See also * * Tate (other) {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Knots And Graphs
In mathematics, a knot is an embedding of the circle into three-dimensional Euclidean space, (also known as ). Often two knots are considered equivalent if they are ambient isotopic, that is, if there exists a continuous deformation of which takes one knot to the other. A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed — there are no ends to tie or untie on a mathematical knot. Physical properties such as friction and thickness also do not apply, although there are mathematical definitions of a knot that take such properties into account. The term ''knot'' is also applied to embeddings of in , especially in the case . The branch of mathematics that studies knots is known as knot theory and has many relations to graph theory. Formal definition A knot is an embedding of the circle () into three-dimensional Euclidean space (), or the 3-sphere (), since the 3-sphere is compact. Two knots a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
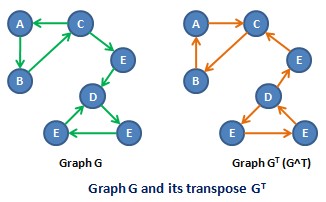
Transpose Graph
In the mathematical and algorithmic study of graph theory, the converse, transpose or reverse, entry 2.24 of a directed graph is another directed graph on the same set of vertices with all of the edges reversed compared to the orientation of the corresponding edges in . That is, if contains an edge then the converse/transpose/reverse of contains an edge and vice versa. Notation The name arises because the reversal of arrows corresponds to taking the converse of an implication in logic. The name is because the adjacency matrix of the transpose directed graph is the transpose of the adjacency matrix of the original directed graph. There is no general agreement on preferred terminology. The converse is denoted symbolically as , , , or other notations, depending on which terminology is used and which book or article is the source for the notation. Applications Although there is little difference mathematically between a graph and its transpose, the difference may be lar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Directed Medial Graph Example
Director may refer to: Literature * ''Director'' (magazine), a British magazine * ''The Director'' (novel), a 1971 novel by Henry Denker * ''The Director'' (play), a 2000 play by Nancy Hasty Music * Director (band), an Irish rock band * ''Director'' (Avant album) (2006) * ''Director'' (Yonatan Gat album) Occupations and positions Arts and design * Animation director * Artistic director * Creative director * Design director * Film director * Music director * Music video director * Sports director * Television director * Theatre director Positions in other fields * Director (business), a senior level management position * Director (colonial), head of chartered company's colonial administration in a territory * Director (education), head of a university or other educational body * Company director * Cruise director * Executive director * Finance director or chief financial officer * Funeral director * Managing director * Non-executive director * Technical director * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eulerian Orientation
In graph theory, an Eulerian trail (or Eulerian path) is a trail in a finite graph that visits every edge exactly once (allowing for revisiting vertices). Similarly, an Eulerian circuit or Eulerian cycle is an Eulerian trail that starts and ends on the same vertex. They were first discussed by Leonhard Euler while solving the famous Seven Bridges of Königsberg problem in 1736. The problem can be stated mathematically like this: :Given the graph in the image, is it possible to construct a path (or a cycle; i.e., a path starting and ending on the same vertex) that visits each edge exactly once? Euler proved that a necessary condition for the existence of Eulerian circuits is that all vertices in the graph have an even degree, and stated without proof that connected graphs with all vertices of even degree have an Eulerian circuit. The first complete proof of this latter claim was published posthumously in 1873 by Carl Hierholzer. This is known as Euler's Theorem: :A connected gr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tutte Polynomial
The Tutte polynomial, also called the dichromate or the Tutte–Whitney polynomial, is a graph polynomial. It is a polynomial in two variables which plays an important role in graph theory. It is defined for every undirected graph G and contains information about how the graph is connected. It is denoted by T_G. The importance of this polynomial stems from the information it contains about G. Though originally studied in algebraic graph theory as a generalization of counting problems related to graph coloring and nowhere-zero flow, it contains several famous other specializations from other sciences such as the Jones polynomial from knot theory and the partition functions of the Potts model from statistical physics. It is also the source of several central computational problems in theoretical computer science. The Tutte polynomial has several equivalent definitions. It is equivalent to Whitney’s rank polynomial, Tutte’s own dichromatic polynomial and Fortuin–Kasteleyn ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Line Graph
In the mathematical discipline of graph theory, the line graph of an undirected graph is another graph that represents the adjacencies between edges of . is constructed in the following way: for each edge in , make a vertex in ; for every two edges in that have a vertex in common, make an edge between their corresponding vertices in . The name line graph comes from a paper by although both and used the construction before this. Other terms used for the line graph include the covering graph, the derivative, the edge-to-vertex dual, the conjugate, the representative graph, and the θ-obrazom, as well as the edge graph, the interchange graph, the adjoint graph, and the derived graph., p. 71. proved that with one exceptional case the structure of a connected graph can be recovered completely from its line graph. Many other properties of line graphs follow by translating the properties of the underlying graph from vertices into edges, and by Whitney's theorem the same t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
