|
Madhava Series
In mathematics, a Madhava series or Leibniz series is any one of the series in a collection of infinite series expressions all of which are believed to have been discovered by an Indian Mathematician and Astronomer Madhava of Sangamagrama (c. 1350 – c. 1425), the founder of the Kerala school of astronomy and mathematics and later by Gottfried Wilhelm Leibniz, among others. These expressions are the Maclaurin series expansions of the trigonometric sine, cosine and arctangent functions, and the special case of the power series expansion of the arctangent function yielding a formula for computing . The power series expansions of sine and cosine functions are respectively called ''Madhava's sine series'' and ''Madhava's cosine series''. The power series expansion of the arctangent function is sometimes called ''Madhava–Gregory series'' or ''Gregory–Madhava series''. These power series are also collectively called ''Taylor–Madhava series''. The formula for is ref ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tantrasamgraha
Tantrasamgraha, or Tantrasangraha, (literally, ''A Compilation of the System'') is an important astronomical treatise written by Nilakantha Somayaji, an astronomer/ mathematician belonging to the Kerala school of astronomy and mathematics. The treatise was completed in 1501 CE. It consists of 432 verses in Sanskrit divided into eight chapters. Tantrasamgraha had spawned a few commentaries: ''Tantrasamgraha-vyakhya'' of anonymous authorship and '' Yuktibhāṣā'' authored by Jyeshtadeva in about 1550 CE. Tantrasangraha, together with its commentaries, bring forth the depths of the mathematical accomplishments the Kerala school of astronomy and mathematics, in particular the achievements of the remarkable mathematician of the school Sangamagrama Madhava. In his ''Tantrasangraha'', Nilakantha revised Aryabhata's model for the planets Mercury and Venus. His equation of the centre for these planets remained the most accurate until the time of Johannes Kepler in the 17th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Puiseux Series
In mathematics, Puiseux series are a generalization of power series that allow for negative and fractional exponents of the indeterminate. For example, the series : \begin x^ &+ 2x^ + x^ + 2x^ + x^ + x^5 + \cdots\\ &=x^+ 2x^ + x^ + 2x^ + x^ + x^ + \cdots \end is a Puiseux series in the indeterminate . Puiseux series were first introduced by Isaac Newton in 1676 and rediscovered by Victor Puiseux in 1850.Puiseux (1850, 1851) The definition of a Puiseux series includes that the denominators of the exponents must be bounded. So, by reducing exponents to a common denominator , a Puiseux series becomes a Laurent series in a th root of the indeterminate. For example, the example above is a Laurent series in x^. Because a complex number has th roots, a convergent Puiseux series typically defines functions in a neighborhood of . Puiseux's theorem, sometimes also called the Newton–Puiseux theorem, asserts that, given a polynomial equation P(x,y)=0 with complex coefficients ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laurent Series
In mathematics, the Laurent series of a complex function f(z) is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where a Taylor series expansion cannot be applied. The Laurent series was named after and first published by Pierre Alphonse Laurent in 1843. Karl Weierstrass may have discovered it first in a paper written in 1841, but it was not published until after his death.. Definition The Laurent series for a complex function f(z) about a point c is given by f(z) = \sum_^\infty a_n(z-c)^n, where a_n and c are constants, with a_n defined by a line integral that generalizes Cauchy's integral formula: a_n =\frac\oint_\gamma \frac \, dz. The path of integration \gamma is counterclockwise around a Jordan curve enclosing c and lying in an annulus A in which f(z) is holomorphic (analytic). The expansion for f(z) will then be valid anywhere inside the annulus. The annulus is shown in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor Series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor series are named after Brook Taylor, who introduced them in 1715. A Taylor series is also called a Maclaurin series, when 0 is the point where the derivatives are considered, after Colin Maclaurin, who made extensive use of this special case of Taylor series in the mid-18th century. The partial sum formed by the first terms of a Taylor series is a polynomial of degree that is called the th Taylor polynomial of the function. Taylor polynomials are approximations of a function, which become generally better as increases. Taylor's theorem gives quantitative estimates on the error introduced by the use of such approximations. If the Taylor series of a function is convergent, its sum is the limit of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Padé Approximant
In mathematics, a Padé approximant is the "best" approximation of a function near a specific point by a rational function of given order. Under this technique, the approximant's power series agrees with the power series of the function it is approximating. The technique was developed around 1890 by Henri Padé, but goes back to Georg Frobenius, who introduced the idea and investigated the features of rational approximations of power series. The Padé approximant often gives better approximation of the function than truncating its Taylor series, and it may still work where the Taylor series does not converge. For these reasons Padé approximants are used extensively in computer calculations. They have also been used as auxiliary functions in Diophantine approximation and transcendental number theory, though for sharp results ad hoc methods— in some sense inspired by the Padé theory— typically replace them. Since Padé approximant is a rational function, an artificial s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
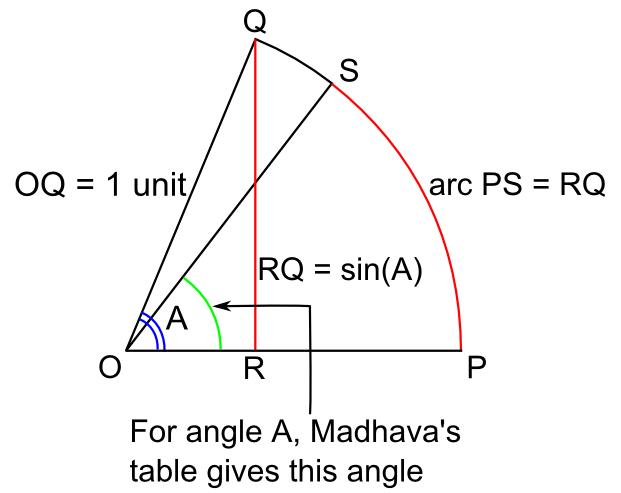
Madhava's Sine Table
Madhava's sine table is the table of trigonometric sines of various angles constructed by the 14th century Kerala mathematician-astronomer Madhava of Sangamagrama. The table lists the trigonometric sines of the twenty-four angles 3.75°, 7.50°, 11.25°, ..., and 90.00° (angles that are integral multiples of 3.75°, i.e. 1/24 of a right angle, beginning with 3.75 and ending with 90.00). The table is encoded in the letters of Devanagari using the Katapayadi system. This gives the entries in the table an appearance of the verses of a poem in Sanskrit. Madhava's original work containing the sine table has not yet been traced. The table is seen reproduced in the ''Aryabhatiyabhashya'' of Nilakantha Somayaji''The Aryabhatiam of Aryabhattacharya with the Bhashya of Nilakantha Somasutvan, Part1-Gaṇitapāda,'' Edited by K. Sambasiva Sastri, Trivandrum Sanskrit Series No.101. p. 55. https://archive.org/details/Trivandrum_Sanskrit_Series_TSS http://www.sanskritebooks.org/2013/0 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Katapayadi System
''Kaṭapayādi'' system (Devanagari: कटपयादि, also known as ''Paralppēru'', Malayalam: പരല്പ്പേര്) of numerical notation is an ancient Indian alphasyllabic numeral system to depict letters to numerals for easy remembrance of numbers as words or verses. Assigning more than one letter to one numeral and nullifying certain other letters as valueless, this system provides the flexibility in forming meaningful words out of numbers which can be easily remembered. History The oldest available evidence of the use of ''Kaṭapayādi'' (Sanskrit: कटपयादि) system is from ''Grahacāraṇibandhana'' by Haridatta in 683 CE.Sreeramamula Rajeswara Sarma, THE ''KATAPAYADI'' SYSTEM OF NUMERICAL NOTATION AND ITS SPREAD OUTSIDE KERALA, ''Rev. d'Histoire de Mathmatique'' 18 (2012/ref> It has been used in ''Laghu·bhāskarīya·vivaraṇa'' written by '' Sankara Narayana, Śaṅkara·nārāyaṇa'' in 869 CE. Some argue that the system orig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |