|
Log-rank Test
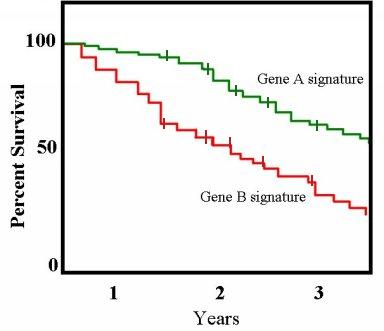
The logrank test, or log-rank test, is a hypothesis test to compare the survival distributions of two samples. It is a nonparametric test and appropriate to use when the data are right skewed and censored (technically, the censoring must be non-informative). It is widely used in clinical trials to establish the efficacy of a new treatment in comparison with a control treatment when the measurement is the time to event (such as the time from initial treatment to a heart attack). The test is sometimes called the Mantel–Cox test. The logrank test can also be viewed as a time-stratified Cochran–Mantel–Haenszel test. The test was first proposed by Nathan Mantel and was named the ''logrank test'' by Richard and Julian Peto. Definition The logrank test statistic compares estimates of the hazard functions of the two groups at each observed event time. It is constructed by computing the observed and expected number of events in one of the groups at each observed event time and t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hypothesis Test
A statistical hypothesis test is a method of statistical inference used to decide whether the data at hand sufficiently support a particular hypothesis. Hypothesis testing allows us to make probabilistic statements about population parameters. History Early use While hypothesis testing was popularized early in the 20th century, early forms were used in the 1700s. The first use is credited to John Arbuthnot (1710), followed by Pierre-Simon Laplace (1770s), in analyzing the human sex ratio at birth; see . Modern origins and early controversy Modern significance testing is largely the product of Karl Pearson (p-value, ''p''-value, Pearson's chi-squared test), William Sealy Gosset (Student's t-distribution), and Ronald Fisher ("null hypothesis", analysis of variance, "statistical significance, significance test"), while hypothesis testing was developed by Jerzy Neyman and Egon Pearson (son of Karl). Ronald Fisher began his life in statistics as a Bayesian (Zabell 1992), but Fisher ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Central Limit Theorem
In probability theory, the central limit theorem (CLT) establishes that, in many situations, when independent random variables are summed up, their properly normalized sum tends toward a normal distribution even if the original variables themselves are not normally distributed. The theorem is a key concept in probability theory because it implies that probabilistic and statistical methods that work for normal distributions can be applicable to many problems involving other types of distributions. This theorem has seen many changes during the formal development of probability theory. Previous versions of the theorem date back to 1811, but in its modern general form, this fundamental result in probability theory was precisely stated as late as 1920, thereby serving as a bridge between classical and modern probability theory. If X_1, X_2, \dots, X_n, \dots are random samples drawn from a population with overall mean \mu and finite variance and if \bar_n is the sample mean of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hazard Ratio
In survival analysis, the hazard ratio (HR) is the ratio of the hazard rates corresponding to the conditions characterised by two distinct levels of a treatment variable of interest. For example, in a clinical study of a drug, the treated population may die at twice the rate per unit time of the control population. The hazard ratio would be 2, indicating higher hazard of death from the treatment. A scientific paper might utilise a Hazard Ratio (HR) to state something as follows. "Adequate COVID-19 vaccination status was associated with significantly decreased risk for the composite of severe COVID-19 or mortality with a HR of 0.20 (95% CI, 0.17-0.22)." In layman's English, this means: People in the study who were vaccinated were 20% as likely to get severe Covid-19 or to die, compared to people who weren't vaccinated in the same study. So, for a hazardous outcome (e.g. death), a Hazard Ratio below 1 indicates that the treatment (e.g. vaccination) might be favorable (less hazardous ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kaplan–Meier Estimator
The Kaplan–Meier estimator, also known as the product limit estimator, is a non-parametric statistic used to estimate the survival function from lifetime data. In medical research, it is often used to measure the fraction of patients living for a certain amount of time after treatment. In other fields, Kaplan–Meier estimators may be used to measure the length of time people remain unemployed after a job loss, the time-to-failure of machine parts, or how long fleshy fruits remain on plants before they are removed by frugivores. The estimator is named after Edward L. Kaplan and Paul Meier, who each submitted similar manuscripts to the ''Journal of the American Statistical Association''. The journal editor, John Tukey, convinced them to combine their work into one paper, which has been cited almost 61,000 times since its publication in 1958. The estimator of the survival function S(t) (the probability that life is longer than t) is given by: : \widehat S(t) = \prod\limits_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Peto Logrank Test
Peto may refer to: People * Peto (surname), includes a list of people with the surname Peto * Kawu Peto Dukku (1958–2010), Nigerian politician, Senator for the Gombe North constituency of Gombe State, Nigeria Other uses *PETO, a German party * Peto (food), a Colombian dessert * USS ''Peto'' (SS-265), a US submarine * Parnall Peto, a British seaplane * Peto baronets, two baronetcies created for members of the Peto family, both in the Baronetage of the United Kingdom * Peto, Yucatán, a town *Peto Municipality in Yucatán state, Mexico *A minor character who appears in the Henriad plays by Shakespeare as a criminal associate of Falstaff * Grissell and Peto, a civil engineering partnership between Thomas Grissell and his cousin Morton Peto *Peto, Brassey and Betts Peto, Brassey and Betts was a civil engineering partnership between Samuel Morton Peto, Thomas Brassey and Edward Betts. They built a supply and casualty transport railway ( Grand Crimean Central Railway) from Bala ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wilcoxon Rank Sum Test
Wilcoxon is a surname, and may refer to: * Charles Wilcoxon, drum educator * Henry Wilcoxon, an actor * Frank Wilcoxon, chemist and statistician, inventor of two non-parametric tests for statistical significance In statistical hypothesis testing, a result has statistical significance when it is very unlikely to have occurred given the null hypothesis (simply by chance alone). More precisely, a study's defined significance level, denoted by \alpha, is the p ...: ** The Wilcoxon signed-rank test (also known as the Wilcoxon T test) ** The Wilcoxon rank-sum test (also known as the Mann–Whitney U test). See also * Wilcox (surname) {{surname ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Distribution
In probability theory and statistics, the exponential distribution is the probability distribution of the time between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate. It is a particular case of the gamma distribution. It is the continuous analogue of the geometric distribution, and it has the key property of being memoryless. In addition to being used for the analysis of Poisson point processes it is found in various other contexts. The exponential distribution is not the same as the class of exponential families of distributions. This is a large class of probability distributions that includes the exponential distribution as one of its members, but also includes many other distributions, like the normal, binomial, gamma, and Poisson distributions. Definitions Probability density function The probability density function (pdf) of an exponential distribution is : f(x;\lambda) = \begin \lambda ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Likelihood Ratio Test
In statistics, the likelihood-ratio test assesses the goodness of fit of two competing statistical models based on the ratio of their likelihoods, specifically one found by maximization over the entire parameter space and another found after imposing some constraint. If the constraint (i.e., the null hypothesis) is supported by the observed data, the two likelihoods should not differ by more than sampling error. Thus the likelihood-ratio test tests whether this ratio is significantly different from one, or equivalently whether its natural logarithm is significantly different from zero. The likelihood-ratio test, also known as Wilks test, is the oldest of the three classical approaches to hypothesis testing, together with the Lagrange multiplier test and the Wald test. In fact, the latter two can be conceptualized as approximations to the likelihood-ratio test, and are asymptotically equivalent. In the case of comparing two models each of which has no unknown parameters, use o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proportional Hazards Models
Proportional hazards models are a class of survival models in statistics. Survival models relate the time that passes, before some event occurs, to one or more covariates that may be associated with that quantity of time. In a proportional hazards model, the unique effect of a unit increase in a covariate is multiplicative with respect to the hazard rate. For example, taking a drug may halve one's hazard rate for a stroke occurring, or, changing the material from which a manufactured component is constructed may double its hazard rate for failure. Other types of survival models such as accelerated failure time models do not exhibit proportional hazards. The accelerated failure time model describes a situation where the biological or mechanical life history of an event is accelerated (or decelerated). Background Survival models can be viewed as consisting of two parts: the underlying baseline hazard function, often denoted \lambda_0(t), describing how the risk of event per time ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Score Test
In statistics, the score test assesses constraints on statistical parameters based on the gradient of the likelihood function—known as the ''score''—evaluated at the hypothesized parameter value under the null hypothesis. Intuitively, if the restricted estimator is near the maximum of the likelihood function, the score should not differ from zero by more than sampling error. While the finite sample distributions of score tests are generally unknown, they have an asymptotic χ2-distribution under the null hypothesis as first proved by C. R. Rao in 1948, a fact that can be used to determine statistical significance. Since function maximization subject to equality constraints is most conveniently done using a Lagrangean expression of the problem, the score test can be equivalently understood as a test of the magnitude of the Lagrange multipliers associated with the constraints where, again, if the constraints are non-binding at the maximum likelihood, the vector of Lagrange mu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hypergeometric Distribution
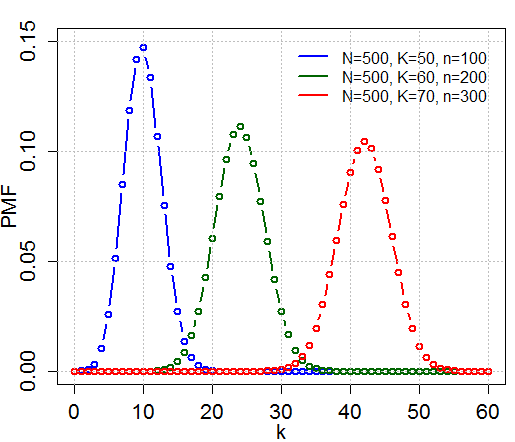
In probability theory and statistics, the hypergeometric distribution is a discrete probability distribution that describes the probability of k successes (random draws for which the object drawn has a specified feature) in n draws, ''without'' replacement, from a finite population of size N that contains exactly K objects with that feature, wherein each draw is either a success or a failure. In contrast, the binomial distribution describes the probability of k successes in n draws ''with'' replacement. Definitions Probability mass function The following conditions characterize the hypergeometric distribution: * The result of each draw (the elements of the population being sampled) can be classified into one of two mutually exclusive categories (e.g. Pass/Fail or Employed/Unemployed). * The probability of a success changes on each draw, as each draw decreases the population (''sampling without replacement'' from a finite population). A random variable X follows the hyperg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |