|
Linear Canonical Transform
In Hamiltonian mechanics, the linear canonical transformation (LCT) is a family of integral transforms that generalizes many classical transforms. It has 4 parameters and 1 constraint, so it is a 3-dimensional family, and can be visualized as the action of the special linear group SL2(R) on the time–frequency plane (domain). As this defines the original function up to a sign, this translates into an action of its double cover on the original function space. The LCT generalizes the Fourier, fractional Fourier, Laplace, Gauss–Weierstrass, Bargmann and the Fresnel transforms as particular cases. The name "linear canonical transformation" is from canonical transformation, a map that preserves the symplectic structure, as SL2(R) can also be interpreted as the symplectic group Sp2, and thus LCTs are the linear maps of the time–frequency domain which preserve the symplectic form, and their action on the Hilbert space is given by the Metaplectic group. The basic properties of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamiltonian Mechanics
Hamiltonian mechanics emerged in 1833 as a reformulation of Lagrangian mechanics. Introduced by Sir William Rowan Hamilton, Hamiltonian mechanics replaces (generalized) velocities \dot q^i used in Lagrangian mechanics with (generalized) ''momenta''. Both theories provide interpretations of classical mechanics and describe the same physical phenomena. Hamiltonian mechanics has a close relationship with geometry (notably, symplectic geometry and Poisson structures) and serves as a link between classical and quantum mechanics. Overview Phase space coordinates (p,q) and Hamiltonian H Let (M, \mathcal L) be a mechanical system with the configuration space M and the smooth Lagrangian \mathcal L. Select a standard coordinate system (\boldsymbol,\boldsymbol) on M. The quantities \textstyle p_i(\boldsymbol,\boldsymbol,t) ~\stackrel~ / are called ''momenta''. (Also ''generalized momenta'', ''conjugate momenta'', and ''canonical momenta''). For a time instant t, the Legendre transformat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional Laplace Transform
A fraction is one or more equal parts of something. Fraction may also refer to: * Fraction (chemistry), a quantity of a substance collected by fractionation * Fraction (floating point number), an (ambiguous) term sometimes used to specify a part of a floating point number * Fraction (politics), a subgroup within a parliamentary party * Fraction (radiation therapy), one unit of treatment of the total radiation dose of radiation therapy that is split into multiple treatment sessions * Fraction (religion), the ceremonial act of breaking the bread during Christian Communion People with the surname * Matt Fraction, a comic book author See also * Algebraic fraction, an indicated division in which the divisor, or both dividend and divisor, are algebraic expressions ** Irrational fraction, a type of algebraic fraction * Faction (other) * ''Frazione'', a type of administrative division of an Italian ''commune'' * Free and Independent Fraction, a Romanian political party * Part (d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave Number
In the physical sciences, the wavenumber (also wave number or repetency) is the ''spatial frequency'' of a wave, measured in cycles per unit distance (ordinary wavenumber) or radians per unit distance (angular wavenumber). It is analogous to temporal frequency, which is defined as the number of wave cycles per unit time (''ordinary frequency'') or radians per unit time (''angular frequency''). In multidimensional systems, the wavenumber is the magnitude of the ''wave vector''. The space of wave vectors is called ''reciprocal space''. Wave numbers and wave vectors play an essential role in optics and the physics of wave scattering, such as X-ray diffraction, neutron diffraction, electron diffraction, and elementary particle physics. For quantum mechanical waves, the wavenumber multiplied by the reduced Planck's constant is the ''canonical momentum''. Wavenumber can be used to specify quantities other than spatial frequency. For example, in optical spectroscopy, it is often used a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
TFA LCT Fresnel
TFA may refer to: * Task Force Argos, responsible for investigation of online child exploitation and abuse * Taipei Football Association * Tata Football Academy, a football (soccer) organisation in India * Taxpayer First Act, an IRS reform law * Teach For America, an organization to recruit teachers for public schools * Technology Futures Analysis, a collective term from futures studies * Terengganu FA, a Malaysian football club * Texas Forensic Association, an organization that provides speech and debate competitions for school students * The Freedom Association, a free-market libertarian advocacy group in the United Kingdom * Time–frequency analysis, a signal processing approach utilizing both time and frequency components of a signal * Trade Facilitation Agreement, part of the 2013 WTO Bali Package * Trans fatty acid * Trifluoroacetic acid, a strong carboxylic acid * Trifluoroacetone, a chemical compound * Two-factor authentication Multi-factor authentication (MFA; encom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fokker–Planck Equation
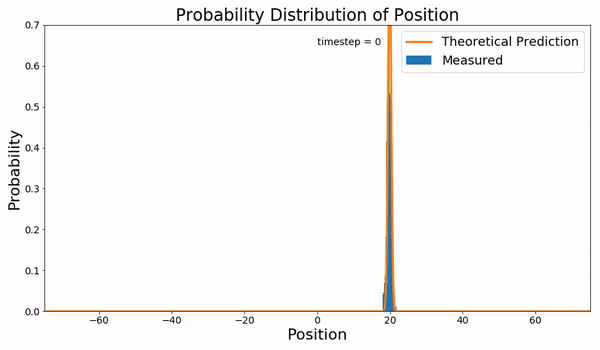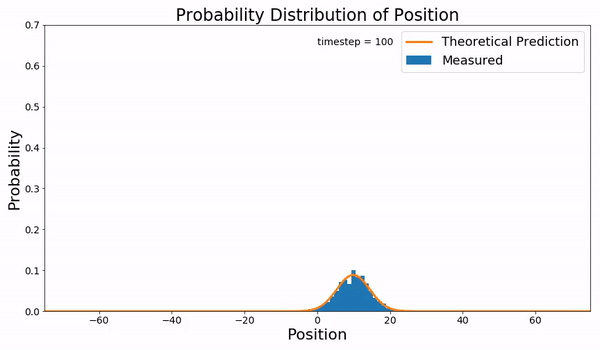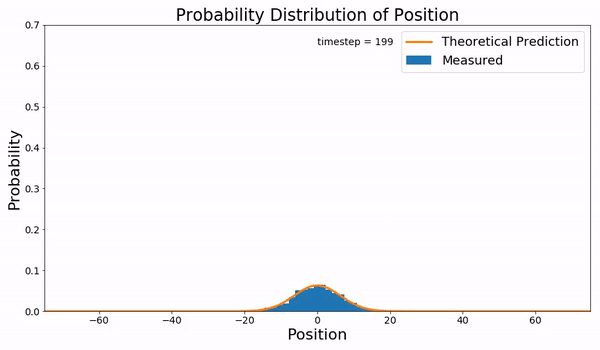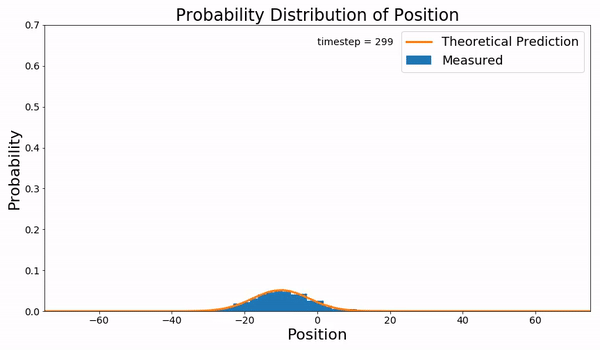
In statistical mechanics, the Fokker–Planck equation is a partial differential equation that describes the time evolution of the probability density function of the velocity of a particle under the influence of drag forces and random forces, as in Brownian motion. The equation can be generalized to other observables as well. It is named after Adriaan Fokker and Max Planck, who described it in 1914 and 1917. It is also known as the Kolmogorov forward equation, after Andrey Kolmogorov, who independently discovered it in 1931. When applied to particle position distributions, it is better known as the Smoluchowski equation (after Marian Smoluchowski), and in this context it is equivalent to the convection–diffusion equation. The case with zero diffusion is the continuity equation. The Fokker–Planck equation is obtained from the master equation through Kramers–Moyal expansion. The first consistent microscopic derivation of the Fokker–Planck equation in the single schem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Free Particle
In physics, a free particle is a particle that, in some sense, is not bound by an external force, or equivalently not in a region where its potential energy varies. In classical physics, this means the particle is present in a "field-free" space. In quantum mechanics, it means the particle is in a region of uniform potential, usually set to zero in the region of interest since the potential can be arbitrarily set to zero at any point in space. Classical free particle The classical free particle is characterized by a fixed velocity v. The momentum is given by \mathbf=m\mathbf and the kinetic energy (equal to total energy) by E=\fracmv^2=\frac where ''m'' is the mass of the particle and v is the vector velocity of the particle. Quantum free particle Mathematical description A free particle with mass m in non-relativistic quantum mechanics is described by the free Schrödinger equation: - \frac \nabla^2 \ \psi(\mathbf, t) = i\hbar\frac \psi (\mathbf, t) where ''ψ'' is the wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffusion
Diffusion is the net movement of anything (for example, atoms, ions, molecules, energy) generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, like in spinodal decomposition. The concept of diffusion is widely used in many fields, including physics (particle diffusion), chemistry, biology, sociology, economics, and finance (diffusion of people, ideas, and price values). The central idea of diffusion, however, is common to all of these: a substance or collection undergoing diffusion spreads out from a point or location at which there is a higher concentration of that substance or collection. A gradient is the change in the value of a quantity, for example, concentration, pressure, or temperature with the change in another variable, usually distance. A change in c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Canonical Commutation Relation
In quantum mechanics, the canonical commutation relation is the fundamental relation between canonical conjugate quantities (quantities which are related by definition such that one is the Fourier transform of another). For example, hat x,\hat p_x= i\hbar \mathbb between the position operator and momentum operator in the direction of a point particle in one dimension, where is the commutator of and , is the imaginary unit, and is the reduced Planck's constant , and \mathbb is the unit operator. In general, position and momentum are vectors of operators and their commutation relation between different components of position and momentum can be expressed as hat r_i,\hat p_j= i\hbar \delta_ \mathbb. where \delta_ is the Kronecker delta. This relation is attributed to Werner Heisenberg, Max Born and Pascual Jordan (1925), who called it a "quantum condition" serving as a postulate of the theory; it was noted by E. Kennard (1927) to imply the Heisenberg uncertainty principl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Position Operator
In quantum mechanics, the position operator is the operator that corresponds to the position observable of a particle. When the position operator is considered with a wide enough domain (e.g. the space of tempered distributions), its eigenvalues are the possible position vectors of the particle. In one dimension, if by the symbol , x \rangle we denote the unitary eigenvector of the position operator corresponding to the eigenvalue x, then, , x \rangle represents the state of the particle in which we know with certainty to find the particle itself at position x. Therefore, denoting the position operator by the symbol X in the literature we find also other symbols for the position operator, for instance Q (from Lagrangian mechanics), \hat \mathrm x and so on we can write X, x\rangle = x , x\rangle, for every real position x. One possible realization of the unitary state with position x is the Dirac delta (function) distribution centered at the position x, often denoted by \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Momentum Operator
In quantum mechanics, the momentum operator is the operator (physics), operator associated with the momentum (physics), linear momentum. The momentum operator is, in the position representation, an example of a differential operator. For the case of one particle in one spatial dimension, the definition is: \hat = - i \hbar \frac where is Planck's reduced constant, the imaginary unit, is the spatial coordinate, and a partial derivative (denoted by \partial/\partial x) is used instead of a total derivative () since the wave function is also a function of time. The "hat" indicates an operator. The "application" of the operator on a differentiable wave function is as follows: \hat\psi = - i \hbar \frac In a basis of Hilbert space consisting of momentum eigenstates expressed in the momentum representation, the action of the operator is simply multiplication by , i.e. it is a multiplication operator, just as the position operator is a multiplication operator in the position represen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science. Classical physics, the collection of theories that existed before the advent of quantum mechanics, describes many aspects of nature at an ordinary (macroscopic) scale, but is not sufficient for describing them at small (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation valid at large (macroscopic) scale. Quantum mechanics differs from classical physics in that energy, momentum, angular momentum, and other quantities of a bound system are restricted to discrete values ( quantization); objects have characteristics of both particles and waves (wave–particle duality); and there are limits to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thin Lens
In optics, a thin lens is a lens with a thickness (distance along the optical axis between the two surfaces of the lens) that is negligible compared to the radii of curvature of the lens surfaces. Lenses whose thickness is not negligible are sometimes called ''thick lenses''. The thin lens approximation ignores optical effects due to the thickness of lenses and simplifies ray tracing calculations. It is often combined with the paraxial approximation in techniques such as ray transfer matrix analysis. Focal length The focal length, ''f'', of a lens in air is given by the lensmaker's equation: :\frac = (n-1) \left \frac - \frac + \frac \right where ''n'' is the index of refraction of the lens material, and ''R''1 and ''R''2 are the radii of curvature of the two surfaces. For a thin lens, ''d'' is much smaller than one of the radii of curvature (either ''R''1 or ''R''2). In these conditions, the last term of the Lensmaker's equation becomes negligible, and the focal length of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |