|
Leximin
In mathematics, leximin order is a total preorder on finite-dimensional vectors. A more accurate, but less common term is leximin preorder. The leximin order is particularly important in social choice theory and fair division. Definition A vector x = (''x''1, ..., ''x''''n'') is ''leximin-larger'' than a vector y = (''y''1, ..., ''y''''n'') if one of the following holds: * The smallest element of x is larger than the smallest element of y; * The smallest elements of both vectors are equal, and the second-smallest element of x is larger than the second-smallest element of y; * ... * The ''k'' smallest elements of both vectors are equal, and the (''k''+1)-smallest element of x is larger than the (''k''+1)-smallest element of y. Examples The vector (3,5,3) is leximin-larger than (4,2,4), since the smallest element in the former is 3 and in the latter is 2. The vector (4,2,4) is leximin-larger than (5,3,2), since the smallest elements in both are 2, but the second-smallest ele ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leximin Item Allocation
Egalitarian item allocation, also called max-min item allocation is a fair item allocation problem, in which the fairness criterion follows the egalitarian rule. The goal is to maximize the minimum value of an agent. That is, among all possible allocations, the goal is to find an allocation in which the smallest value of an agent is as large as possible. In case there are two or more allocations with the same smallest value, then the goal is to select, from among these allocations, the one in which the second-smallest value is as large as possible, and so on (by the leximin order). Therefore, an egalitarian item allocation is sometimes called a leximin item allocation. The special case in which the value of each item ''j'' to each agent is either 0 or some constant ''vj'' is called the santa claus problem: santa claus has a fixed set of gifts, and wants to allocate them among children such that the least-happy child is as happy as possible. Some related problems are: * ''Multi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leximin Cake-cutting
Egalitarian cake-cutting is a kind of fair cake-cutting in which the fairness criterion is the egalitarian rule. The ''cake'' represents a continuous resource (such as land or time), that has to be allocated among people with different valuations over parts of the resource. The goal in egalitarian cake-cutting is to maximize the smallest value of an agent; subject to this, maximize the next-smallest value; and so on. It is also called leximin cake-cutting, since the optimization is done using the leximin order on the vectors of utilities. The concept of egalitarian cake-cutting was first described by Dubins and Spanier, who called it "optimal partition". Existence Leximin-optimal allocations exist whenever the set of allocations is a compact space. This is always the case when allocating discrete objects, and easy to prove when allocating a finite number of continuous homogeneous resources. Dubins and Spanier proved that, with a continuous ''heterogeneous'' resource ("cake"), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Egalitarian Rule
In social choice and operations research, the egalitarian rule (also called the max-min rule or the Rawlsian rule) is a rule saying that, among all possible alternatives, society should pick the alternative which maximizes the ''minimum utility'' of all individuals in society. It is a formal mathematical representation of the egalitarian philosophy. It also corresponds to John Rawls' principle of maximizing the welfare of the worst-off individual. Definition Let X be a set of possible `states of the world' or `alternatives'. Society wishes to choose a single state from X. For example, in a single-winner election, X may represent the set of candidates; in a resource allocation setting, X may represent all possible allocations. Let I be a finite set, representing a collection of individuals. For each i \in I, let u_i:X\longrightarrow\mathbb be a ''utility function'', describing the amount of happiness an individual ''i'' derives from each possible state. A '' social choice rule' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Total Preorder
In mathematics, especially order theory, a weak ordering is a mathematical formalization of the intuitive notion of a ranking of a set, some of whose members may be tied with each other. Weak orders are a generalization of totally ordered sets (rankings without ties) and are in turn generalized by partially ordered sets and preorders.. There are several common ways of formalizing weak orderings, that are different from each other but cryptomorphic (interconvertable with no loss of information): they may be axiomatized as strict weak orderings (partially ordered sets in which incomparability is a transitive relation), as total preorders (transitive binary relations in which at least one of the two possible relations exists between every pair of elements), or as ordered partitions ( partitions of the elements into disjoint subsets, together with a total order on the subsets). In many cases another representation called a preferential arrangement based on a utility function is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optimization Problem
In mathematics, computer science and economics, an optimization problem is the problem of finding the ''best'' solution from all feasible solutions. Optimization problems can be divided into two categories, depending on whether the variables are continuous or discrete: * An optimization problem with discrete variables is known as a '' discrete optimization'', in which an object such as an integer, permutation or graph must be found from a countable set. * A problem with continuous variables is known as a '' continuous optimization'', in which an optimal value from a continuous function must be found. They can include constrained problems and multimodal problems. Continuous optimization problem The '' standard form'' of a continuous optimization problem is \begin &\underset& & f(x) \\ &\operatorname & &g_i(x) \leq 0, \quad i = 1,\dots,m \\ &&&h_j(x) = 0, \quad j = 1, \dots,p \end where * is the objective function to be minimized over the -variable vector , * are cal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fairness Criteria
Fairness or being fair can refer to: * Justice * The character in the award-nominated musical comedy '' A Theory of Justice: The Musical.'' * Equity (law), a legal principle allowing for the use of discretion and fairness when applying justice * Social justice, equality and solidarity in a society * Distributive justice, the perceived appropriateness of the distribution of goods, benefits, and other outcomes in a society, group, or organization (see also: teleology) * Procedural justice, the perceived appropriateness of rules or procedures used to allocate goods, benefits, and other outcomes (see also: deontology) * Interactional justice, the perceived appropriateness of interpersonal treatment * Environmental justice, the perceived appropriateness of the use or treatment of the environment or people via the environment, typically as a function of interpersonal or international relations * Fairness measure, metrics to quantify the fair distribution of resources * Perc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Branch And Bound
Branch and bound (BB, B&B, or BnB) is an algorithm design paradigm for discrete and combinatorial optimization problems, as well as mathematical optimization. A branch-and-bound algorithm consists of a systematic enumeration of candidate solutions by means of state space search: the set of candidate solutions is thought of as forming a rooted tree with the full set at the root. The algorithm explores ''branches'' of this tree, which represent subsets of the solution set. Before enumerating the candidate solutions of a branch, the branch is checked against upper and lower estimated ''bounds'' on the optimal solution, and is discarded if it cannot produce a better solution than the best one found so far by the algorithm. The algorithm depends on efficient estimation of the lower and upper bounds of regions/branches of the search space. If no bounds are available, the algorithm degenerates to an exhaustive search. The method was first proposed by Ailsa Land and Alison Doig whil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Constraint Satisfaction Problem
Constraint satisfaction problems (CSPs) are mathematical questions defined as a set of objects whose state must satisfy a number of constraints or limitations. CSPs represent the entities in a problem as a homogeneous collection of finite constraints over variables, which is solved by constraint satisfaction methods. CSPs are the subject of research in both artificial intelligence and operations research, since the regularity in their formulation provides a common basis to analyze and solve problems of many seemingly unrelated families. CSPs often exhibit high complexity, requiring a combination of heuristics and combinatorial search methods to be solved in a reasonable time. Constraint programming (CP) is the field of research that specifically focuses on tackling these kinds of problems. Additionally, Boolean satisfiability problem (SAT), the satisfiability modulo theories (SMT), mixed integer programming (MIP) and answer set programming (ASP) are all fields of research f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
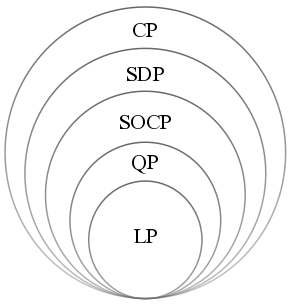
Convex Programming
Convex optimization is a subfield of mathematical optimization that studies the problem of minimizing convex functions over convex sets (or, equivalently, maximizing concave functions over convex sets). Many classes of convex optimization problems admit polynomial-time algorithms, whereas mathematical optimization is in general NP-hard. Convex optimization has applications in a wide range of disciplines, such as automatic control systems, estimation and signal processing, communications and networks, electronic circuit design, data analysis and modeling, finance, statistics (optimal experimental design), and structural optimization, where the approximation concept has proven to be efficient. With recent advancements in computing and optimization algorithms, convex programming is nearly as straightforward as linear programming. Definition A convex optimization problem is an optimization problem in which the objective function is a convex function and the feasible set ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Programming
Linear programming (LP), also called linear optimization, is a method to achieve the best outcome (such as maximum profit or lowest cost) in a mathematical model whose requirements are represented by linear relationships. Linear programming is a special case of mathematical programming (also known as mathematical optimization). More formally, linear programming is a technique for the optimization of a linear objective function, subject to linear equality and linear inequality constraints. Its feasible region is a convex polytope, which is a set defined as the intersection of finitely many half spaces, each of which is defined by a linear inequality. Its objective function is a real-valued affine (linear) function defined on this polyhedron. A linear programming algorithm finds a point in the polytope where this function has the smallest (or largest) value if such a point exists. Linear programs are problems that can be expressed in canonical form as : \begin & \text ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multi-objective Optimization
Multi-objective optimization (also known as multi-objective programming, vector optimization, multicriteria optimization, multiattribute optimization or Pareto optimization) is an area of multiple criteria decision making that is concerned with mathematical optimization problems involving more than one objective function to be optimized simultaneously. Multi-objective optimization has been applied in many fields of science, including engineering, economics and logistics where optimal decisions need to be taken in the presence of trade-offs between two or more conflicting objectives. Minimizing cost while maximizing comfort while buying a car, and maximizing performance whilst minimizing fuel consumption and emission of pollutants of a vehicle are examples of multi-objective optimization problems involving two and three objectives, respectively. In practical problems, there can be more than three objectives. For a nontrivial multi-objective optimization problem, no single soluti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Network Flow Problem
In combinatorial optimization, network flow problems are a class of computational problems in which the input is a flow network (a graph with numerical capacities on its edges), and the goal is to construct a flow, numerical values on each edge that respect the capacity constraints and that have incoming flow equal to outgoing flow at all vertices except for certain designated terminals. Specific types of network flow problems include: *The maximum flow problem, in which the goal is to maximize the total amount of flow out of the source terminals and into the sink terminals *The minimum-cost flow problem, in which the edges have costs as well as capacities and the goal is to achieve a given amount of flow (or a maximum flow) that has the minimum possible cost *The multi-commodity flow problem, in which one must construct multiple flows for different commodities whose total flow amounts together respect the capacities * Nowhere-zero flow, a type of flow studied in combinatorics in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |